Rotating Sweep Line Technique (Bulldozer Trick)

본 글은 JusticeHui 님의 Rotating Sweep Line Technique (Bulldozer Trick)을 보고 개인 공부의 목적으로 작성한 글입니다.

서론

데이터가 정렬되어 있다는 것은 문제를 풀 때 굉장히 많은 도움이 된다.

모든 원소가 다른 배열에서 $A_i$보다 작은 가장 큰 원소와 같은 질의를 단순히 $A_{i-1}$을 반환하는 것으로 해결할 수 있다.

데이터가 정수와 같이 순서가 자명하다면 단순히 정렬하면 되지만, 2차원상의 점이라면 어떤 축을 기준으로 보느냐에 따라 정렬의 결과가 달라질 수 있다.

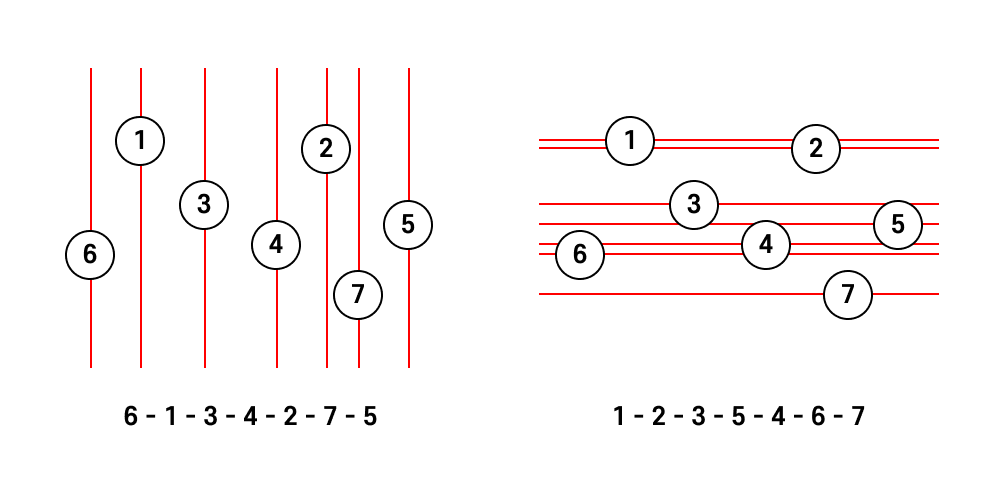
흔히 Rotating Sweep Line Technique, 불도저 트릭이라고 불리는 이 테크닉은 위와 같이 서로 다른 정렬의 결과가 $O(N^2)$가지임을 보이고, 가능한 모든 정렬 결과를 $O(N^2 \log N)$에 순회하는 테크닉이다.

정렬의 경우의 수

보통 점$(x_i, y_i)$을 정렬하라고 하면 $x$좌표 오름차순으로 정렬한다.

이 정렬 방법은 $y$축에 평행한 직선(기울기가 $\infin$인 직선)이 왼쪽부터 오른쪽으로 차례대로 이동하면서 만나는 점들에 순서대로 번호를 붙이는 것과 동일하다.

마찬가지로 $y$좌표 내림차순으로 정렬하는 것은 $x$축에 평행한 직선(기울기가 $0$인 직선)이 한 방향으로 이동하면서 만나는 점들에 순서대로 번호를 붙이는 것과 같다.

따라서 서로 다른 정렬의 결과가 $O(N^2)$가지임을 보이는 것은, 유효한 정렬 기준 기울기가 $O(N^2)$개밖에 없다는 것을 보이면 된다.

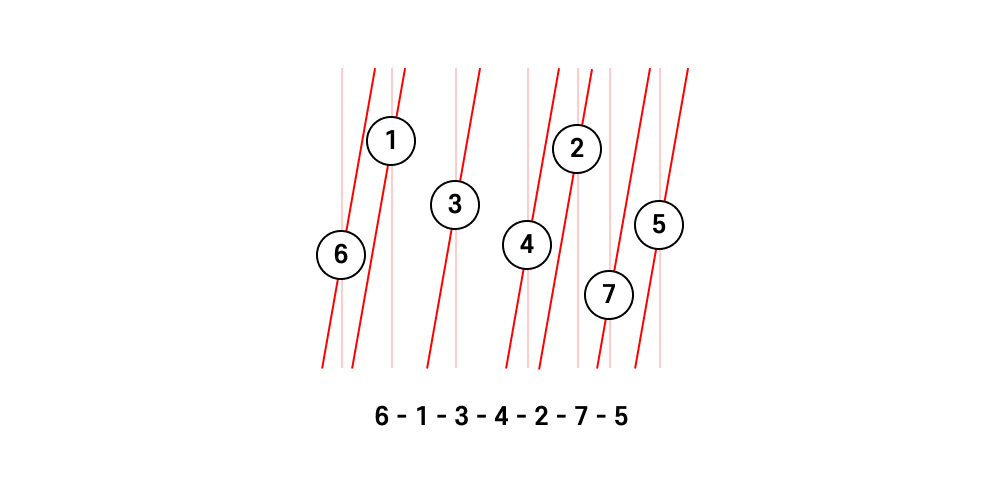
정렬 기준 기울기를 미세하게 변화시키더라도 정렬 결과는 바뀌지 않음을 직관적으로 알 수 있다.

위 그림은 빨간색 직선을 시계방향으로 10도 회전한 것이다.

시계방향으로 계속 회전시키다 보면 1번 점과 6번 점을 잇는 선분과 평행해지는 시점에 1번 점과 6번 점의 순위가 동등해진다.

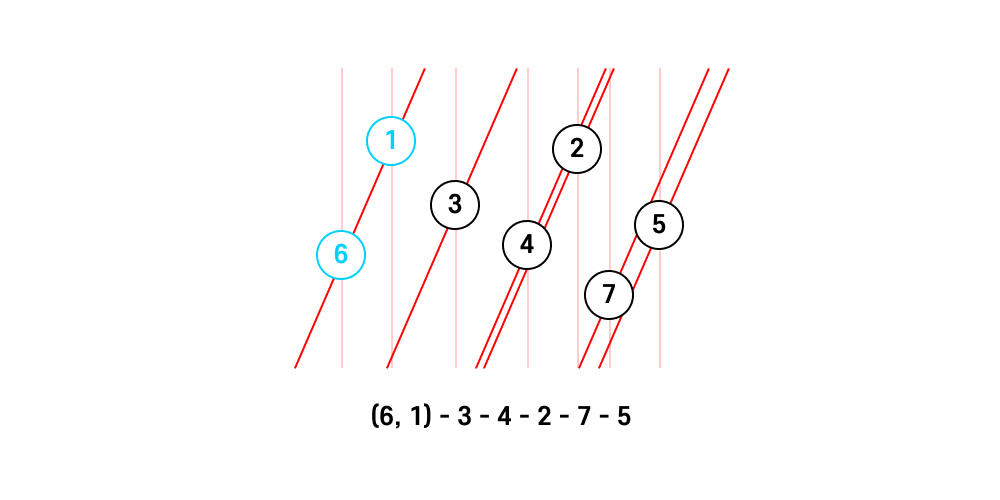
이 상황에서 시계방향으로 아주 조금 더 돌리면 $x$좌표가 더 큰 점(1번 점)이 앞에 오고, $x$좌표가 더 작은 점(6번 점)이 뒤로 오게 된다.

따라서 두 점을 잇는 선분의 기울기만 봐도 모든 정렬의 결과를 알 수 있으므로, 가능한 정렬 결과의 경우의 수는 $O(N^2)$가지이다.

활용

구현 방법은 뒤에서 살펴보고, 이 테크닉을 어디에 활용할 수 있는 지 먼저 알아보자.

9484. 최대삼각형, 최소 삼각형

간단히 문제를 보면 $N$개의 점이 주어졌을 때, 3개의 점을 이용해서 만들 수 있는 삼각형 중 넓이의 최댓값과 최솟값을 구하는 문제다.

Naive하게 생각해보면 $O(N^3)$에 해당하는 모든 삼각형의 넓이를 외적을 통해서 구한 뒤 비교하면 된다.

이런 문제라면 Diamond 3이 붙을 이유가 없지만 $N \leq 2000$ 이라는 조건때문에 당연히 불가능하다.

삼각형의 넓이는 밑변과 길이의 곱을 2로 나눠서 구할 수 있다. 만약 밑변으로 사용할 두 꼭짓점을 고정한다면, 두 꼭짓점을 잇는 직선과 가장 가까운 점을 선택하면 최소 넓이 삼각형을 얻을 수 있다.

마찬가지로 직선과 가장 먼 점을 선택하면 최대 넓이를 얻을 수 있다.

이 문제는 Rotating Sweep Line Technique을 이용해 해결할 수 있다.

두 점을 잇는 선분의 기울기를 기준으로 정렬했고, 두 점의 번호를 각각 $u, v (u<v)$라고 하자.

그럼 가장 가까운 점은 $u-1, v+1$ 중 하나이며, 가장 먼 점은 $1, N$ 중 하나일 것이다.

따라서 단순히 점들의 정렬 순서만 관리해주면 이 문제를 해결할 수 있다.

연습 문제

• BOJ 3121. 빨간점, 파란점
• BOJ 16783. Bulldozer
• BOJ 17625. 고압선
• BOJ 17973. Quadrilaterals

References

• Rotating Sweep Line Technique (Bulldozer Trick)