
06. 미로 찾기 문제
입구에서 출구로 통하는 길을 찾는 미로 찾기 문제
스택을 활용하여 문제를 해결할 수 있음
출구 탐색을 위해 BFS나 DFS로 해결할 수 있음
아래 그림에서 Enter 에서 Exit을 찾아가는 path의 좌표를 출력하세요
움직 일 수 있는 방향의 예: ( 2,2 ) 위치에서 볼 수 있는 도달 가능 위치는 N(2,1), E(3,2), S(2,3), W(1,2)
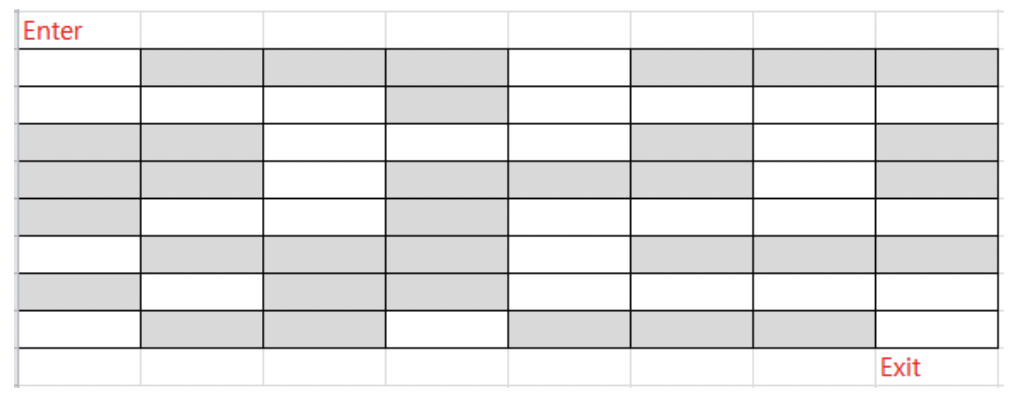
하나의 위치를 방문할때마다 stack에 위치를 저장 (push)
저장된 위치에서 더 이상 갈 곳이 없는 경우 되돌아 간다. ( pop )
stack에서 꺼낸 위치에서 가지 않은 곳을 찾아 간다.
미로 정의
public class Maze {
public int[][] myMaze ={
{0, 1, 1, 1, 0, 1, 1, 1},
{0, 0, 0, 1, 0, 0, 0, 0},
{1, 1, 0, 0, 0, 1, 0, 1},
{1, 1, 0, 1, 1, 1, 0, 1},
{1, 0, 0, 1, 0, 0, 0, 0},
{0, 1, 1, 1, 0, 1, 1, 1},
{1, 0, 1, 1, 0, 0, 0, 0},
{0, 1, 1, 0, 1, 1, 1, 0}
};
}
움직이는 위치
public class Move {
int direction=0;
public int x=0;
public int y=0;
public Move(int x,int y){
this.x = x;
this.y = y;
}
}움직임을 표시할 변수(Robot.java)
public static int NUMDIRECTIONS = 4;
// 미로 크기
public static int WIDTH = 8;
public static int HEIGHT = 8;
Stack<Move> stack = new Stack<Move>();
Move Move;
Maze maze = new Maze();
public int[][] DIRECTION_OFFSETS =
{
// 이것을 MOVE 좌표에 적용 해줌
{0, -1}, // 위쪽으로 이동.
{1, 0}, // 오른쪽으로 이동.
{0, 1}, // 아래쪽으로 이동.
{-1, 0} // 왼쪽으로 이동.
};
public static int NOTVISIT = 0;
public static int WALL = 1;
public static int VISIT = 2;
int[][] markArray = new int[8][8];
출구 찾기
public void findPath( int startX, int startY, int endX, int endY) {
boolean isEmpty = false;
boolean isFound = false;
int i = 0;
Move start = new Move(startX, startY);
start.direction = 0;
stack.push(start);
while(isEmpty == false && isFound == false) {
Move curPos = stack.pop();
int x = curPos.x;
int y = curPos.y;
int direction = curPos.direction;
while(isFound == false && direction < NUMDIRECTIONS) {
int newX = x + DIRECTION_OFFSETS[direction][0];
int newY = y + DIRECTION_OFFSETS[direction][1];
// 갈만한 곳이 있으면 new position 으로 업데이트
if (newX >= 0 && newX < WIDTH
&& newY >= 0 && newY < HEIGHT
&& maze.myMaze[newY][newX] == NOTVISIT
&& markArray[newY][newX] == NOTVISIT) {
Move newPosition = new Move(newX, newY);
newPosition.direction = direction + 1;
stack.push(newPosition);
markArray[y][x] = VISIT;
x = newX;
y = newY;
direction = 0;
if (newX == endX && newY == endY) {
isFound = true;
newPosition.x = newX;
newPosition.y = newY;
newPosition.direction = 0;
stack.push(newPosition);
markArray[newY][newX] = VISIT;
}
}
else direction++;
}//end-of-while
isEmpty = stack.isEmpty();
}//end-of-while
}
찾은 길 출력
public void showPath() {
int[][] resultArray = new int[8][8];
boolean isEmpty = false;
for(int i = 0; i < HEIGHT; i++) {
for(int j = 0; j < WIDTH; j++) {
resultArray[i][j] = maze.myMaze[i][j];
}
}
for(int i = 0; i < HEIGHT; i++) {
for(int j = 0; j < WIDTH; j++) {
if (maze.myMaze[i][j] == WALL) {
System.out.print("*");
}
else if (markArray[i][j] == VISIT) {
System.out.print("|");
}
else {
System.out.print(" ");
}
}
System.out.print("\n");
}
int i = 0;
while(isEmpty == false) {
Move move = stack.pop();
int x = move.x;
int y = move.y;
resultArray[y][x] = VISIT;
if (i > 0) {
System.out.print("<-");
}
System.out.print("(" + x +"," + y + ") ");
i++;
isEmpty = stack.isEmpty();
}
System.out.println();
}
실행
public class MazeTest {
public static void main(String[] args) {
Robot robot;
System.out.println("출구는 입니다. (7,7)");
robot = new Robot();
robot.findPath( 0,0, 7,7);
robot.showPath();
}
}
07.피보나치 수열 문제 여러 방식으로 해결하기
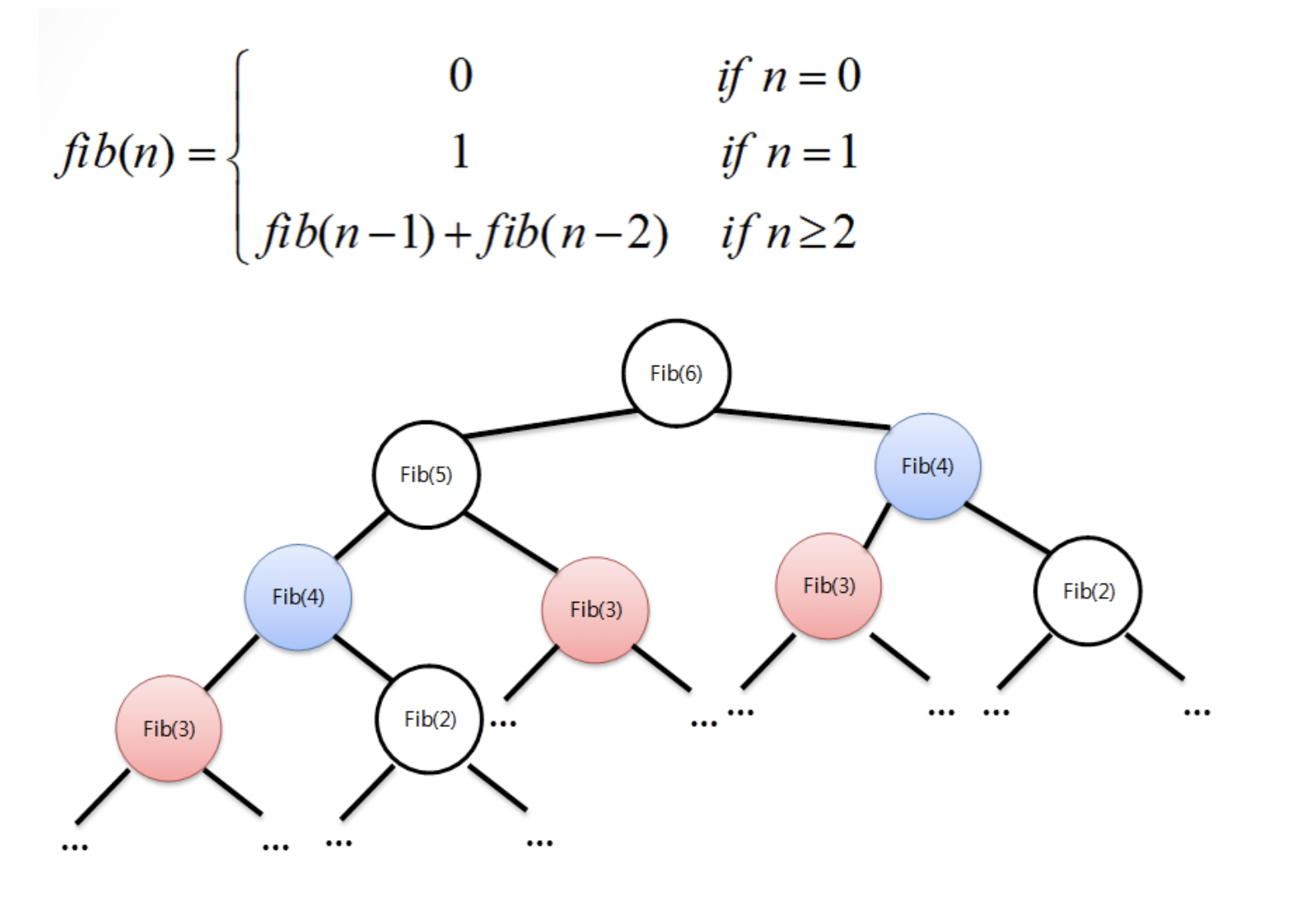
재귀 함수로 풀이하기(O(2^n))
public int fibonacciRecur(int n){
if(n == 0) return 0;
if(n == 1) return 1;
return fibonacciRecur(n-1) + fibonacciRecur(n-2);
}반복문으로 풀기(O(n))
public int fibonacciIteration(int n) {
int ppre = 0;
int pre = 1;
int current = 0;
if (n == 0) return 0;
if (n == 1) return 1;
for (int i = 2; i <= n; i++) {
current = ppre + pre;
ppre = pre;
pre = current;
}
return current;
}
메모이제이션(일종의 동적 프로그래밍)
public int fibonacciMem(int n) {
value[0] = 0;
value[1] = 1;
if (n == 0) {
return value[0];
}
if (n == 1) {
return value[1];
}
int i;
for( i = 2; i<=n; i++) {
value[i] = value[i-1] + value[i-2];
}
return value[i-1];
}
08. 여러 종류의 동전으로 가격 지불하는 문제(Greedy 알고리즘)
다른 용어로 탐욕 알고리즘이라고도 함
지금 상황에서 가장 좋은 해결책을 찾는 알고리즘으로 실제 여러 알고리즘 테스트에서도 흔히 볼 수 있는 문제중 하나임
여러 조합에 따른 그 해를 찾는 경우가 많고 이때 제시되는 대부분의 조건은 "가장 금액이 큰 순서부터" 라던가 "가장 면적이 큰 타일을 우선적으로"등의 방식에 제시
이 알고리즘은 조건이 명확할 때 정확한 답을 찾을 수 있고, 기존의 다른 알고리즘의 지식이 없어도 상식적인 범위에서 코딩이 가능하다.
문제 정의 및 해결
가게에 간 철수는 8370원 어치 물건을 구매하였습니다. 철수에게는 500원짜리 20개 100원짜리 20개 50원짜리 20개 10원짜리 20개의 동전이 있습니다. 철수는 금액을 지불 할 때 단위가 큰 동전부터 지불하려고 합니다. 철수가 지불하게 되는 각 동전의 개수를 구하세요
public class GreedyTest {
public static void main(String[] args) {
int[] coins = {500, 100, 50, 10}; //
int price = 8370;
int count;
for (int i = 0; i< coins.length; i++) {
count = 0;
count += price / coins[i];
price = price % coins[i];
System.out.println( coins[i] + "짜리 동전 " + count + "가 필요합니다.");
}
}
}
09. 경우의 수 문제 (Brute-Force Search)
모든 경우에 대하여 탐색하여 결과를 찾는 문제
문제의 범위가 간단한 경우 완전 탐색으로 모든 해를 찾아보는 방식
수학에서 수열이나 조합과 같은 문제를 해결하는데 사용
심각한 인플레이션을 겪고 있는 어느나라에서 1만원, 2만원, 5만원, 10만원 20만원 50만원 여섯가지 지폐를 사용하고 있다.
배고파씨는 100만원 어치 빵을 사려고 마트에 가서 돈을 내려다 여섯 가지 지폐를 이용하여 100만원 어치 빵을 사는 방법이 모두 몇 가지인지궁금해 졌다.
지불하는 방법은 모두 몇 가지가 있을까?
예를 들어 1만원 10장, 10만원 4장, 50만원 1장 으로 100만원을 지불 할 수 있다.
모두 몇가지인지 구하세요100 만원이 되는 모든 경우에 대해 탐색하여 지불 가능한 경우의 수를 세어본다
public class BruteForceSearch {
public static void main(String[] args) {
int[] bills = { 1, 2, 5, 10, 20, 50 };
int count = 0;
int money = 100;
int i0, i1, i2, i3, i4;
for (i0 = money; i0 >= 0; i0 -= bills[0]) {
for (i1 = i0; i1 >= 0; i1 -= bills[1]) {
for (i2 = i1; i2 >= 0; i2 -= bills[2]) {
for (i3 = i2; i3 >= 0; i3 -= bills[3]) {
for (i4 = i3; i4 >= 0; i4 -= bills[4])
if (i4 % bills[5] == 0)
count++;
}
}
}
}
System.out.println("지불 가능한 가지 수는 : " + count + "가지 입니다.");
}
}
10.특정 범위의 숫자 나열되어 있을 때 각 숫자의 개수를 세어봅시다.
M 이상 N 이하의 수가 나열되어 순서에 상관없이 나열되어 있다고 할 때 각 수가 몇개인지 세어보는 방법을 구현해봅시다.
가령 20세부터 100세 이하의 사람들이 어느 한 장소에 머물고 있다고 할때 연령대에따라 혹은 각 나이에 따른 인원을 체크해볼 수 있습니다.이런 문제의 경우 해결하려는 범위 내에서 counting에 필요한 변수의 개수를 생각해 볼 수 있습니다. 연령대에 따른 경우라면 20대, 30대... 100세 까지 셀 수 있는 변수를 선언해서 증가할 수 있습니다.
그렇지 않고 각 나이마다 counting을 하기 위해서는 그 개수만큼의 변수보다는 배열을 선언하여 개수를 세는 것이 합리적인 방법입니다.
수행에 걸리는 시간은 데이터의 개수가 n개라고 할 때, O(n)입니다.
public class Counting {
public static void main(String[] args) {
int[] people = { 55, 40, 27, 99, 76, 81, 29, 31,33, 62};
int[] ages = new int[10]; //연령대에 따른 수 세기
for(int i = 0; i<people.length; i++) {
int age = people[i];
if(age <30) ages[0]++;
else if(age < 40) ages[1]++;
else if(age < 50) ages[2]++;
else if(age < 60) ages[3]++;
else if(age < 70) ages[4]++;
else if(age < 80) ages[5]++;
else if(age < 90) ages[6]++;
else if(age <= 100) ages[7]++;
}
int number = people.length;
System.out.println( number + "명 중 20대는 " + ages[0]+ "명 입니다.");
System.out.println( number + "명 중 30대는 " + ages[1]+ "명 입니다.");
System.out.println( number + "명 중 40대는 " + ages[2]+ "명 입니다.");
System.out.println( number + "명 중 50대는 " + ages[3]+ "명 입니다.");
System.out.println( number + "명 중 60대는 " + ages[4]+ "명 입니다.");
System.out.println( number + "명 중 70대는 " + ages[5]+ "명 입니다.");
System.out.println( number + "명 중 80대는 " + ages[6]+ "명 입니다.");
System.out.println( number + "명 중 90대는 " + ages[7]+ "명 입니다.");
}
}
