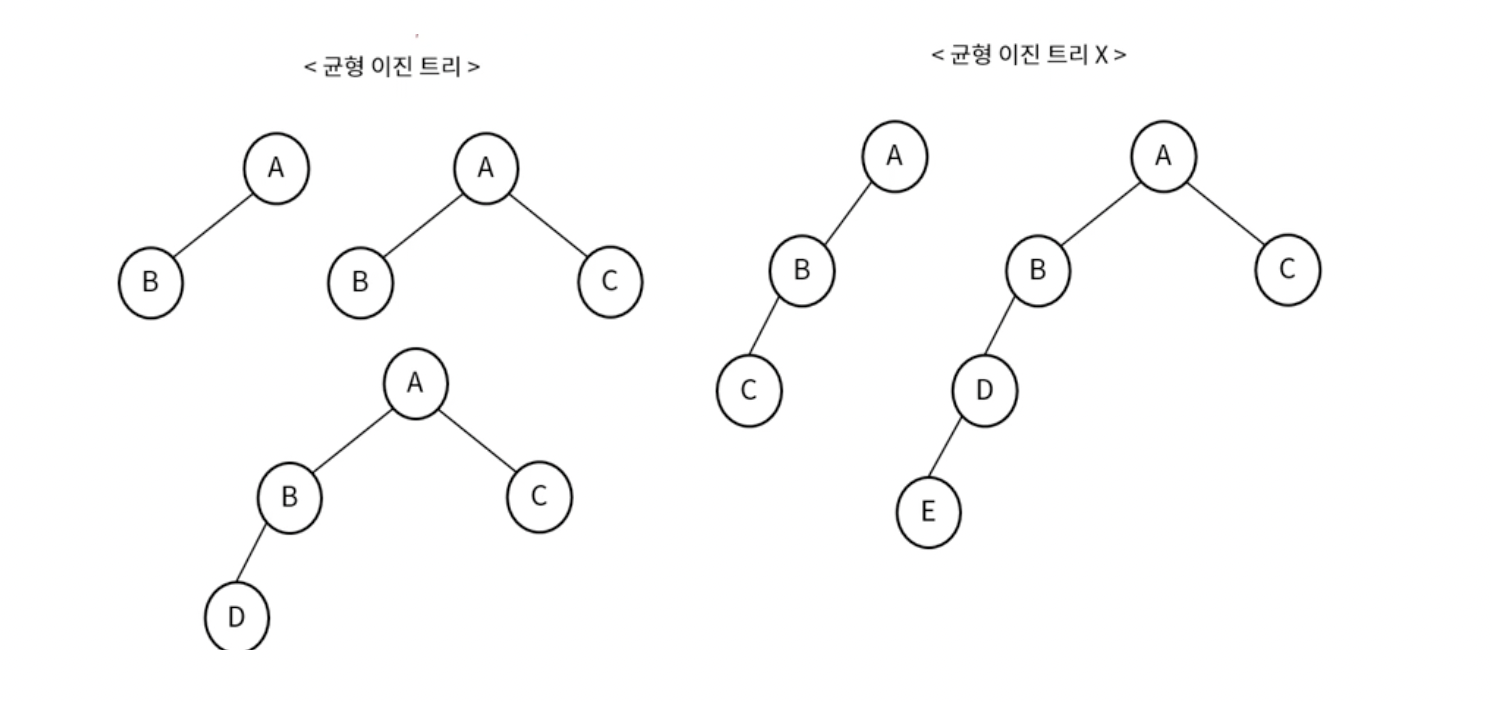
균형 이진 트리에 대해 자세히 알아보기! (비선형 자료구조)

WOOK JONG KIM·2023년 3월 12일
zb_자료구조&알고리즘
0

zb_자료구조&알고리즘

목록 보기
15/31
post-thumbnail

균형 이진 트리

모든 노드의 좌우 서브 트리 높이가 1이상 1이상 차이 나지 않는 트리

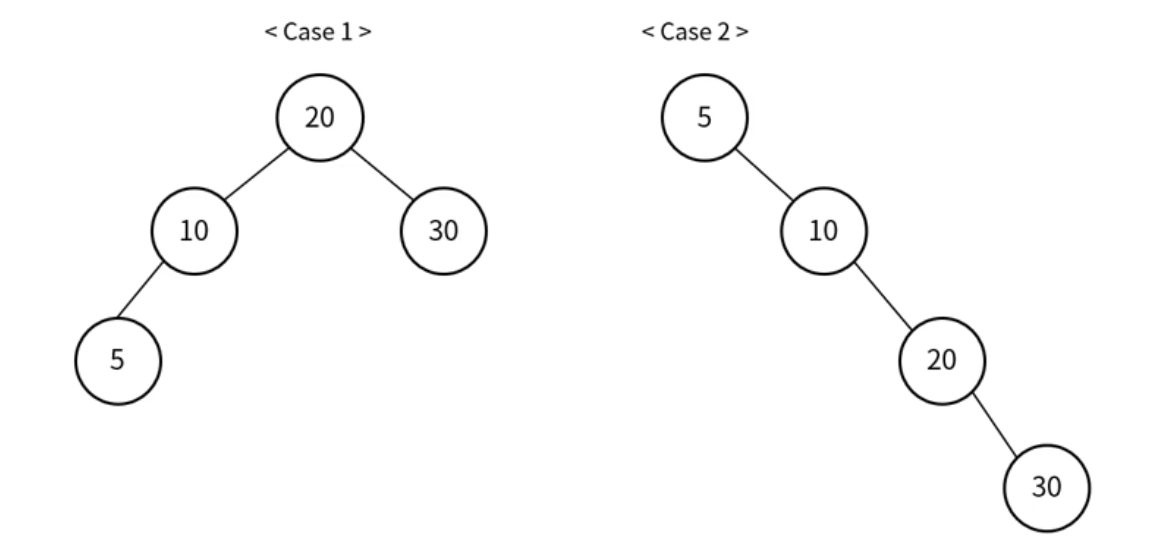
케이스 1 : 이진 탐색 트리에 삽입되는 순서 -> 20, 10, 30, 5 (편향 발생 X)
케이스 2. 이진 탐색 트리에 삽입되는 순서 -> 5, 10, 20, 30 (편향 발생)

균형 이진 탐색 트리

Balanced Binary Search Tree

노드의 삽입과 삭제가 일어날 때 균형을 유지하도록 하는 트리

대표적으로 AVL트리, Red-black 트리

AVL 트리

노드가 삽입,삭제 될 때 트리의 균형을 체크하고 유지하는 트리

BF(Balance Factor) : 왼쪽 서브 트리 높이 - 오른쪽 서브 트리 높이
-> 각 노드의 BF를 [-1,0,1]만 가지게 하여 균형 유지

AVL 트리 리밸런싱

균형이 꺠진 경우
-> BF가 +이면 왼쪽 서브 트리에 이상이 있음
-> BF가 -이면 오른쪽 서브 트리에 이상이 있음

회전 연산
-> 단순 회전 - LL, RR
-> 이중 회전 - LR, RL

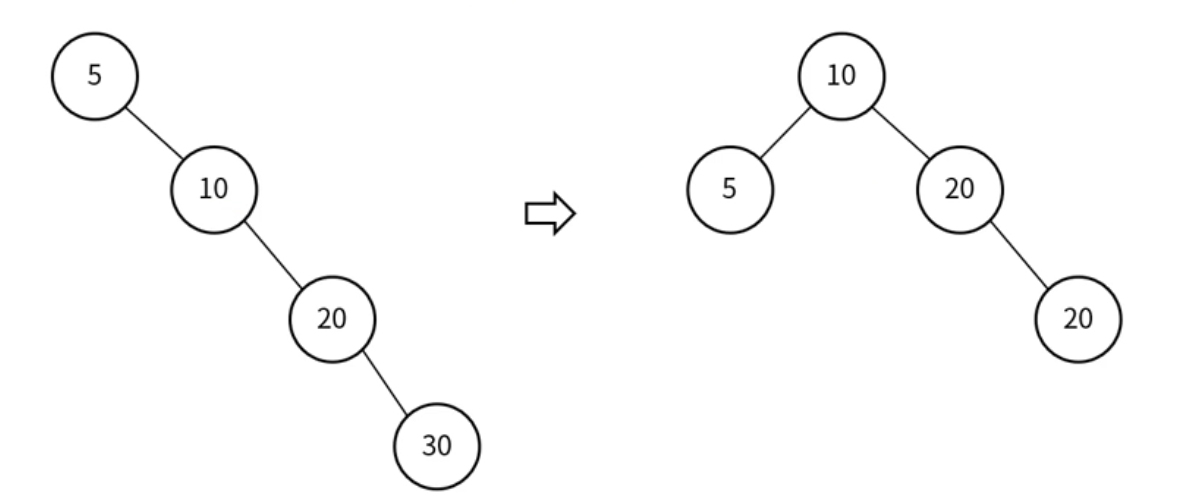
LL(Left-Left)

회전 1회, 오른쪽 방향으로 회전

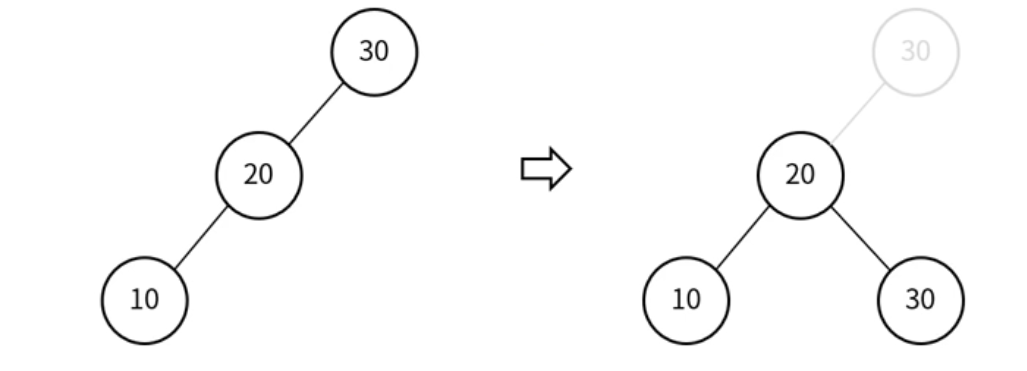
RR(Right-Right)

회전 1회, 왼쪽 방향으로 회전

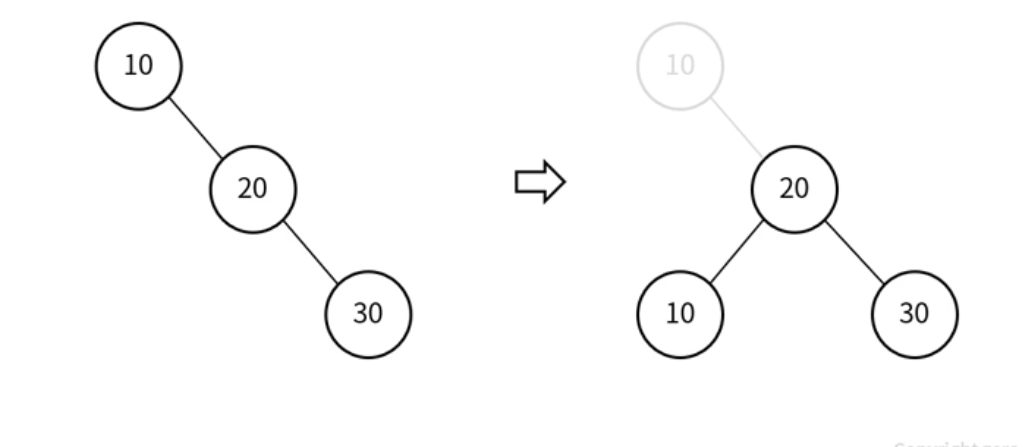
LR(Left-Right)

회전 2회, RR 회전 후 LL 회전

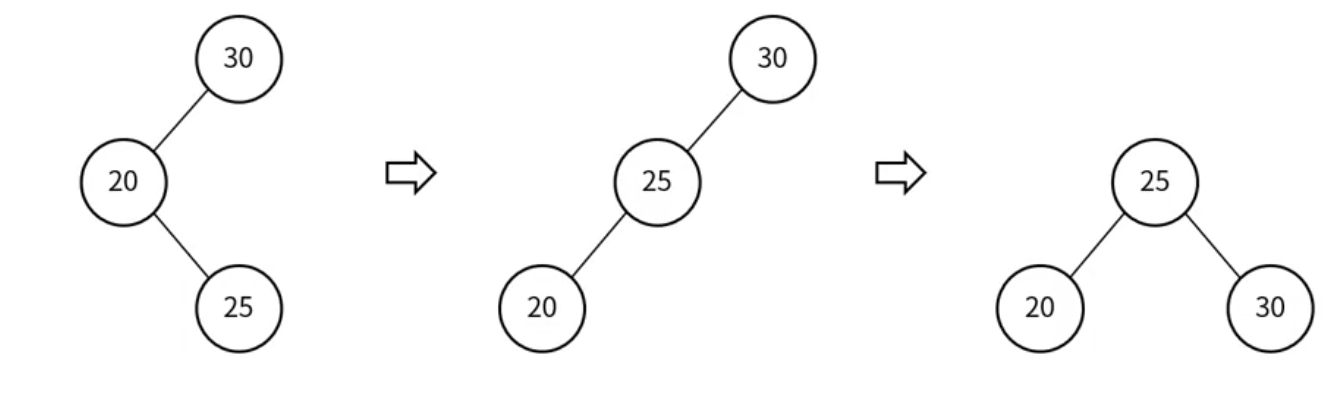
RL(Right-Left)

회전 2회, LL 회전 후 RR 회전

AVL 트리 구현

삽입

// AVL 트리

import java.util.LinkedList;
import java.util.Queue;

class Node{
    int key;
    int height; // 현재 노드의 높이
    Node left;
    Node right;

    public Node(int key,  Node left, Node right) {
        this.key = key;
        this.height = 0;
        this.left = left;
        this.right = right;
    }
}

class AVLTree{
    Node head;

    public int height(Node node){
        if(node == null){
            return -1;
        }
        return node.height;
    }

    public Node rightRotate(Node node){
        Node lNode = node.left;

        node.left = lNode.right;
        lNode.right = node;

        node.height = Math.max(height(node.left), height(node.right)) + 1;
        lNode.height = Math.max(height(lNode.left), height(lNode.right)) + 1;

        return lNode;
    }

    public Node leftRotate(Node node){
        Node rNode = node.right;

        node.right = rNode.left;
        rNode.left = node;

        node.height = Math.max(height(node.left), height(node.right)) + 1;
        rNode.height = Math.max(height(rNode.left), height(rNode.right)) + 1;

        return rNode;
    }

    public Node lrRotate(Node node){
        node.left = leftRotate(node.left);
        return rightRotate(node);
    }

    public Node rlRotate(Node node){
        node.right = rightRotate(node.right);
        return leftRotate(node);
    }

    public int getBalance(Node node){
        if(node == null){
            return 0;
        }
        return height(node.left) - height(node.right);
    }

    public void insert(int key){
        this.head = insert(this.head, key);
    }

    public Node insert(Node node, int key){
        if(node == null){
            return new Node(key, null, null);
        }

        if(key < node.key){
            node.left = insert(node.left, key);
        }else{
            node.right = insert(node.right, key);
        }

        node.height = Math.max(height(node.left), height(node.right)) + 1;

        int balance = getBalance(node);

        // LL인 경우
        if(balance > 1 && key < node.left.key){
            return rightRotate(node);
        }

        // RR인 경우
        if(balance < 1 && key > node.right.key){
            return leftRotate(node);
        }

        // LR인 경우
        if(balance > 1 && key > node.left.key){
            return lrRotate(node);
        }

        if(balance < 1 && key < node.right.key){
            return rlRotate(node);
        }

        return node;
    }

    public void levelOrder(Node node){
        Queue<Node> queue = new LinkedList<>();
        queue.add(node);
        while(!queue.isEmpty()){
            Node cur = queue.poll();

            System.out.print(cur.key + " ");
            if(cur.left != null){
                queue.offer(cur.left);
            }
            if(cur.right != null){
                queue.offer(cur.right);
            }
        }
        System.out.println();
    }
}
public class Practice1 {
    public static void main(String[] args) {
        AVLTree avl = new AVLTree();

        avl.insert(30);avl.insert(20);avl.insert(10);
        avl.levelOrder(avl.head); // LL

        avl.insert(40);avl.insert(50);
        avl.levelOrder(avl.head); // RR

        avl.insert(5); avl.insert(7);
        avl.levelOrder(avl.head); // LR

        avl.insert(60);
        avl.insert(55);
        avl.levelOrder(avl.head); // RL
    }
}

삭제

class AVLTree2 extends AVLTree{
    public void delete(int key){
        this.head = delete(this.head, key);
    }

    public Node delete(Node node, int key){
        if(node == null){
            return null;
        }
        
        if(key < node.key){
            node.left = delete(node.left, key);
        }else if(key > node.key){
            node.right = delete(node.right, key);
        }else{
            if(node.left == null){
                return node.right;
            }else if(node.right == null){
                return node.left;
            }else{
                Node predecessor = node;
                Node successor = node.left;
                
                while(successor.right != null){
                    predecessor = successor;
                    successor = successor.right;
                }
                
                predecessor.right = successor.left;
                node.key = successor.key;
            }
        }
        
        // 높이 갱신
        node.height = Math.max(height(node.left), height(node.right)) + 1;
        
        int balance = getBalance(node);
        
        //LL
        if(balance > 1 && getBalance(node.left) > 0){
            return rightRotate(node);
        }
        //RR
        if(balance < - 1 && getBalance(node.right) < 0){
            return leftRotate(node);
        }
        //LR
        if(balance > 1 && getBalance(node.left) < 0){
            return lrRotate(node);
        }
        //RL
        if(balance < -1 && getBalance(node.right) > 0){
            return rlRotate(node);
        }
        return node;
    }
}

Red-Black 트리

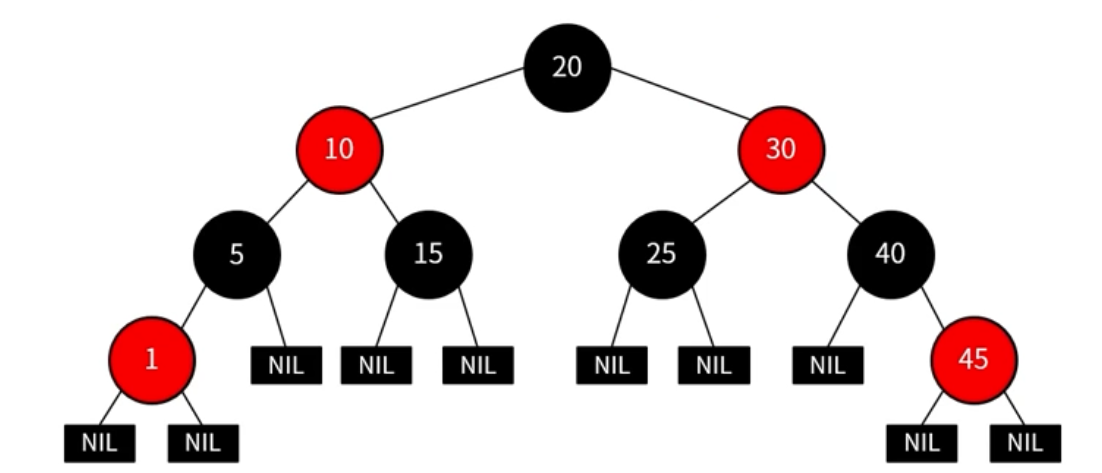
  • 루트 노드와 리프 노드의 색은 black
  • red 색 노드의 자식은 black(double red 불가)
  • 모든 leaf 노드에서 root노드 까지 가는 경로의 black 노드 수는 같음

조건이 꺠지는 상태에서 Rebalancing

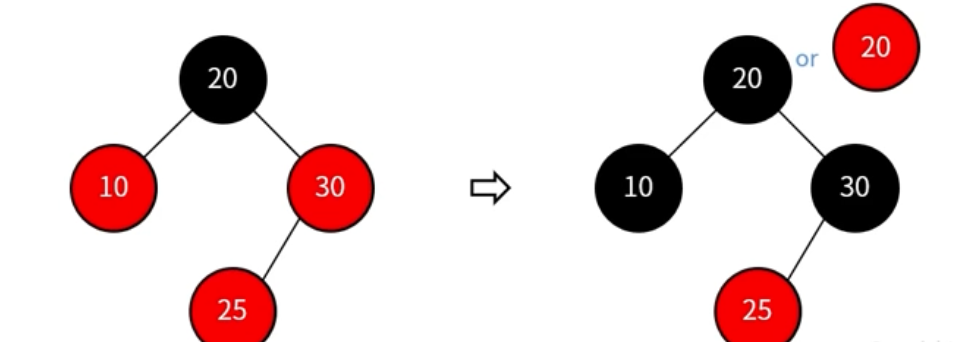
  1. 노드 삽입 후 double red 발생하였는데 (부모 노드의 형제 노드가 red 일때)
    -> Recoloring 진행
    삽입한 노드의 부모와 부모의 형제 노드를 black 으로 변경
    부모의 부모 노드를 red로 변경, 부모의 부모 노드가 root 인지 double red인지에 따라 조정 진행

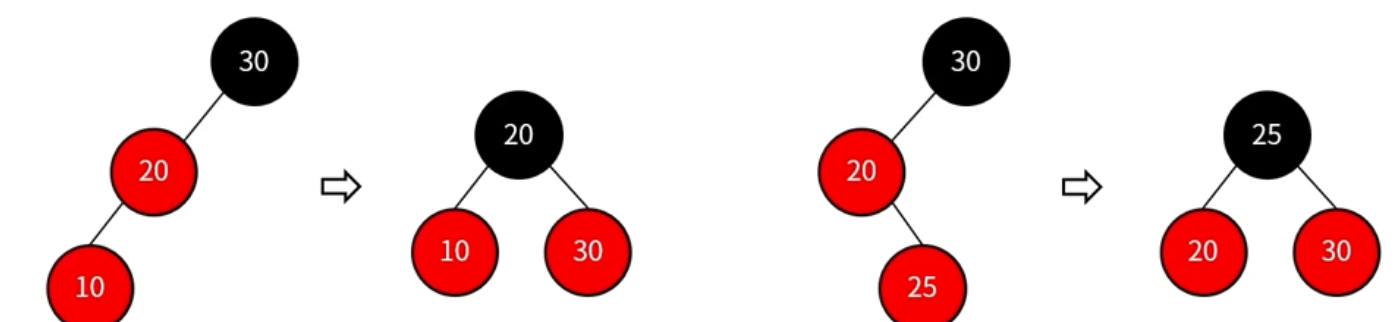
  1. 노드 삽입 후 dobule red 발생(부모 노드의 형제 노드가 black 이거나 없을때)
    -> Restructuring 진행
    조정 대상 : 삽입한 노드, 부모 노드, 부모의 부모 노드
    조정 대상 노드들을 오름차순 정렬
    가운데 노드를 부모 노드로 선정하고 black으로 변경
    나머지 두 노드를 자식 노드로 두고 red로 변경

삭제

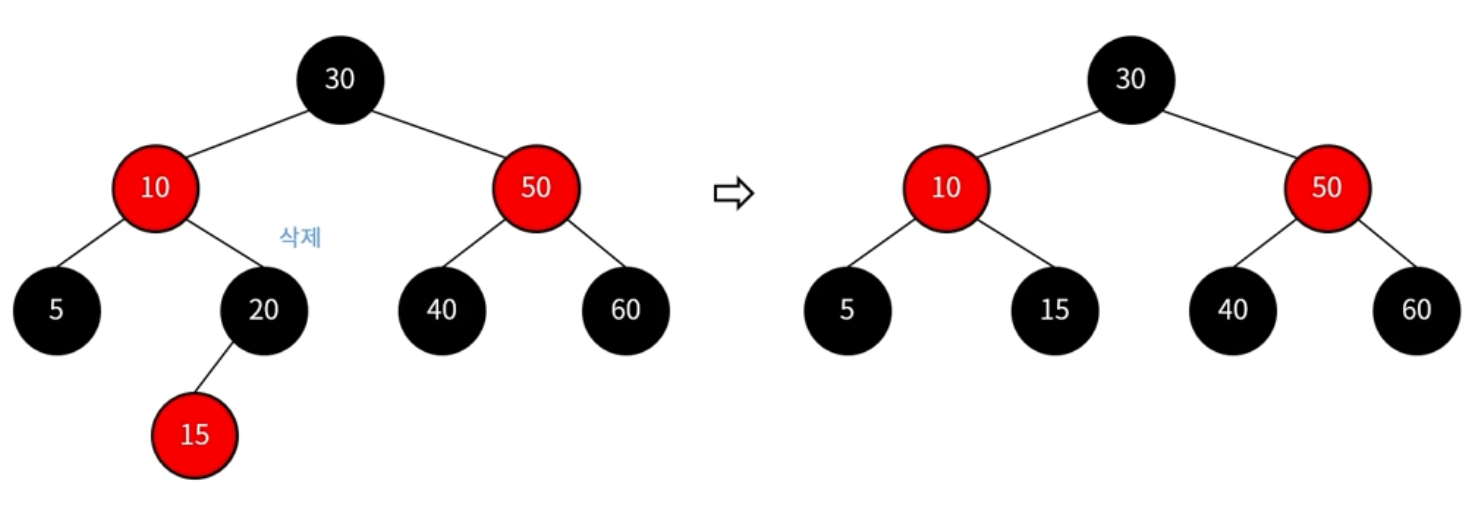
삭제 대상 노드가 black이고, 그자리에 오는 노드가 red인 경우
-> 해당 자리로 오는 red 노드를 black으로 변경

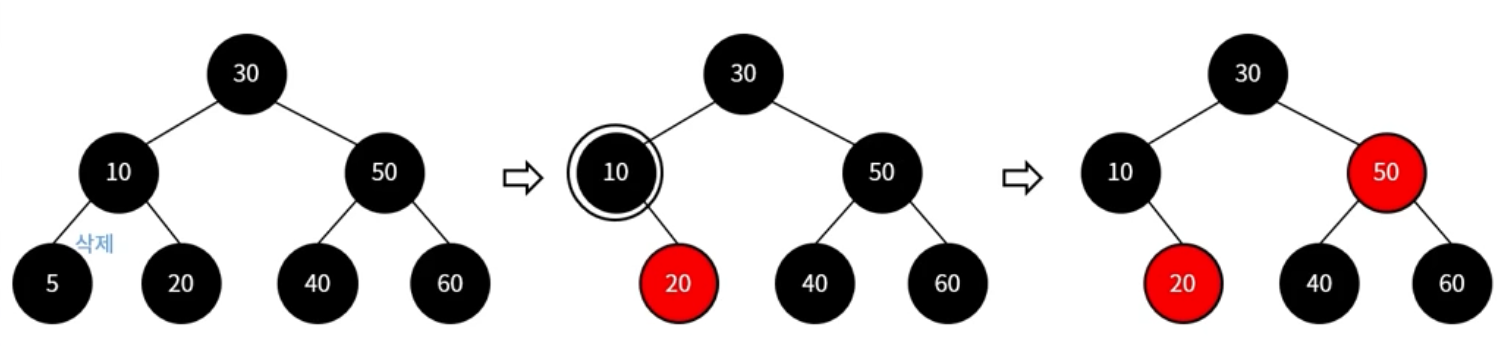
삭제 대상 노드가 black, 그 자리에 오는 노드가 black인 경우

이중 흑색 노드의 형제 노드가 black 이고, 형제의 양쪽 자식 모두 black인 경우
-> 형제 노드를 red로 변경
-> 이중 흑색 노드의 검은색 1개를 부모 노드로 전달
-> 부모가 root가 아닌 이중 흑색 노드가 되면 해당 case 반복 진행

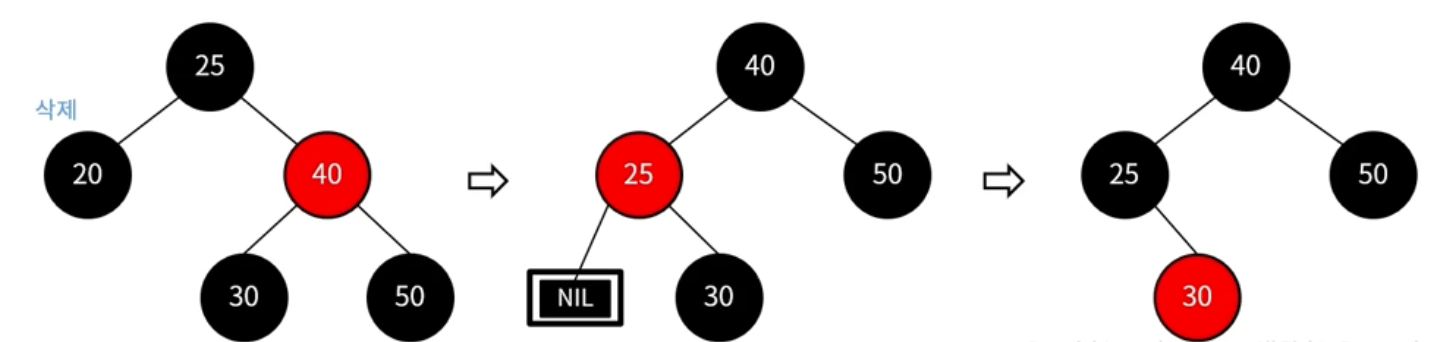
이중 흑색 노드의 형제 노드가 red인 경우
-> 형제 노드를 black으로 변경
-> 부모 노드를 red로 변경
-> 부모 노드를 기준으로 왼쪽으로 회전
-> 그 다음 이중 흑색 case에 따라 반복 진행

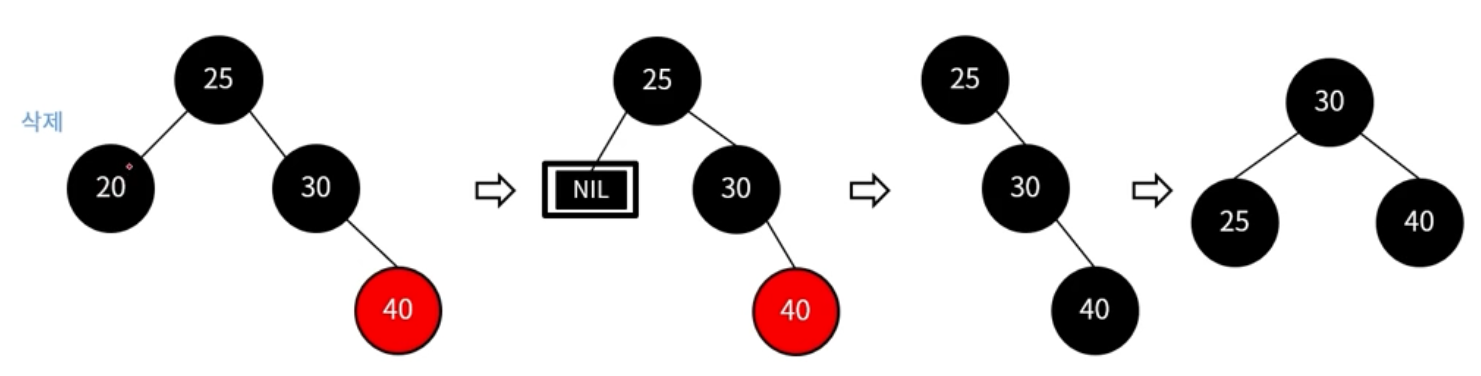
이중 흑색 노드의 형제 노드가 black이고, 오른쪽 자식이 red인 경우
-> 부모 노드와 형제 노드의 오른쪽 자식 노드를 검은색으로 변경
-> 부모 노드를 기준으로 왼쪽으로 회전

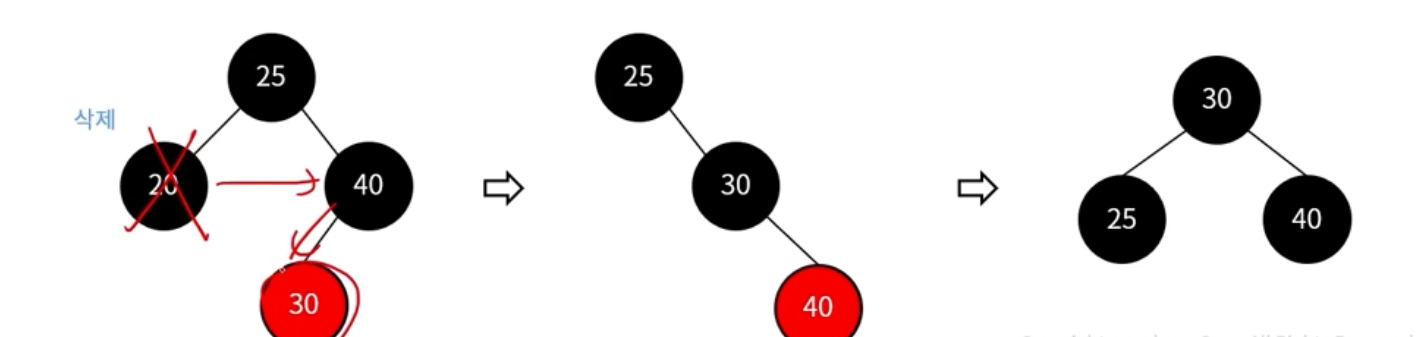
이중 흑색 노드의 형제 노드가 black이고, 왼쪽 자식이 red인 경우
-> 형제 노드를 red로 변경
-> 형제 노드의 왼쪽 자식 노드를 black으로 변경
-> 형제 노드를 기준으로 오른쪽으로 회전

Red-Black 트리 vs AVL 트리

알고리즘 시간 복잡도 -> 둘다 O(logN)

균형 수준 -> AVL 트리가 Red-Black 트리보다 좀 더 엄격하게 균형 잡음

Red-Black 트리는 색으로 구분하는 경우로 인해 회전 수가 감소

실사용시
-> Tree 체계가 잡힌 후, 탐색이 많은 경우에는 AVL 트리가 유리
-> 삽입,삭제가 빈번한 경웬느 Red-Black 트리가 유리

Red-Black 트리 삽입

// 비선형 자료구조 - 이진 탐색 트리_3
// Red-Black 트리 - 삽입

import java.util.LinkedList;
import java.util.Queue;

class Node {
    int key;
    int color;
    Node left;
    Node right;
    Node parent;

    public Node(int key, int color, Node left, Node right, Node parent) {
        this.key = key;
        this.color = color;
        this.left = left;
        this.right = right;
        this.parent = parent;
    }
}

class RedBlackTree {
    static final int BLACK = 0;
    static final int RED = 1;

    Node head;

    public void insert(int key) {
        Node checkNode = null;
        if (this.head == null) {
            // 처음 헤드는 Black
            this.head = new Node(key, BLACK, null, null, null);
        } else {
            Node cur = this.head;

            // 추가할 위치 찾아 추가하는 부분
            while (true) {
                Node pre = cur;

                if (key < cur.key) {
                    // 왼쪽 자식 노드 쪽으로 추가
                    cur = cur.left;
                    if (cur == null) {
                        // 추가할 때는 우선 Red
                        pre.left = new Node(key, RED, null, null, pre);
                        // 추가한 노드를 re-balancing 대상의 노드로 짚어줌
                        checkNode = pre.left;
                        break;
                    }
                } else {
                    cur = cur.right;

                    if (cur == null) {
                        pre.right = new Node(key, RED, null, null, pre);
                        checkNode = pre.right;
                        break;
                    }
                }
            }
            // 추가 후 re-balancing
            reBalance(checkNode);
        }
    }

    public void reBalance(Node node) {
        // 추가한 노드의 부모가 있고 그 부모가 red 일 때 조정 필요
        while (node.parent != null && node.parent.color == RED) {
            Node sibling = null;

            // 부모 노드의 형제 노드 찾기
            if (node.parent == node.parent.parent.left) {
                sibling = node.parent.parent.right;
            } else {
                sibling = node.parent.parent.left;
            }

            // 부모 노드의 형제 노드가 Red 일 때 re-coloring
            if (sibling != null && sibling.color == RED) {
                // 부모 노드 black 으로 변경
                node.parent.color = BLACK;
                // 부모 노드의 형제 노드 black 으로 변경
                sibling.color = BLACK;
                // 부모의 부모 노드는 red 로 변경
                node.parent.parent.color = RED;

                // 부모 노드가 root 인 경우는 다시 black 으로 바꾸고 break
                if (node.parent.parent == this.head) {
                    node.parent.parent.color = BLACK;
                    break;
                } else { // 부모 노드가 root 가 아닌 경우는 double red 재발생 할 수 있으므로 반복 검사
                    node = node.parent.parent;
                    continue;
                }
            } else { // 부모 노드의 형제 없거나 black 일 때, re-structuring
                if (node.parent == node.parent.parent.left) {
                    // lr case 인 경우 우선 ll case 가 되도록 회전
                    if (node == node.parent.right) {
                        node = node.parent;
                        leftRotate(node);
                    }
                    // 부모 노드는 black 으로 변경
                    node.parent.color = BLACK;
                    // 부모의 부모 노드는 red 로 변경
                    node.parent.parent.color = RED;
                    rightRotate(node.parent.parent);
                } else if (node.parent == node.parent.parent.right) {
                    // rl case 인 경우 rr case 가 되도록 회전
                    if (node == node.parent.left) {
                        node = node.parent;
                        rightRotate(node);
                    }
                    node.parent.color = BLACK;
                    node.parent.parent.color = RED;
                    leftRotate(node.parent.parent);
                }
                break;
            }
        }
    }

    public void leftRotate(Node node) {
        // node 가 head 인 경우 회전 후 head 교체
        if (node.parent == null) {
            Node rNode = this.head.right;
            this.head.right = rNode.left;
            rNode.left.parent = this.head;
            this.head.parent = rNode;
            rNode.left = this.head;
            rNode.parent = null;
            this.head = rNode;
        } else {
            // 회전하기 전 자식 노드있는 경우 이동하는 작업
            if (node == node.parent.left) {
                node.parent.left = node.right;
            } else {
                node.parent.right = node.right;
            }
            node.right.parent = node.parent;
            node.parent = node.right;

            if (node.right.left != null) {
                node.right.left.parent = node;
            }
            node.right = node.right.left;
            node.parent.left = node;
        }
    }

    public void rightRotate(Node node) {
        // node 가 head 인 경우 회전 후 head 교체
        if (node.parent == null) {
            Node lNode = this.head.left;
            this.head.left = lNode.right;
            lNode.right.parent = this.head;
            this.head.parent = lNode;
            lNode.right = this.head;
            lNode.parent = null;
            this.head = lNode;
        } else {
            if (node == node.parent.left)
                node.parent.left = node.left;
            else
                node.parent.right = node.left;

            node.left.parent = node.parent;
            node.parent = node.left;

            if (node.left.right != null)
                node.left.right.parent = node;

            node.left = node.left.right;
            node.parent.right = node;
        }
    }

    public void levelOrder(Node node) {
        char[] color = {'B', 'R'};

        Queue<Node> queue = new LinkedList();
        queue.add(node);
        while (!queue.isEmpty()) {
            Node cur = queue.poll();

            System.out.print("[" + color[cur.color] + "]" + cur.key + " ");
            if (cur.left != null) {
                queue.offer(cur.left);
            }

            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
        System.out.println();
    }
}

public class Practice1 {
    public static void main(String[] args) {
        // Test code
        RedBlackTree rbTree = new RedBlackTree();
        rbTree.insert(20);
        rbTree.insert(10);
        rbTree.insert(30);
        rbTree.levelOrder(rbTree.head);
        rbTree.insert(25);
        rbTree.levelOrder(rbTree.head);
        rbTree.insert(5);
        rbTree.insert(7);
        rbTree.levelOrder(rbTree.head);
        rbTree.insert(20);
        rbTree.levelOrder(rbTree.head);
    }
}
profile
WOOK JONG KIM
Journey for Backend Developer
이전 포스트

이진 탐색 트리에 대해 자세히 알아보기! (비선형 자료구조)

다음 포스트

트리 이용한 간단한 응용문제

0개의 댓글