
이진 탐색 트리(Binary Search Tree)
다음과 같은 규칙으로 구성되어있는 이진 트리
- 왼쪽 자식 노드의 키는 부모 노드의 키보다 작음
- 오른쪽 자식 노드의 키는 부모 노드의 키보다 큼
- 각각의 서브 트리도 이진 탐색 트리를 유지
- 중복된 키를 허용하지 않음
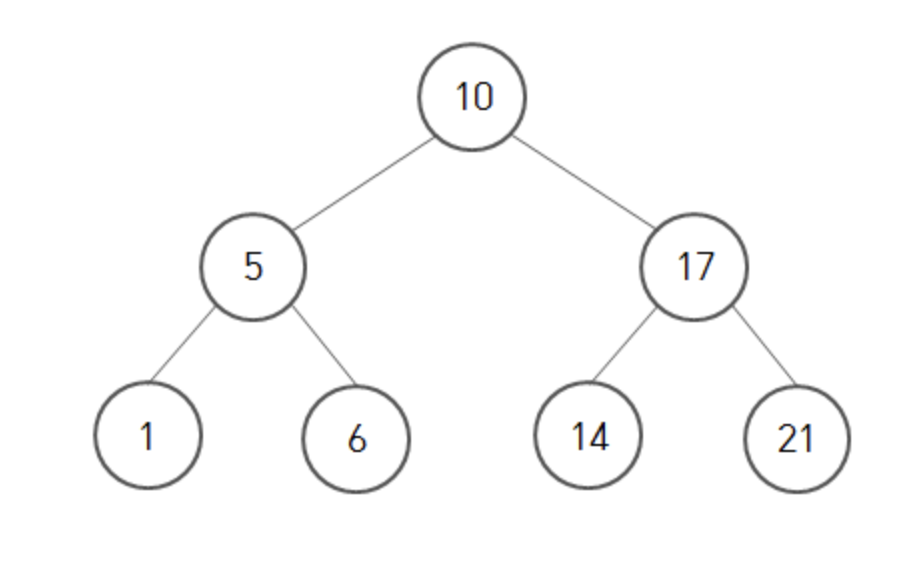
inOrder로 탐색시 오름차순으로 출력됨
이진 트리에 비해 탐색이 빠름(균형 유지 필요!)
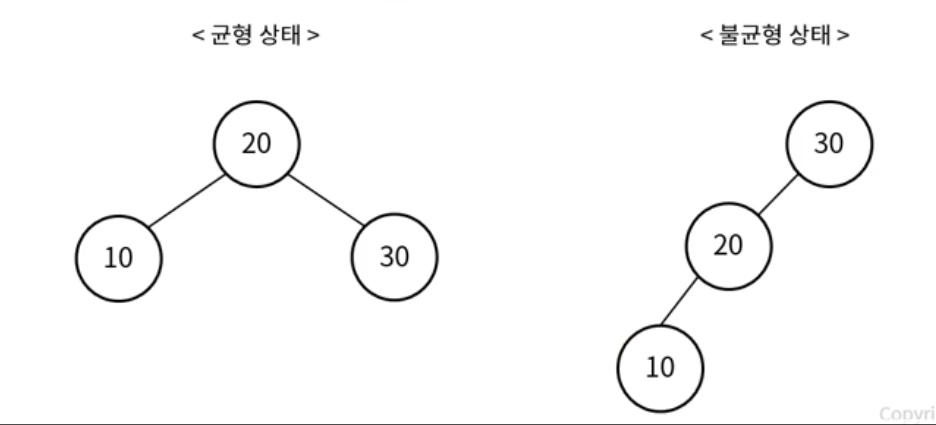
균형 상태 : O(logN) , 불균형 상태 : O(N)
균형 -> 모든 노드의 서브트리 높이 차이가 최대 1인 상태
탐색
탐색 시 찾고자하는 데이터를 루트 노드부터 비교 시작
대소 비교를 하여 찾는 데이터가 작으면 왼쪽, 크면 오른쪽 노드로 이동
찾는 데이터가 없으면 null을 반환하며, 최악의 경우 최대 트리 높이 만큼 탐색이 이루어짐(불균형의 경우 생각)
삽입
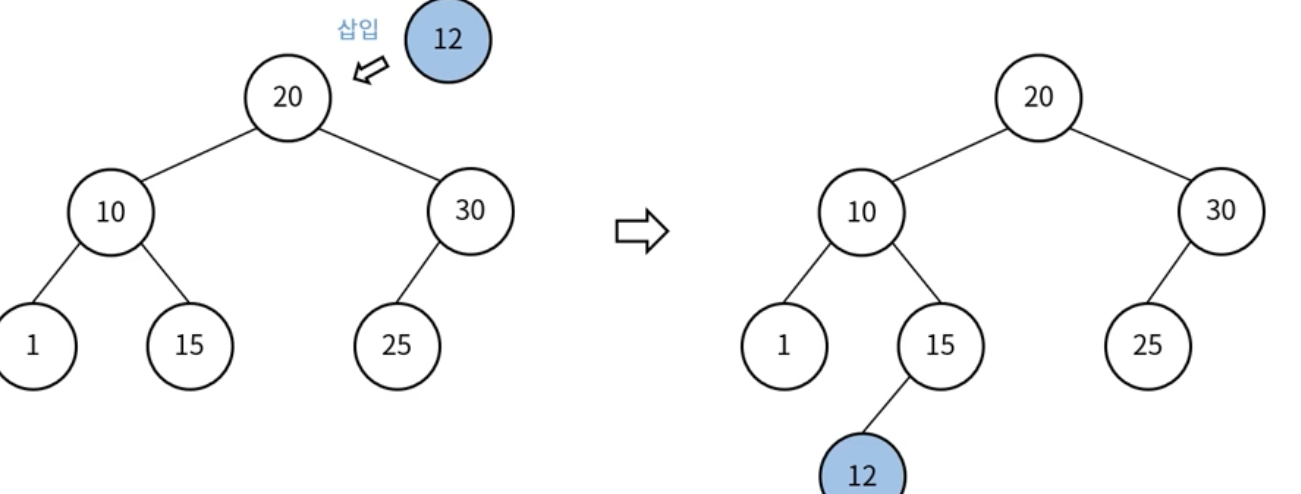
Root부터 비교를 시작하며 중복 키 발견시 노드를 추가하지 않고 종료함
삽입할 키가 현재 노드의 키보다 작으면 왼쪽, 크면 오른쪽으로 이동
Leaf 노드에 도달 후 키를 비교했을 때 작으면 왼쪽, 크면 오른쪽에 삽입
삭제
-
삭제 대상 노드가 Leaf 노드의 경우
삭제 대상 노드를 삭제 후 부모 노드의 해당 자식 링크 null로 변경 -
삭제 대상 노드에 자식 노드가 하나있는 경우
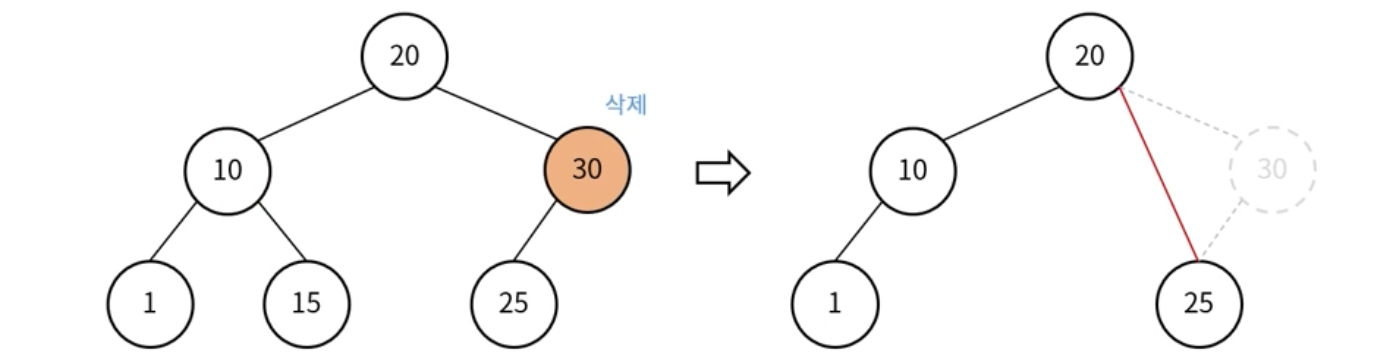
자식 노드를 삭제 대상 노드의 부모 노드에 연결한 후 삭제 대상 노드 삭제
- 삭제 대상 노드에 자식 노드가 둘인 경우
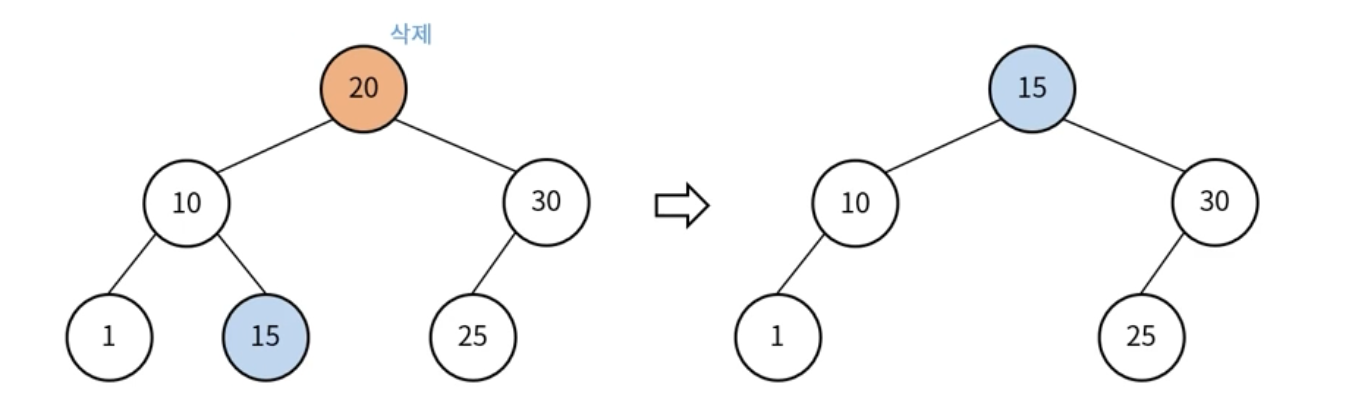
삭제 대상 노드의 왼쪽 서브 트리에서 가장 큰 노드 선택하거나, 삭제 대상 노드의 오른쪽 서브 트리에서 가장 작은 노드를 선택
이후 선택한 노드를 삭제 대상 노드 위치로 올리는데, 올리는 과정에서 다른 자식 노드들의 링크 연결 작업을 진행함
마지막으로 삭제 대상 노드 삭제
이진 탐색 트리 구현해보기
class Node{
int key;
Node left;
Node right;
public Node(int key, Node left, Node right) {
this.key = key;
this.left = left;
this.right = right;
}
}
class BinarySearchTree{
Node head;
public BinarySearchTree(int key) {
this.head = new Node(key, null, null);
}
public void addNode(int key){
if(this.head == null){
this.head = new Node(key, null, null);
}else{
Node cur = this.head;
while(true){
Node pre = cur;
if(key < cur.key){
cur = cur.left;
if(cur == null){
pre.left = new Node(key, null,null);
break;
}
}else{
cur = cur.right;
if(cur == null){
pre.right = new Node(key,null,null);
break;
}
}
}
}
}
public void removeNode(int key){
Node parent = null;
Node successor = null; // 왼쪽 가장 큰거, 오른쪽 가장 작은 거
Node predecessor = null;
Node child = null;
Node cur = this.head;
while(cur != null){
if(key == cur.key){
break;
}
parent = cur;
if(key < cur.key){
cur = cur.left;
}else{
cur = cur.right;
}
}
if(cur == null){
System.out.println("key에 해당하는 노드가 없습니다.");
return;
}
if(cur.left == null && cur.right == null){
// 리프 노드인 경우
if(parent == null){
this.head = null;
}else{
if(parent.left == cur){
parent.left = null;
}else{
parent.right = null;
}
}
} else if(cur.left != null && cur.right == null || cur.left == null && cur.right != null){
// 자식 노드가 하나인 경우
if(cur.left != null){
child = cur.left;
}else{
child = cur.right;
}
if(parent == null){
this.head = child;
}else{
if(parent.left == cur){
parent.left = child;
}else{
parent.right = child;
}
}
} else{
// 자식 노드가 둘인 경우
predecessor = cur;
successor = cur.left;
while(successor.right != null){
predecessor = successor;
successor = successor.right;
}
predecessor.right = successor.left;
successor.left = cur.left;
successor.right = cur.right;
if(parent == null){
this.head = successor;
}else{
if(parent.left == cur){
parent.left = successor;
}else{
parent.right = successor;
}
}
}
}
public void levelOrder(Node node){
Queue<Node> queue = new LinkedList<>();
queue.add(node);
while(!queue.isEmpty()){
Node cur = queue.poll();
System.out.print(cur.key + " ");
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
}
System.out.println();
}
}
public class Practice1 {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree(20);
bst.addNode(10);bst.addNode(30);bst.addNode(1);
bst.addNode(15);bst.addNode(25);bst.addNode(13);
bst.addNode(35);bst.addNode(27);bst.addNode(40);
bst.levelOrder(bst.head);
bst.removeNode(40); bst.levelOrder(bst.head);
bst.removeNode(25); bst.levelOrder(bst.head);
bst.removeNode(20); bst.levelOrder(bst.head);
}
}앞의 BST 삽입, 삭제 코드를 재귀 형태로 구현해보기
import java.util.LinkedList;
import java.util.Queue;
class Node{
int key;
Node left;
Node right;
public Node(int key, Node left, Node right) {
this.key = key;
this.left = left;
this.right = right;
}
}
class BinarySearchTree{
Node head;
public BinarySearchTree(int key) {
this.head = new Node(key, null, null);
}
public Node addNodeRecursive(Node cur, int key){
if(cur == null){
return new Node(key,null,null);
}
if(key < cur.key){
cur.left = addNodeRecursive(cur.left,key);
}else{
cur.right = addNodeRecursive(cur.right, key);
}
return cur;
}
public Node removeNodeRecursive(Node cur, int key){
if(cur == null){
return null;
}
if(key < cur.key){
cur.left = removeNodeRecursive(cur.left,key);
}else if(key > cur.key){
cur.right = removeNodeRecursive(cur.right, key);
}else{
if(cur.left == null){
return cur.right;
}else if(cur.right == null){
return cur.left;
}else{
// 자식 노드 두개인 경우
Node predecessor = cur;
Node successor = cur.left;
while(successor.right != null){
predecessor = successor;
successor = successor.right;
}
predecessor.right = successor.left;
cur.key = successor.key;
}
}
return cur;
}
public void levelOrder(Node node){
Queue<Node> queue = new LinkedList<>();
queue.add(node);
while(!queue.isEmpty()){
Node cur = queue.poll();
System.out.print(cur.key + " ");
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
}
System.out.println();
}
}
public class Practice1 {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree(20);
bst.head = bst.addNodeRecursive(bst.head, 10);
bst.head = bst.addNodeRecursive(bst.head, 30);
bst.head = bst.addNodeRecursive(bst.head, 1);
bst.head = bst.addNodeRecursive(bst.head, 15);
bst.head = bst.addNodeRecursive(bst.head, 25);
bst.head = bst.addNodeRecursive(bst.head, 13);
bst.head = bst.addNodeRecursive(bst.head, 35);
bst.head = bst.addNodeRecursive(bst.head, 27);
bst.head = bst.addNodeRecursive(bst.head, 40);
bst.levelOrder(bst.head);
bst.head = bst.removeNodeRecursive(bst.head, 40);
bst.levelOrder(bst.head);
bst.head = bst.removeNodeRecursive(bst.head, 25);
bst.levelOrder(bst.head);
bst.head = bst.removeNodeRecursive(bst.head, 20);
bst.levelOrder(bst.head);
}
}