기초 수학 정리(점화식,재귀함수,지수와 로그, 알고리즘 복잡도)

점화식(Recurrence)

어떤 수열의 일반항을 그 이전의 항들을 이용해서 정의하는 식

ex) 피보나치 수열
1,1,2,3,5,8,13 ....

재귀함수

어떤 함수가 자신을 다시 호출하여 작업을 수행하는 방식

반환타입 함수이름(매개 변수){
	종료 조건
    ...
    
    함수 이름(...)
}

public class Main {

    static int recursion1(int n){
        // 1번 문제 해결을 위한 메서드
        if(n==1) return 1;
        return 3 * recursion1(n-1);
    }

    static int recursion2(int n){
        if(n==1) return 1;
        return n + recursion2(n-1);
    }

    static int recursion3(int n){
        // 이러한 메서드는 같은 계산을 계속해서 진행함
        if(n < 3) return 1;
        return recursion3(n-2) + recursion3(n-1);
    }

    public static void main(String[] args) {

        // 점화식 -> 반복문, 재귀 함수

        // 1번 문제 1,3,9,27,... 의 n번째 수

        int n = 4; int result = 1;
        for(int i = 0; i < n; i++){
            if(i==0){
                result = 1;
            }else{
                result *= 3;
            }
        }
        System.out.println(result);

        // 2번 문제 1,2,3,4,5,6, ... 의 n번째 까지의 합
        n = 5; result = 0;
        for(int i = 1; i <= n; i++){
            result += i;
        }
        System.out.println(result);

        // 3번 문제 피보나치 수열 1,1,2,3,5,8,13, ..의 n번째 수
        n = 6;
        result = 0;
        int a1 = 1;
        int a2 = 1;

        if (n < 3) result = 1;
        else{
            for(int i = 2; i < n; i++){
                result = a1 + a2;
                a1 = a2;
                a2 = result;
            }
        }
        System.out.println(result);

    }
}

최대 공약수를 재귀함수로 구현한 예시

static int gcd(int a, int b) {
        if(a % b == 0){
            return b;
        }
    return gcd(b, a%b);
}

---

지수와 로그

제곱근 : a를 제곱하여 b가 될때 a를 b의 제곱근이라고 함

로그 : a가 b가 되기 위해 제곱해야 하는 수

public class Main {

    public static void main(String[] args) {
        // 제곱, 제곱근, 지수

        // 제곱
        System.out.println(Math.pow(2,3));
        System.out.println(Math.pow(2,-3));

        //제곱근
        System.out.println(Math.sqrt(16));
        System.out.println(Math.pow(16, 1.0/2));
        System.out.println(Math.pow(16, 1.0/4));

        // 로그
        System.out.println(Math.E); // 2.71828~~~
        System.out.println(Math.log(2.718281828459045)); // 밑이 10인 상용로그가 아닌 자연로그
        System.out.println(Math.log10(1000));
    }
}

제곱 및 제곱근 메서드 구현

	static double pow(int a, double b){
        double result = 1;
        boolean isMinus = false;

        if(b == 0) return 1;
        else if(b < 0){
            b *= -1;
            isMinus = true;
        }

        for(int i = 0; i < b; i++){
            result *= a;
        }

        return isMinus ? 1 / result : result;
    }

    static double sqrt(int a){
        double result = 1;

        // 바빌로니아 방법
        for(int i = 0; i < 10; i++){
            result = (result + (a/result)) / 2;
        }
        return result;
    }

---

알고리즘 복잡도

복잡도 : 알고리즘의 성능을 나타내는 척도

• 시간복잡도(Time Complexity) : 알고리즘의 필요 연산 횟수
• 공간복잡도(Space Complexity) : 알고리즘의 필요 메모리

시간복잡도와 공간 복잡도는 Trade-Off 관계

시간 복잡도

어떤 문제를 해결하기 위한 알고리즘의 필요 연산 횟수
-> 보통 Big-O 표기법을 통해 나타냄

• Big-O : 알고리즘의 최악의 경우 몇번의 연산을 거친다를 나타냄
• Big-Omega : 알고리즘 실행 시간의 최솟값을 나타냄
• Big-Theta : 알고리즘의 평균 실행 시간을 나타냄
• Little-O : 알고리즘의 실행 시간의 상한보다 더 빠르게 증가하는 함수 나타냄
  -> 알고리즘의 실행 시간이 매우 빨리 증가하는 경우 사용
• 평균 시간 복잡도 : 입력값에 대한 평균적인 실행 시간
  -> Big-O 표기법과 다르게 입력값이 여러 경우에 따라 변할 수 있기에, 실제로 알고리즘의 실행 시간을 예측하는데 더 정확한 정보 제공

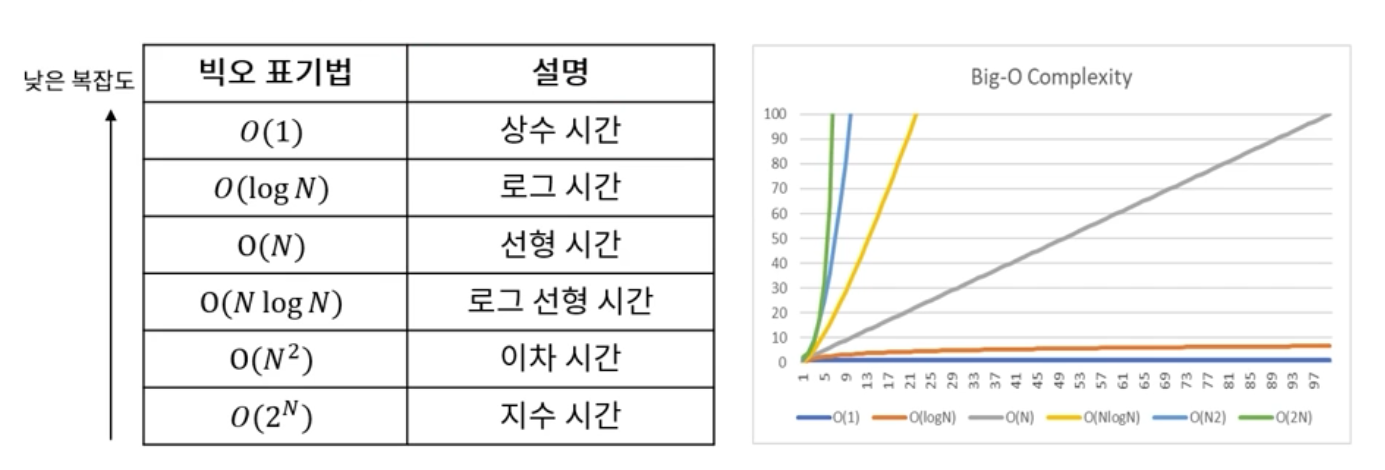
공간 복잡도

어떤 문제를 해결하기 위한 알고리즘의 필요 메모리 사용량
-> 빅오 표기법을 통해 나타냄(일반적으로 메모리 사용량 기준은 MB 단위)

int[] a = new int[1000] ; // 4KB
int[][] a = new int [1000][1000] // 4MB

복잡도 예시 코드

// O(1)
System.out.println("hello");

// O(logN)
for(int i = 1; i < 16; i*=2){
	System.out.println("hello")
}

// O(N)
for(int i = 1; i < 16; i++){
	System.out.println("hello");
}

// O(NlogN)
for(int i = 0; i < 2; i++){
	for(int j = 1; j < 8; j*=2){
    	System.out.println("hello");
    }
}

// O(N^2)
for(int i = 0; i < 2; i++){
	for(int j = 1; j < 8; j*++){
    	System.out.println("hello");
    }
}

// O(2^N)
System.out.println(fibonacci(6));

// 공간복잡도 (O(N))
int n = 3; System.out.println(factorial(n));

// 공간복잡도 (O(1))
int result = 1;
for(int i = 1; i <= n; i++){
	result *= i;
}

---