백트래킹 개념 및 연습 문제

백트래킹

모든 경우의 수를 탐색하며 최적해를 구하는 과정에서 유망하지 않은 쪽은 더 이상 구하지 않는 방법
-> 돌 다리도 두드려 보고 가는 느낌!

Promising : 해가 될 가능성이 있는 경우 유망하다고 함
Pruning(가지치기) : 해가 될 가능성이 없는 경우 해당 노드를 제외 하는 것
BackTracking : 유망하지 않은 쪽으로 가지 않고 되돌아 오는 것

기본적으로 재귀함수 및 DFS를 자유자재로 구현할 줄 알아야 함!

N-Queen 문제

N x N 체스판에서 퀸 N개를 서로 공격할 수 없도록 배치하는 경우의 수

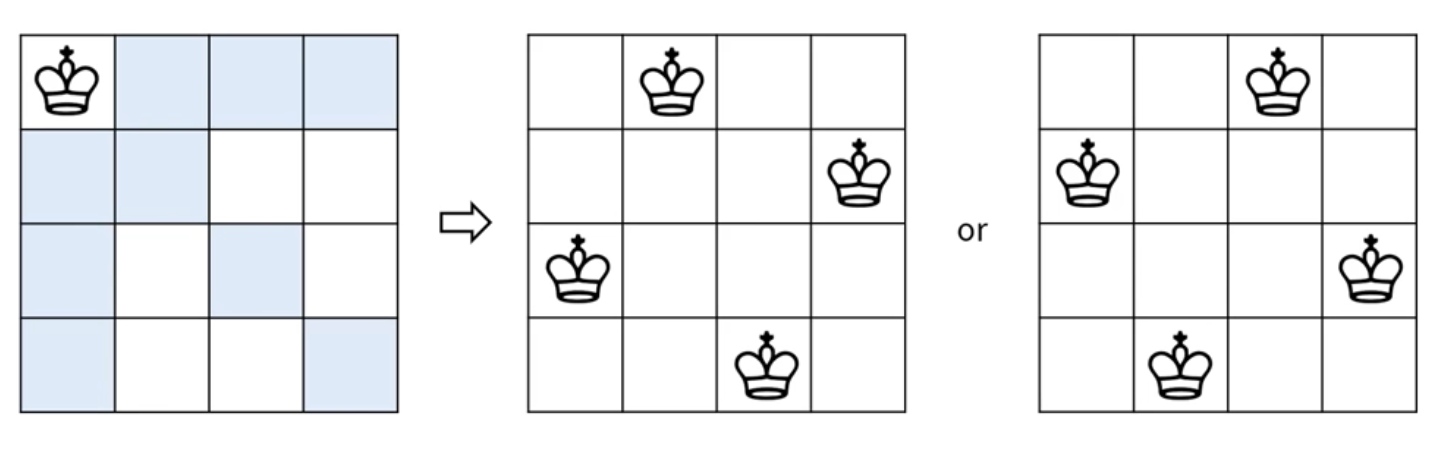
위 경우 퀸을 4 x 4에서 4개 배치

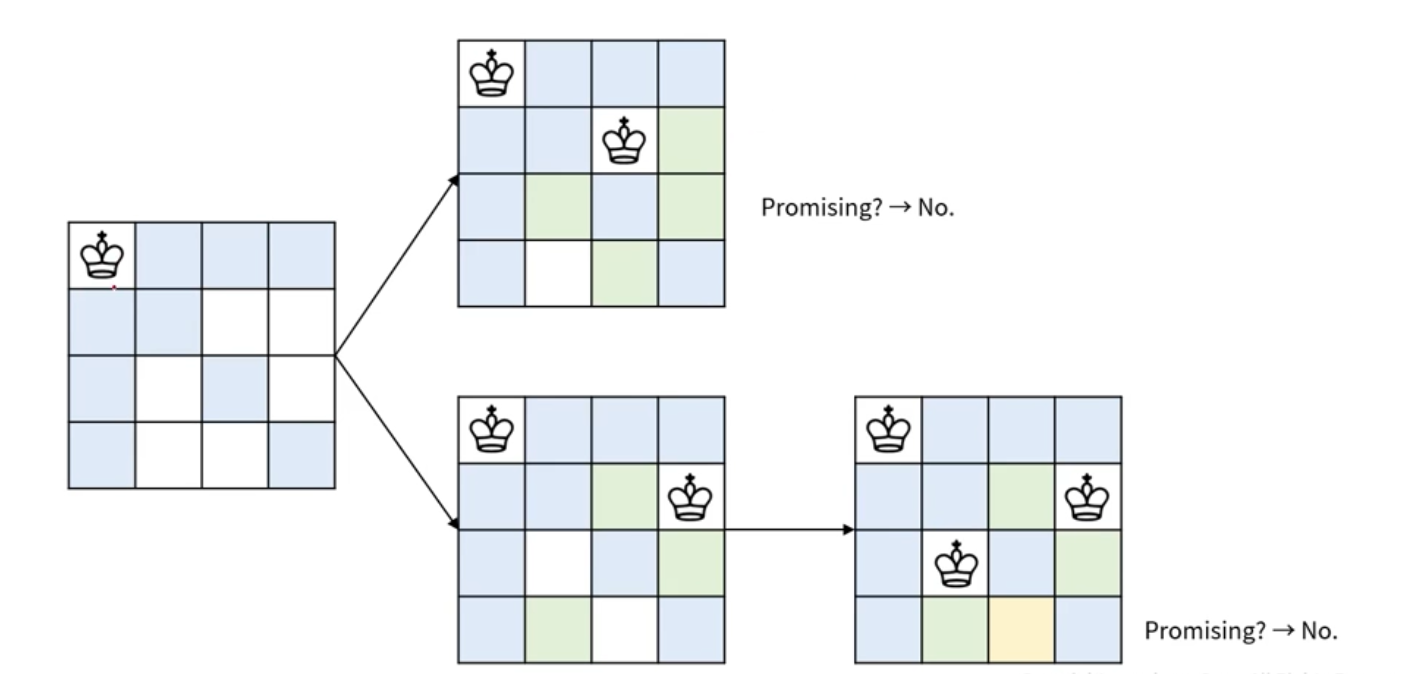
처음에 퀸을 둔 후 다음 퀸을 배치(이동 방향에 걸리지 않는 곳에)할 때

이후 두번째 퀸을 배치함으로써 두면 안되는 곳을 초록색으로(가지치기) .....
-> 위와 같은 로직 반복

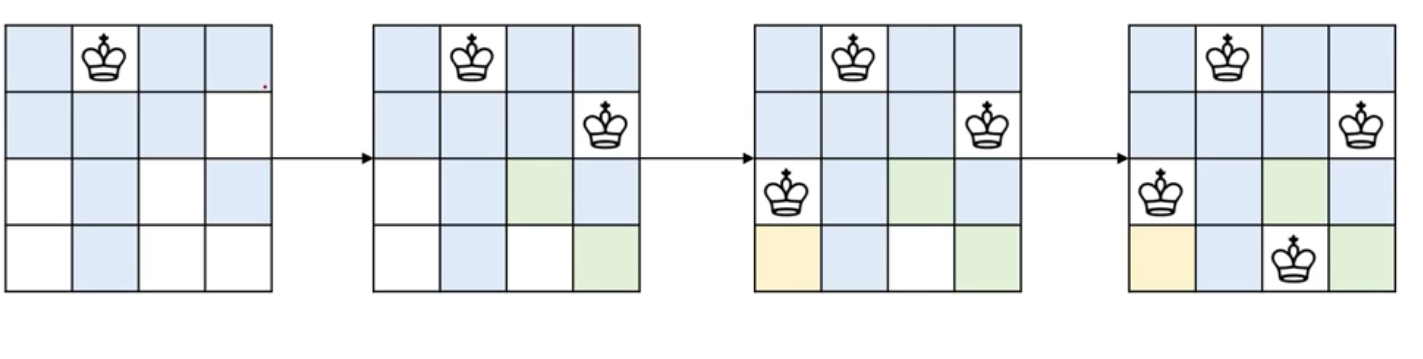
구현 예시

// 알고리즘 - 백트래킹

public class Main {

    static int n = 4;
    static int[] board = new int[n]; // 이 행에 몇번째의 퀸을 두었는지 기록할 배열
    static int cnt;

    public static int nQueen(int row) {
        if(row == n ){
            // 모든 퀸을 놓은 경우
            cnt++;
            for (int i = 0; i < n; i++) {
                System.out.print(board[i] + " ");
            }
            System.out.println();
            return cnt;
        }

        for (int i = 0; i < n; i++) {
            board[row] = i;

            // promising
            if(isPromising(row)){
                nQueen(row + 1);
            }
        }

        return cnt;
    }

    public static boolean isPromising(int row){
        for(int i = 0; i < row; i++){
            if(board[row] == board[i] || row - i == Math.abs(board[row] - board[i])){
                return false;
            }
        }
        return true;
    }

    public static void main(String[] args) {
        // Test code
        Arrays.fill(board,-1); // 혹시나 해서 내가 추가함
        System.out.println("경우의 수: " + nQueen(0));  // 2
    }
}

연습 문제

문제 1

// Practice1
// 정수형 n과 m이 주어졌을 때,
// 1 부터 n 까지의 정수 중에서 중복 없이 m 개를 고른 수열을 출력하는 프로그램을 작성하세요.

// 입출력 예시
// n: 3
// m: 2
// 출력: [1, 2], [1, 3], [2, 1], [2, 3], [3, 1], [3, 2]
// Permutation 문제

import java.util.Arrays;

public class Practice1 {

    public static boolean[] visited;
    public static int[] out;

    public static void solution(int n, int m) {
        visited = new boolean[n];
        out = new int[m];
        permutation(n,m,0);
    }

    public static void permutation(int n, int m, int depth){
        if(depth == m){
            System.out.println(Arrays.toString(out));
            return;
        }

        for (int i = 0; i < n; i++) {
            if(!visited[i]){
                visited[i] = true; // 가지치기
                out[depth] = i + 1;
                permutation(n,m,depth+1);
                visited[i] = false;
            }
        }
    }

    public static void main(String[] args) {
        // Test code
        solution(3, 2);
        System.out.println();
        solution(4, 3);
    }
}

문제 2

// Practice2
// 숫자 7193 은 7193 도 소수이고,
// 719, 71, 7 도 각각 소수이다.
// n 이 주어졌을 때, n 자리 수 중에 위와 같은 소수를 찾는 프로그램을 작성하세요.

// 입출력 예시
// 입력 n: 3
// 출력: 233, 239, 293, 311, 313, 317, 373, 379, 593, 599, 719, 733, 739, 797


import java.util.ArrayList;

public class Practice2 {
    public static ArrayList<Integer> result;

    public static ArrayList<Integer> solution(int n) {
        result = new ArrayList<>();

        // 첫째자리에 올수 있는 숫자 2___, 3____, 5___, 7____
        // 이후 뒤의 숫자에는 0,2,4,6,8,5 중 하나라도 오면 백트래킹 시킴

        int[] primeNum = {2,3,5,7};
        for (int i = 0; i < primeNum.length; i++) {
            // backTracking()
            backTracking(primeNum[i], 1, n);
        }
        return result;
    }

    public static void backTracking(int prime, int len, int n){
        if(len >= n){
            result.add(prime);
            return;
        }

        for (int i = 0; i < 10; i++) {
            if(i % 2 != 0 || i != 5){
                int primeCandidate = prime * 10 + i;
                if(isPrimeNumber(primeCandidate)){
                    backTracking(primeCandidate, len + 1, n);
                }
            }
        }
    }

    public static boolean isPrimeNumber(int num){
        for(int i = 2; i <= num/2; i++){
            if(num % i == 0){
                return false;
            }
        }
        return true;
    }

    public static void main(String[] args) {
        // Test code
        System.out.println(solution(3));
        System.out.println();
        System.out.println(solution(4));
    }
}

문제 3

// Practice3
// sols 배열에 5지 선다 문제의 정답들이 적혀있다.
// 3번 연속 해서 같은 정답이 있는 경우가 없다는 것을 알아낸 후,
// 문제를 찍어서 푼다고 할 때, 5점 이상을 받을 경우의 수를 출력하세요.

// 문제는 총 10문제이며 각 문제당 1점이다.

// 입출력 예시
// sols: {1, 2, 3, 4, 5, 1, 2, 3, 4, 5}
// 결과: 261622


public class Practice3 {
    final static int numOfProblems = 10;
    static int cnt;

    public static void solution(int[] sols) {
        if (sols == null || sols.length != numOfProblems) {
            return;
        }

        cnt = 0;
        int[] submit = new int[numOfProblems]; // 내가 푼 값들

        // backTracking
        backTracking(sols,submit, 0, 0);
        System.out.println(cnt);
    }

    public static void backTracking(int[] sols, int[] submit, int correctCnt, int idx){
        if(numOfProblems - idx + correctCnt < 5){
            return;
        }

        if(idx == numOfProblems){
            // 10번 까지 푼 경우
            if(correctCnt >= 5){
                cnt += 1;
            }
        }else{
            int twoInRow = 0; // 3연속 정답인 케이스 없음
            if(idx >= 2){
                if(submit[idx-1] == submit[idx - 2]){
                   twoInRow = submit[idx - 1];
                }
            }

            for (int i = 1; i <= 5 ; i++) {
                if(i == twoInRow){
                    continue;
                }

                submit[idx] = i;
                if(sols[idx] == i){
                    backTracking(sols, submit, correctCnt + 1, idx + 1);
                }else{
                    backTracking(sols, submit, correctCnt, idx+1);
                }
                submit[idx] = 0;
            }
        }


    }

    public static void main(String[] args) {
        // Test code
        int[] sols = {1, 2, 3, 4, 5, 1, 2, 3, 4, 5};
        solution(sols);

        sols = new int[] {1, 1, 2, 2, 3, 3, 4, 4, 5, 5};
        solution(sols);
    }
}

문제 4

// Practice4
// 2차원 배열 board 가 주어졌다.
// 해당 배열 데이터에는 'o', '#', '.' 의 정보가 기입되어 있다.
// 'o': 동전을 의미
// '#': 벽을 의미
// '.': 빈칸을 의미

// 동전은 항상 두개가 주어진다.
// 두 동전이 함께 이동하다가 하나가 보드에서 떨어지는 경우의 최소 이동 횟수를 출력하는 프로그램을 작성하세요.
// 단, 이동 규칙은 다음과 같다.
// 동전은 좌, 우, 위, 아래로 이동 가능하며 같은 방향으로 함께 이동
// 빈칸이나 동전이 있는 칸으로는 이동 가능
// 벽일 때는 이동 불가
// 이동 횟수가 10번을 넘으면 중지하고 -1 반환

// 입출력 예시
// board: {{'.', '#'}, {'.', '#'}, {'.', '#'}, {'o', '#'}, {'o', '#'}, {'#', '#'}}
// 결과: 4


import java.util.ArrayList;

public class Practice4 {
    final static int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    static int cnt;

    static class Coin {
        int x;
        int y;

        public Coin(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

    public static void solution(char[][] board) {
        if (board == null || board.length == 0 || board[0].length == 0) {
            return;
        }

        int n = board.length;
        int m = board[0].length;
        cnt = Integer.MAX_VALUE;

        ArrayList<Coin> coins = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                // 동전 2개 찾아서 coins 에 추가
                if (board[i][j] == 'o') {
                    coins.add(new Coin(j, i));
                }
            }
        }

        Coin coin1 = coins.get(0);
        Coin coin2 = coins.get(1);
        backTracking(board, m, n, coin1.x, coin1.y, coin2.x, coin2.y, 0);
        System.out.println(cnt == Integer.MAX_VALUE ? -1 : cnt);
    }

    public static void backTracking(char[][] board, int m, int n, int x1, int y1, int x2, int y2, int moveCnt) {
        // 10번 이상 이동하는 경우 return
        if (moveCnt >= 10) {
            return;
        }

        // 두 동전은 같은 방향으로 함께 이동
        for (int[] dir: dirs) {
            // 1번 동전 다음 위치
            int x1Next = x1 + dir[0];
            int y1Next = y1 + dir[1];

            // 2번 동전 다음 위치
            int x2Next = x2 + dir[0];
            int y2Next = y2 + dir[1];

            // 밖으로 떨어진 동전 개수 세는 용
            int dropCnt = 0;

            // 떨어졌는지 확인
            if (x1Next < 0 || x1Next >= m || y1Next < 0 || y1Next >= n) {
                dropCnt += 1;
            }

            if (x2Next < 0 || x2Next >= m || y2Next < 0 || y2Next >= n) {
                dropCnt += 1;
            }

            // 두 동전 중 하나만 떨어뜨려야 하므로 이 경로는 continue 처리
            if (dropCnt == 2) {
                continue;
            }

            // 하나 떨어졌으면 cnt 반환
            if (dropCnt == 1) {
                cnt = Math.min(cnt, moveCnt + 1);
                return;
            }

            // 벽이면 제자리로 두고 다음 진행
            if (board[y1Next][x1Next] == '#') {
                x1Next = x1;
                y1Next = y1;
            }

            // 벽이면 제자리로 두고 다음 진행
            if (board[y2Next][x2Next] == '#') {
                x2Next = x2;
                y2Next = y2;
            }

            backTracking(board, m, n, x1Next, y1Next, x2Next, y2Next, moveCnt + 1);
        }
    }

    public static void main(String[] args) {
        // Test code
        char[][] board = {{'.', '#'}, {'.', '#'}, {'.', '#'}, {'o', '#'}, {'o', '#'}, {'#', '#'}};
        solution(board);

        board = new char[][] {{'#', '#', '#'}, {'.', 'o', '.'}, {'#', '.', '#'}, {'.', 'o', '.'}, {'#', '#', '#'}};
        solution(board);

        board = new char[][] {{'#', '#', '#'}, {'.', 'o', '.'}, {'#', '#', '#'}, {'.', 'o', '.'}, {'#', '#', '#'}};
        solution(board);
    }
}