다이나믹 프로그래밍(DP) 개념 및 연습 문제

다이나믹 프로그래밍

큰 문제를 부분 문제로 나눈 후 답을 찾아가는 과정에서(Divide and conquer),계산된 결과를 기록하고 재활용하며 문제의 답을 구하는 방식
-> 중간 계산 결과를 기록하기 위한 메모리가 필요
-> 한번 계산한 부분을 다시 계산하지 않아 속도가 빠름

분할 정복과의 차이

• 분할 정복은 부분 문제가 중복되지 않음(ex: 합병 정렬과 같은 문제, 각각 독립되어 처리)
• DP는 부분 문제가 중복되어 재활용에 사용

그리디와의 차이
-> 그리디는 순간의 최선을 구하는 방식(근사치), 반면 DP는 모든 방법을 확인 후 최적해를 구하는 방식

예시

피보나치

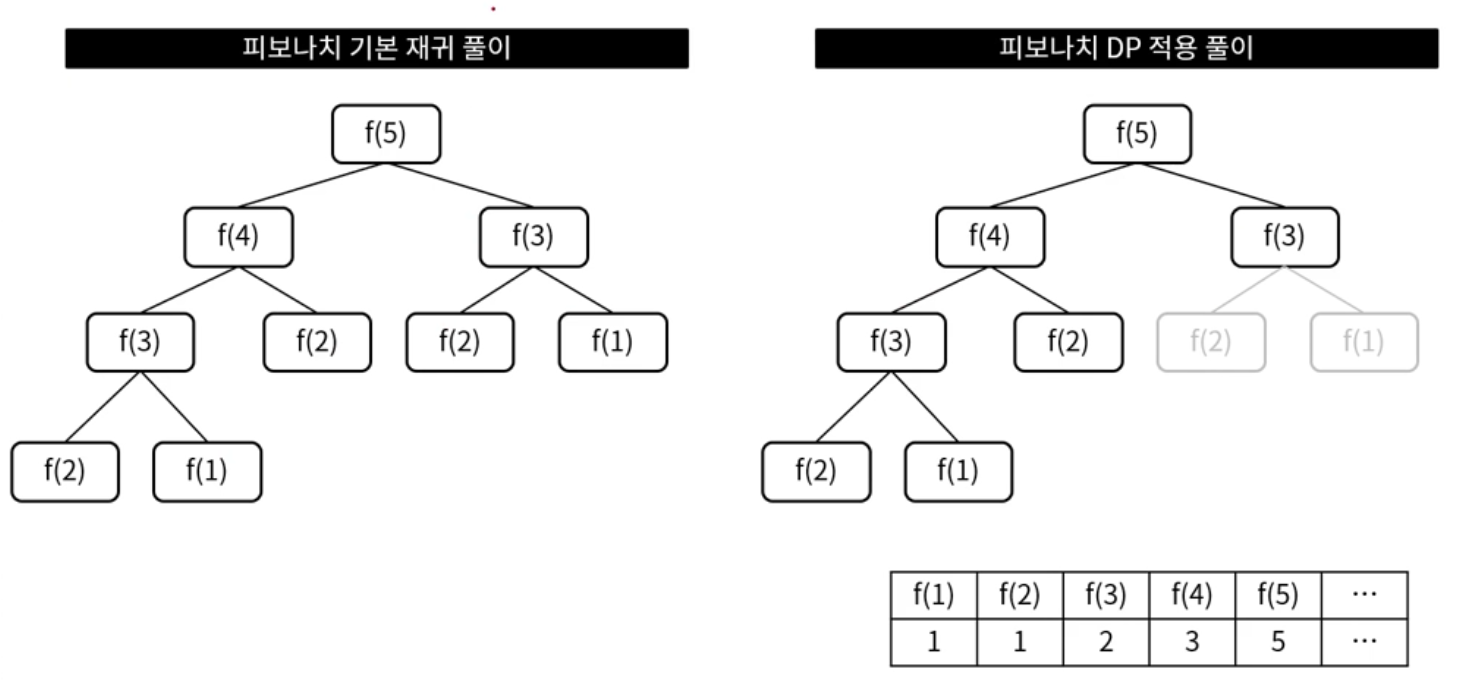
DP용 메모리에 먼저 계산된 값을 기록해 둠(Bottom Up)

구현 방법

1. 타뷸레이션(Tabulation)
   상향식 접근 방법(bottom up)
   작은 하위 문제부터 풀면서 올라감, 모두 계산하면서 차례대로 진행

2. 메모이제이션(Memoization)
   하향식 접근 방법(top down)
   큰 문제에서 하위 문제를 확인해가며 진행, 계산이 필요한 순간 계산하며 진행

// 알고리즘 - 다이나믹 프로그래밍

public class Main {
    // 피보나치 수열(일반 풀이 - O(n^2)) : 계산했던 부분도 다시 계산
    public static int fib(int n) {
        if(n <= 1){
            return n;
        }else{
            return fib(n-1) + fib(n-2);
        }
    }

    // 피보나치 수열(DP - Tabulation - O(n))
    public static int fibDP(int n) {
        int[] dp = new int[n < 2? 2: n+1];
        dp[0] = 0; dp[1] = 1;

        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i-1] + dp[i-2];
        }

        return dp[n];
    }

    // 피보나치 수열(DP - Memoization - O(n))
    static int[] dp = new int[8];
    public static int fibDP2(int n) {
        if(n <= 2){
            return 1;
        }
        if(dp[n] != 0){
            return dp[n];
        }

        dp[n] = fibDP2(n-1) + fibDP2(n-2);
        return dp[n];
    }

    public static void main(String[] args) {
        // Test code
        System.out.println(fib(7));
        System.out.println(fibDP(7));
        System.out.println(fibDP2(7));
    }
}

연습문제

문제 1

// Practice
// 정수 n 이 주어졌을 때 아래의 연산을 통해 1로 만들려고 한다.
    // 2로 나누어 떨어지면 2로 나누기
    // 3으로 나누어 떨어지면 3으로 나누기
    // 1 빼기
// 위의 연산을 통해 1로 만들 때 필요한 최소한의 연산 횟수를 출력하는 프로그램을 작성하세요.

// 입출력 예시
// n: 2
// 출력: 1

// n: 9
// 출력: 2

public class Practice1 {
    public static int solution(int n) {
        int[] dp = new int[n+1];

        for(int i = 2; i <= n; i++){
            dp[i] = dp[i-1] + 1; // 디폴트로 우선 넣어둠

            if(i % 2 == 0){
                dp[i] = Math.min(dp[i], dp[i / 2] + 1);
            }

            if(i % 3 == 0){
                dp[i] = Math.min(dp[i], dp[i/3] + 1);
            }
        }

        return dp[n];
    }

    public static void main(String[] args) {
        // Test code
        System.out.println(solution(2));    // 1
        System.out.println(solution(4));    // 2
        System.out.println(solution(9));    // 2
        System.out.println(solution(10));   // 3
    }
}

문제 2

// Practice
// 수열 arr 이 주어졌을 때,
// 부분 수열 중 증가하는 부분이 가장 긴 길이를 출력하는 프로그램을 작성하세요.

// 입출력 예시
// arr: {10, 20, 30, 10, 50, 10}
// 출력: 4

public class Practice2 {
    public static int solution(int[] arr) {
        int n = arr.length;
        int[] dp = new int[n+1];

        int result = 0;
        for (int i = 1; i <= n; i++) {
            dp[i] = 1;
            for (int j = 1; j < i; j++) {
                if(arr[j-1] < arr[i - 1]){
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            result = Math.max(result,dp[i]);
        }

        return result;
    }

    public static void main(String[] args) {
        // Test code
        int[] arr = new int[]{10, 20, 30, 10, 50, 10};
        System.out.println(solution(arr));
    }
}

문제 3

// Practice
// 배낭에 물품을 담으려고 한다.
// 배낭에는 k 무게 만큼의 물품을 담을 수 있다.
// n 개의 물품이 주어지고 이 물품의 무게와 가치 정보가 items 2차원 배열에 주어졌을 때,
// 최대 가치가 되도록 물품을 담았을 때의 가치를 출력하는 프로그램을 작성하세요.

// 입출력 예시
// items: {{6, 13}, {4, 8}, {3, 6}, {5, 12}}
// n: 4
// k: 7
// 출력: 14

// 부분 문제나 겹치는 부분이 있는지 확인해보자
public class Practice3 {

    public static int solution(int[][] items, int n, int k) {
        int[][] dp = new int[n + 1][k + 1];

        for (int i = 0; i < n; i++) {
            for (int j = 1; j <= k; j++) {
                if(items[i][0] > j){
                    dp[i + 1][j] = dp[i][j]; // 현재 넣을려고 하는 물건이 j보다 큰 경우 , 이전 값이 그대로 내려옴
                }else{
                    dp[i + 1][j] = Math.max(dp[i][j], dp[i][j - items[i][0]] + items[i][1]);
                }
            }
        }

        return dp[n][k];
    }

    public static void main(String[] args) {
        // Test code
        int[][] items = {{6, 13}, {4, 8}, {3, 6}, {5, 12}};
        System.out.println(solution(items, 4, 7));  // 14
    }
}