Algorithm_java

기본기부터 다시 쌓는 알고리즘 공부를 시작해보자자바 8, 더자바 강의도 병행하면서 하고있는데 거기서 익히는 기능들도 많이 활용하면서 풀도록 해야겠다모든 코드는 자바로 구현하였다

처음부터 끝까지 길이가 N인 배열에 대해서 순회하면서 가장 큰값을 맨 뒤로 옮겨주는 방식으로두 인접한 원소를 비교하여 순서가 맞지않다면 교환하여 정렬하는 방법O(n^2)자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아

재귀(Recursion)는 자신을 정의할 때 자기 자신을 재참조하는 방법이다재귀함수는 전형적인 스택의 구조로 움직인다메모이제이션 기법을 활용한 팩토리얼 재귀함수각 케이스별로 결과값을 확인해서 규칙이나 점화식을 찾아서 구현해야한다

입력크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서보다 큰 크기의 부분 문제를 해결, 최종적으로 전체 문제를 해결하는 알고리즘Memoization 기법을 사용한다상향식 접근법이다프로그램 실행시 이전에 계산한 값을 지정하며, 다시 계산하지 않도록

문제를 나눌 수 없을때 까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘하양식 접근법이다일반적으로 재귀함수로 구현을 많이한다문제를 잘게 쪼갤때, 부분문제는 중복되지 않는다Memoization기법을 사용하지 않는다ex) 병합 정렬, 퀵 정렬pivot

재귀를 주로 사용리스트를 divide하면서 반복list : 데이터 리스트find_data : 원하는 값진행list의 중간값을 find_data와 비교작으면 맨앞부터 중간값까지 중에서 중간값을 비교크면 중간값부터 맨끝까지 중에서 중간값을 비교이후 계속 반복

탐욕 알고리즘 최적의 해에 가까운 값을 구하기 위해 사용된다 매순간 최적이라고 생각되는 경우를 선택하는 방식 이것이 최종적으로 최적임을 암시하는것은 아니다 예시 동전 문제 지불해야하는 금액이 4720원 일 때, 1, 50, 100, 500원 동전으로 동전수가

그래프는 실제 세계의 현상이나 사물을 정점(Vertex) 또는 노드(Node)와 간선(Edge)로 표현하기 위해 사용노드(Node) : 위치, 정점간선(Edge) : 위치간의 관계를 표시한 선으로 노드를 연결한 선인접 정점(Adjacent Vertex) : 간선으로 직

너비 우선 탐색 : 정점들과 같은 레벨에 있는 노드들을 먼저 탐색하는 방식자료구조 큐를 활용need_visit 큐와 visited 큐처음 두개의 큐는 비어있다need_visit에 첫 노드를 전달해 주면서 시작노드 수 : V간선 수 : E시간 복잡도 : O(V + E)

Depth First Search 깊이 우선 탐색 : 정점의 자식들을 먼저 탐색하는 방식 구현

두 노드를 잇는 가장 짧은 경로를 찾는 문제이다가중치 그래프(Weighted Graph)에서 간선(Edge)의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적단일 출발 및 단일 도착 (single-source and single-destiantion sortes

여기서의 트리구조는 부모 자식형태의 트리구조를 의미하는 것이 아니라싸이클이 발생하지 않는 그래프 구조를 의미한다원래 그래프의 정점 전부와 간선의 부분으로 이루어진 부분 그래프이다따라서 하나의 그래프에 여러개의 스패닝 트리가 나올 수 있다가중치 그래프의 스패닝 트리중 가

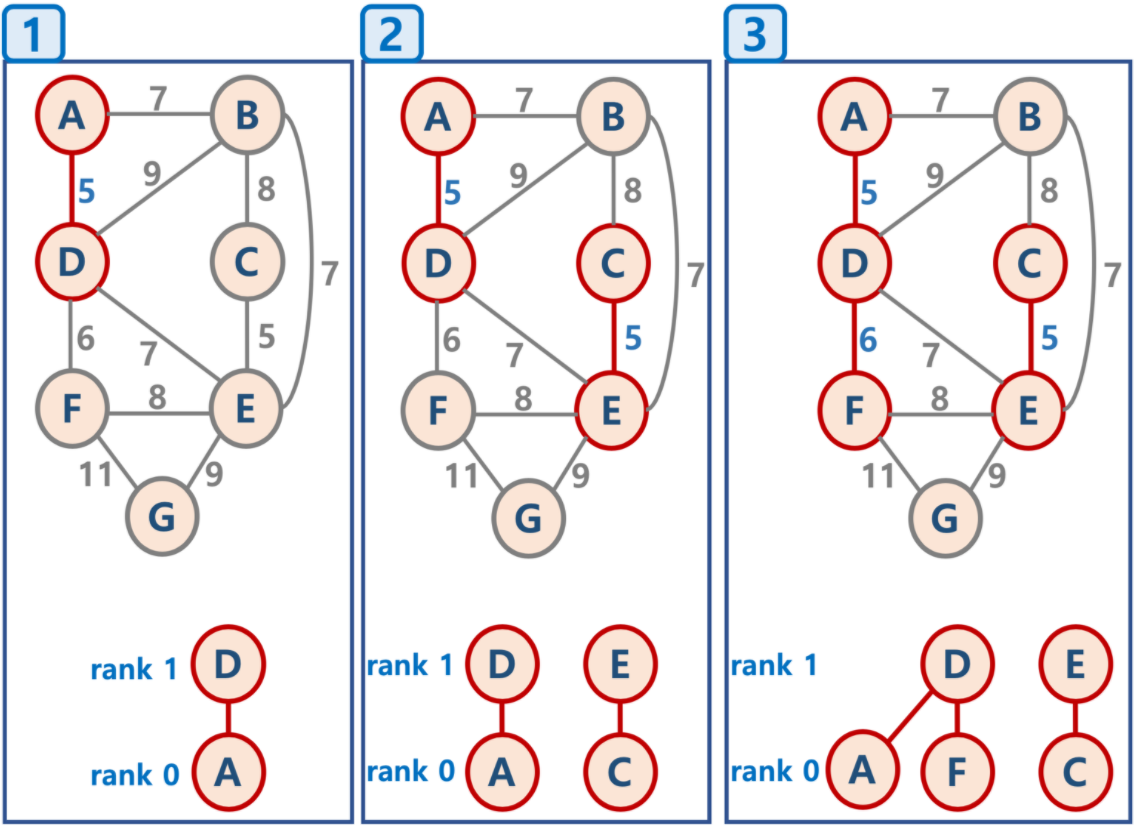
싸이클이 존재하지 않고 모든 노드들이 연결된 최소 가중치 트리를 구해야한다그래프의 모든 간선을 가중치의 오름차순으로 정렬최소 간선부터 스패닝에 하나씩 추가하되 싸아클이 존재하지 않도록 한다모든 정점을 독립적인 집합으로 만든다모든 간선을 비용을 기준으로 정렬하고, 비용이

크루스컬 알고리즘의 시간복잡도는 O(E log E)이다노드의 수 만큼 부분집합을 만드므로 O(V) 소요간선들의 가중치를 기준으로 정렬을 하므로 O(E log E) 소요된다path compression 기법과 union by rank 기법을 이용하여 find, union

백준 - 최소 스패닝 트리 1197번

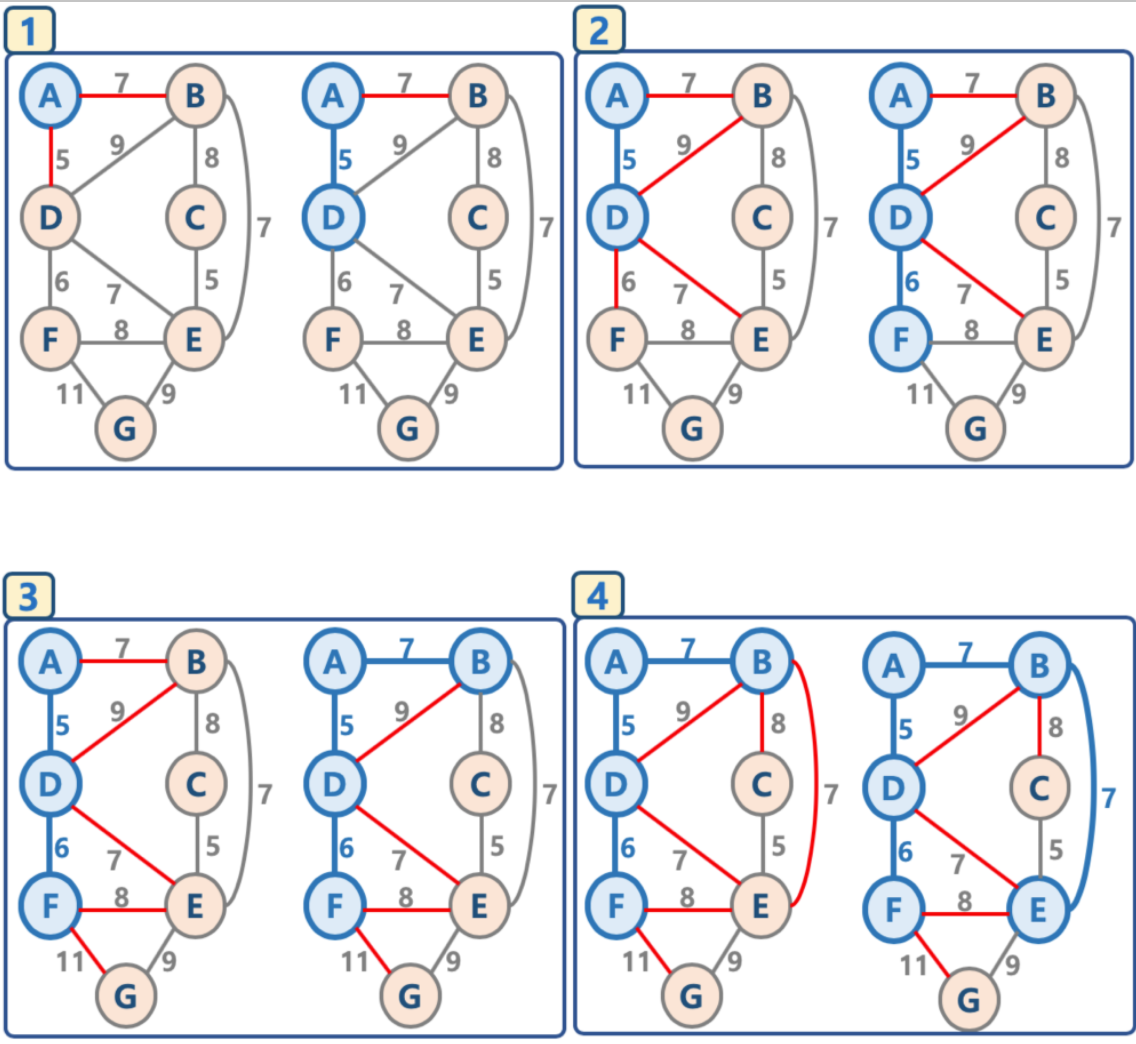
크루스칼 알고리즘가장 작은 가중치부터 큰 가중치까지 순서대로 간선의 연결 상태를 보지 않고 나열 후싸이클 여부만을 확인하면서 추가전체 간선에 대해서 최소값부터프림 알고리즘특정 시작 노드에 연결된 간선들을 확인 후 그 중 가장 작은 가중치의 간선에 대해서 싸이클 여부를

모든 간선 정보를 저장 (adjacent_edges)임의의 정점을 선택, '연결된 노드 집합(connected_nodes)'에 삽입선택된 정점에 연결된 간선들을 간선 리스트(candidate_edge_list)에 삽입간선 리스트(candidate_edge_list)에서

간선이 아닌 노드를 중심으로 우선순위 큐를 적용하는 방식이다시간복잡도가 E log E가 아닌 E log V이다 -> 간선이 복잡한 그래프일 경우 크루스칼 또는 이전 프림알고리즘 보다 시간복잡도가 더욱 개선된다초기화 - (정점 : key)구조를 만들어 놓고, 특정(시작)

제약 조건 만족 문제에서 해를 찾기 위한 전략해를 찾기 위해, 후보군에 제약 조건을 점진적으로 체크하다가, 해당 후보군이 제약조건을 만족할 수 없다고 판단되는 즉시 backTrack(다시는 이 후보군을 체크하지 않을것을 표기)하고, 바로 다음 후보군으로 넘어가며, 결국