1. Vector space(=linear space)
- vector space는 다음과 같이 아래 2가지 조건을 만족하는 벡터들의 집합
- scalar 배가 가능함 ( Scalar Multiplication )
- vector간 합 연산이 가능함 ( Vector Addition )
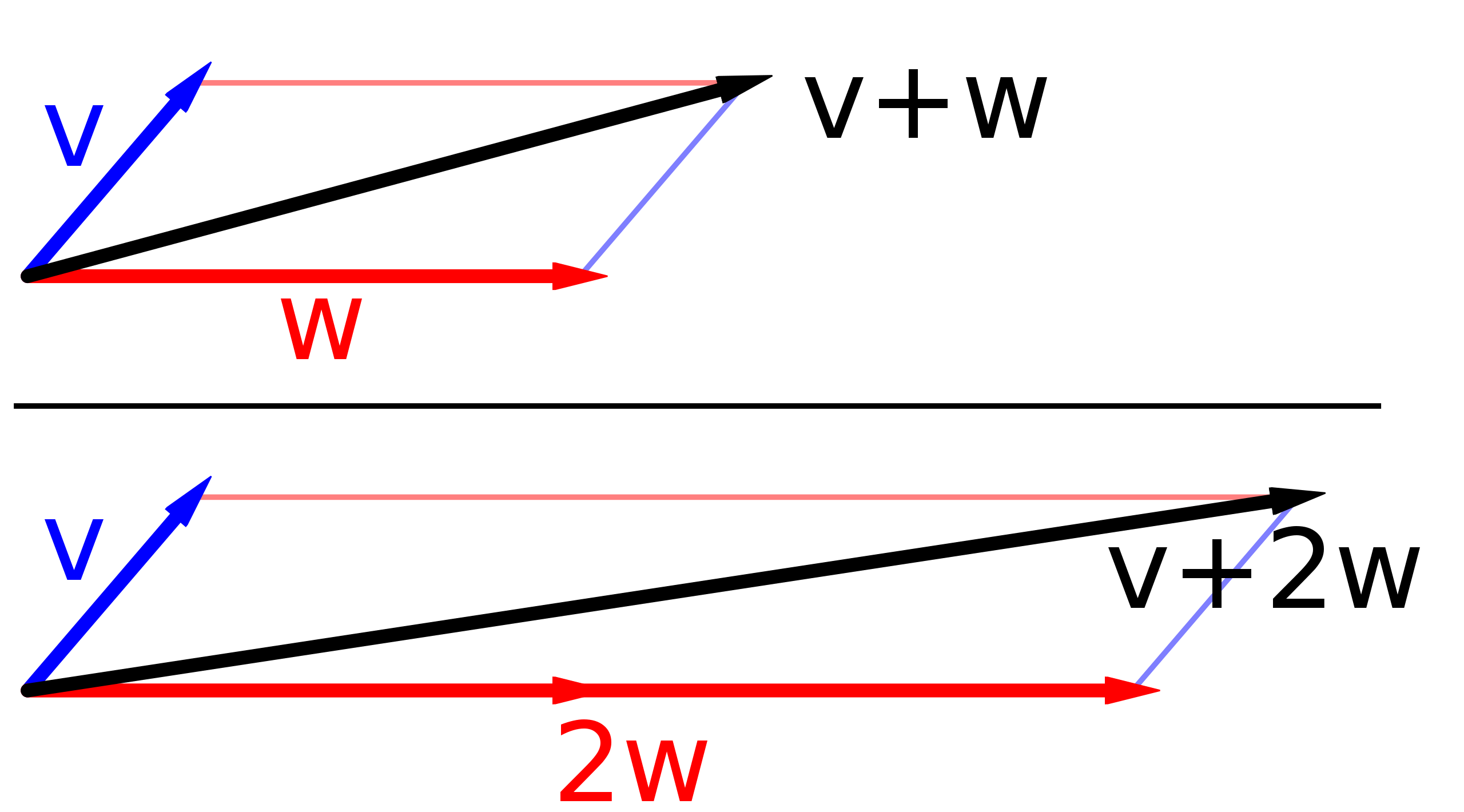
가장 작은 기본 단위인 재료가 되는 벡터를 이용해서 늘리고 더해서 만들 수 있는 공간을 벡터스페이스라고 한다. 우리가 중학교 때 부터 익숙했던
2차원 공간은 x축 방향의 재료벡터와 y축 방향의 재료벡터를 늘리고 더해서 만들었던 공간이다. 재료 벡터란 그렇다면 무엇일까?
2. Linear function(Transformation)
- 2개의 vector space 에 대하여 function 가 아래의 조건을 만족하면 linear function 이라고함.Euclidean spaces간의 모든 linear function은 과 같이 행렬곱으로 표현 가능함
행렬 A와 벡터 x에 대해서 Ax는 x라는 V vector Space에 있는 벡터를 W라는 vector space에 있는 벡터로 변환하는 것이다. 행렬은 함수였다😝
3. Matrix
-
로 가는 linear function으로 볼 수 있음
행렬을 Linear Function으로 볼 수 있음
4. Linear subspace
- 은 아래를 만족하면 의 subspace라고 함
- 만약 이 에 속하고, 에 포함되는 vector들의 선형 결합이 다시 space 에 속하는 경우 이를 subspace라고 함
5. Span
- 만약 이 벡터들에 대해서 Span 되었다는 의미
이번 Linear Algebra 포스팅에서, [x1, x2, ...]는 x1, x2,...의 벡터를 늘리고 더해서 만든 vector space로 정의하기로 해보자. L이라는 벡터공간은 x1,x2,...라는 재료벡터를 이용해서 만든 공간이다.
6. Linear independence
- vector들 간 아래의 관계를 만족하면 이를 Linearly independent(선형 독립)이라고 함
- T.F.A.E.(The Following Are Equivalent)
- 가 선형독립이라면
- 어떤 는 다른 vector들의 선형 결합으로 나타내어 질 수 없음
앞서 이야기했던 벡터공간을 이루기 위한 가장 작은 기본 단위인 재료벡터의 개념을 명확하기 위해 Linear Independence라는 개념이 도입되었다. 벡터 집합안에 있는 어떤 벡터를 다른 벡터들을 늘리고 더해서 만들 수 없다면? 이 벡터는 공간에서 가장 기본이 되는 벡터인것이고, 재료 벡터 즉 Basis Vector가 된다.
7. Basis
- 들이 독립이고 이라면 를 basis라고 부름
- 이 때 vector의 수 를 의 dimension(차원)이라고 부름
- 일 경우 아래를 만족하는 는 unique 함
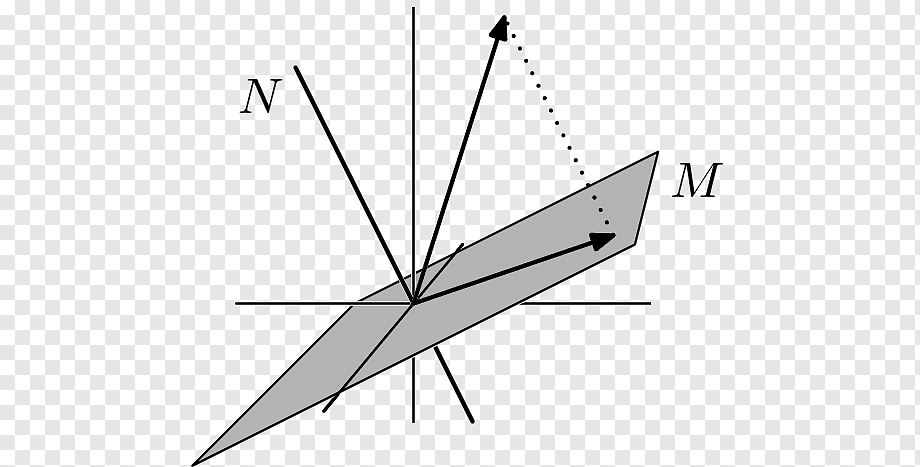

그림 더 그려줘요