유클리드 호제법

정의

• 2개의 자연수 혹은 정식의 최대 공약수를 구하는 알고리즘의 하나.
• 호제법이란 두 수가 서로 상대방 수를 나누어서 결국 원하는 수를 얻는 알고리즘을 나타냄.

1112와 695의 최대공약수

• 최대공약수를 구하기 위해선 소인수분해를 먼저 해야한다.

1112 = 139 X 2 X 2 X 2
695 = 139 X 5

두 수를 소인수 분해 후 공통된 소수를 찾으면 되는데, 이를 통해 139가 정답인 것을 알 수 있지만, 알고리즘에서 이렇게 분해하면 수가 커져 시간 복잡도가 복잡해진다. 그러므로 유클리드 호제법을 사용하면 해결 할 수 있다.

백준 13241번

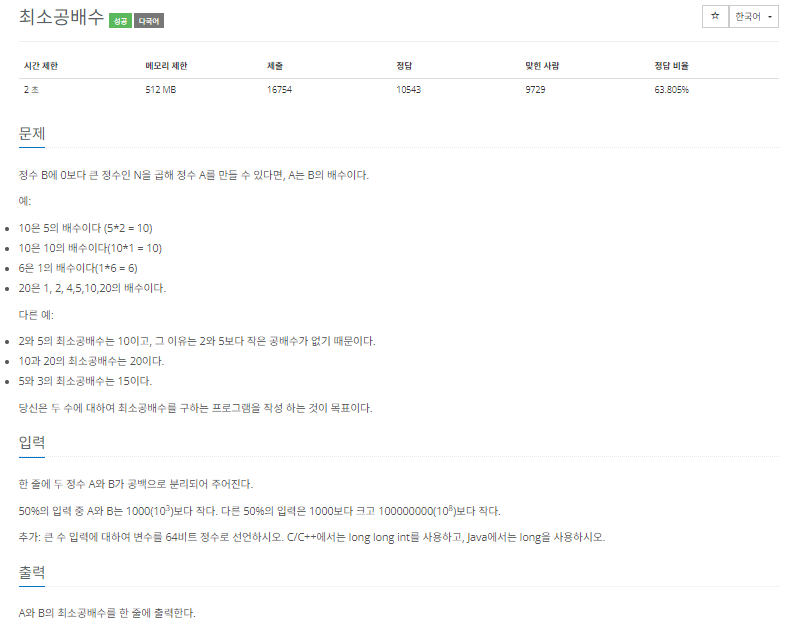
이 문제는 유클리드 호제법을 사용해 최대공약수를 구하는 방식이다. 두 수를 공통된 수로 나눈 후 한 쪽이 0이 나올 때 까지 나눈다면, 나머지 한 쪽이 남아있는 수가 최대공약수가 되는 것이다.

출처 : 링크텍스트

코드

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(bf.readLine());
        long num1 = Integer.parseInt(st.nextToken());
        long num2 = Integer.parseInt(st.nextToken());


        long N = eucd(Math.max(num1, num2), Math.min(num1, num2));

        num1 = num1 / N;
        num2 = num2 / N;

        long M = num1 * num2 * N;

//            System.out.println(N); 최대 공약수
        bw.write(M + "");  // 최소 공배수
        bw.flush();
        bw.close();
        bf.close();
    }

    static public long eucd(long bn, long sn) {
        long r = bn % sn;
        if (r == 0) {
            return sn;
        } else {
            return eucd(sn, r);
        }
    }
}

핵심코드

static public long eucd(long bn, long sn) {
        long r = bn % sn;
        if (r == 0) {
            return sn;
        } else {
            return eucd(sn, r);
        }
    }

핵심 코드는 eucd 함수에 놓여져 있다. bn(큰 값)과 sn(작은 값)으로 두 수를 입력 받고 작은 값으로 큰 값을 나눈 값을 r에 치환한다. 이 방식은 0이 될 때 까지 계산하며 제일 작은 나머지 값이 나올 때 까지 계산을 이어가면 그 값이 정답이 되는 방식이다.