백트래킹 - 백준 10597 (22.6.14)

백트래킹이란

백트래킹(backtracking)이란 해를 찾는 도중 해가 아니어서 막히면, 되돌아가서 다시 해를 찾아가는 기법을 말한다.

해를 찾아가는 도중, 지금의 경로가 해가 될 것 같지 않으면 그 경로를 더이상 가지 않고 되돌아간다.

즉 답이 될 만한지 판단하고 그렇지 않으면 그 부분까지 탐색하는 것을 하지 않고 가지치기 하는 것을 백트래킹이라고 생각하면 된다.

깊이 우선 탐색(DFS) 과 백트래킹

DFS는 가능한 모든 경로(후보)를 탐색한다. 따라서, 불필요할 것 같은 경로를 사전에 차단하거나 하는 등의 행동이 없으므로 경우의 수를 줄이지 못한다.

따라서, N! 가지의 경우의 수를 가진 문제는 DFS로 처리가 어렵다.

예시 : 백준 10597번 문제

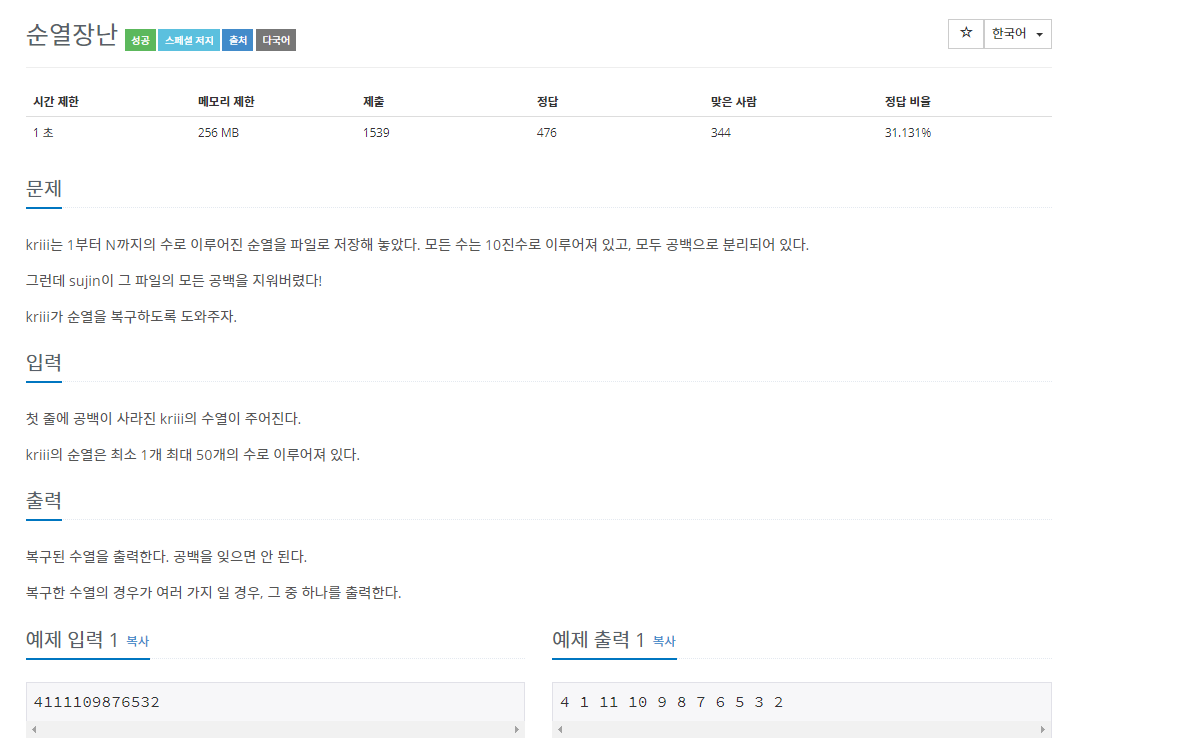
50개의 수를 나타내는 순열의 경우의 수는 50!로 완전 탐색으로는 풀 수 없다. 왼쪽부터 숫자를 하나하나 살펴보며 가능한 순열을 만들어 출력해야한다.

예를 들어 1을 만나면 1을 취할 수도 있고, 1 다음에 나오는 숫자와 합쳐서 두 자리 수를 취할 수도 있다. 만약 이 전에 1을 이미 고른 적이 있다면 두 자리 수를 취할 수 밖에 없다. 그런데 이1이 마지막 숫자라서 다음 숫자가 없다면 순열 만들기에 실패한 것이므로 돌아가서 다른 방법을 찾아야 한다.

이런 전략으로 백트래킹으로 풀 수 있다.

inpu = input()
N = (len(inpu) - 9) // 2 + 9 if len(inpu) > 9 else len(inpu)
check = [False] * (N + 1)
find_ans = False

def bt(i, arr):
    global find_ans
    if i >= len(inpu): # 숫자를 다 썼으면 정답
        find_ans = True
        print(*arr)
        return
    
    n = int(inpu[i])
    if n <= N and not check[n]: # 일단 안쓴숫자면 끼워맞춰보고
        check[n] = True
        narr = arr[:]
        narr.append(n)
        bt(i + 1, narr) # DFS 돌려봐서
        if find_ans: 
            return    
        check[n] = False # 이숫자로 답안나오면 취소하고

    if i + 1 < len(inpu):
        n = int(inpu[i:i+2]) # 두자리 수로 해보기.  결국엔 두가지 경우중 하나다
        if n <= N and not check[n]:
            check[n] = True
            narr = arr[:]
            narr.append(n)
            bt(i + 2, narr)
            if find_ans:
                return
            check[n] = False

bt(0, [])