탐욕 알고리즘(Greedy Algorithm)이란
선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법이다.
최적해를 구하는 데에 사용되는 근사적인 방법이다.
순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다.
탐욕 알고리즘의 조건
탐욕 알고리즘이 잘 작동하는 문제는 대부분 탐욕스런 선택 조건(greedy choice property)과 최적 부분 구조 조건(optimal substructure)이라는 두 가지 조건이 만족된다.
- 탐욕적 선택 속성(Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않는다.
- 최적 부분 구조(Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
이러한 조건이 성립하지 않는 경우에는 탐욕 알고리즘은 최적해를 구하지 못한다.
하지만, 이러한 경우에도 탐욕 알고리즘은 근사 알고리즘으로 사용이 가능할 수 있으며, 대부분의 경우 계산 속도가 빠르기 때문에 실용적으로 사용할 수 있다.
- 근사 알고리즘(approximation algorithm)은 어떤 최적화 문제에 대한 해의 근사값을 구하는 알고리즘을 의미한다.
이 알고리즘은 가장 최적화되는 답을 구할 수는 없지만, 비교적 빠른 시간에 계산이 가능하며 어느 정도 보장된 근사해를 계산할 수 있다.
- 매트로이드 는 탐욕 알고리즘이 언제나 최적해를 찾아낼 수 있는 특별한 구조이다.
매트로이드는 모든 문제에서 나타나는 것은 아니나, 여러 곳에서 발견되기 때문에 탐욕 알고리즘의 활용도를 높여 준다.
백준 1700번 문제
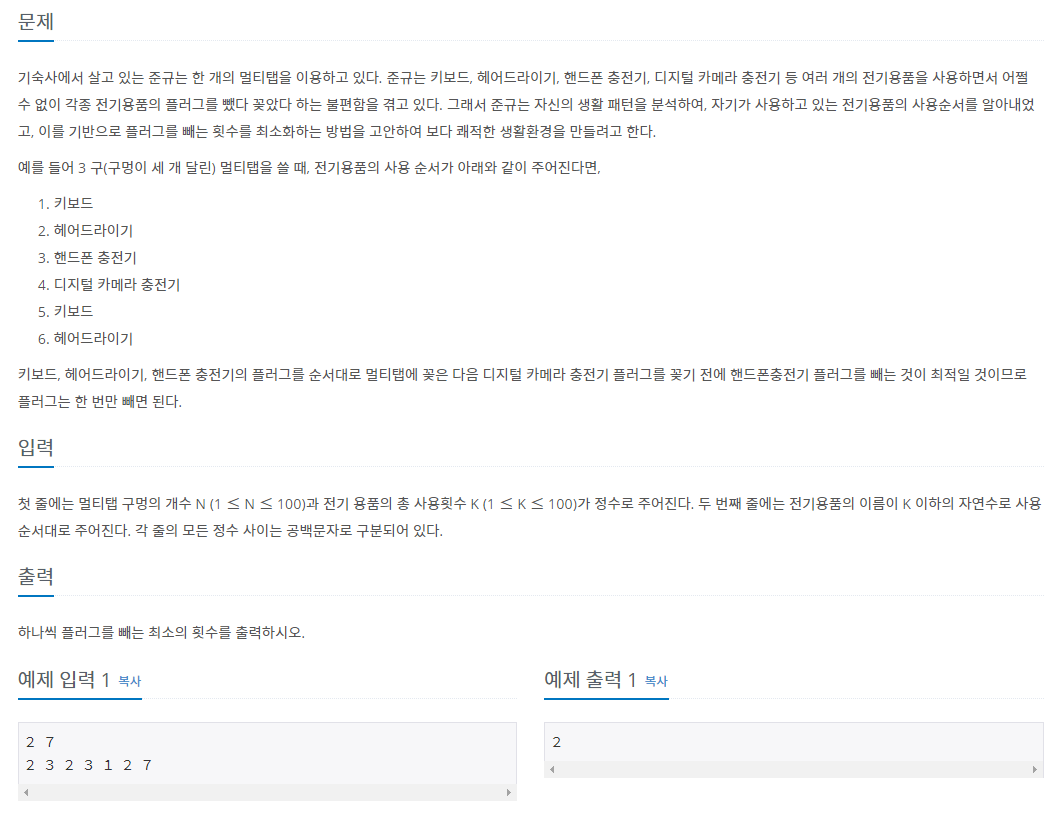
이 문제는 플러그 교체를 하지 않는 시간을 최대한으로 늘리는 그리디 문제이다. 즉, 가장 늦게 사용될 플러그를 빼면 된다.
N, K = map(int, input().split())
arr = list(map(int, input().split()))
multi = []
ans = 0
for i, item in enumerate(arr):
if item in multi: # 꽂혀있는게 사용되면
continue
if len(multi) >= N: # 꽂을곳이 부족하면
last_use = (-1, 0)
for pluged_in in multi: # 멀티탭을 탐색해서
for j in range(i, K):
if pluged_in == arr[j]: # 사용계획을 탐색해서 멀티탭에 꽂혀있는 것 중 가장 늦게 사용되는 것 찾기
last_use = (pluged_in, j) if j > last_use[1] else last_use
break
if j == K - 1:
last_use = (pluged_in, j)
multi.remove(last_use[0])
ans += 1
multi.append(item)
print(ans)운영체제를 공부할 때 페이징 교체 알고리즘들을 공부했었는데 그 중에 최적 교체(OPT, Optimal Replacement)알고리즘과 동일하다. 미래에 사용될 순서를 알아야 한다는 제약 조건 때문에 실제 상용으로 쓰이기는 어렵지만, 이 문제에서는 사용 순서가 입력으로 주어졌기 때문에 최적 교체 알고리즘으로 풀 수 있다.
그리디 문제는 이 문제가 그리디 문제인지 알아내는 것이 포인트인 것 같다.

