세그먼트 트리 - 백준 2042 (22.8.5)

세그먼트 트리란

세그먼트 트리(Segment Tree)는 여러 개의 데이터가 존재할 때 특정 구간의 합(최솟값, 최댓값, 곱 등)을 구하는 데 사용하는 자료구조이다.

특정 구간의 합을 미리 구해둔 후, 요청이 있을 때 이미 구한 합을 활용하여 답을 구하는 것이다.

트리 종류 중에 하나로 이진 트리의 형태이며, 특정 구간의 합을 빠르게$(O(logN))$ 구할 수 있다.

세그먼트 트리 구성

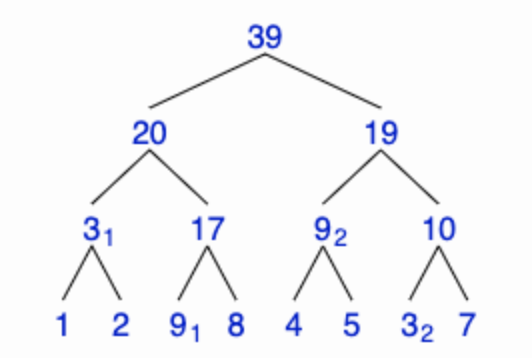구간 합을 구한 이진 트리 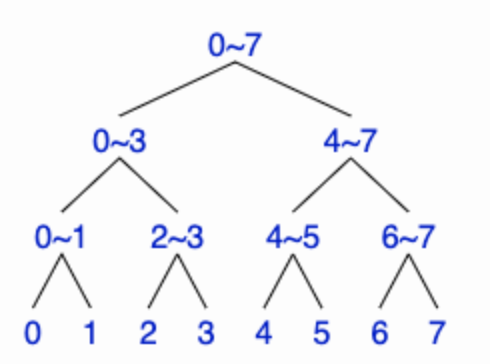각 노드가 포함하고 있는 구간 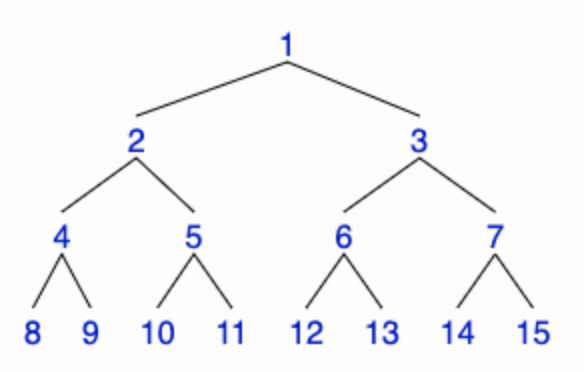세그먼트 트리의 노드 번호

구현 - 백준 2042번 문제

이 문제에서 세그먼트 트리의 구현은 크게 4파트로 나눌 수 있다.

• 세그먼트 트리의 크기 구하기
• 세그먼트 트리 생성
• 구간 합 구하기
• 값 수정하기

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

int N, M, K;
vector<long long> arr;

//세그먼트 트리의 크기는 기존 배열의 크기 n보다 큰 최소의 제곱수 * 2이다
//아니면 이렇게까지 할 필요 없이 그냥 n * 4로 트리 영역을 할당하면 된다
int closest_square(vector<long long> &arr){
    int a = (int)arr.size();
    int i = 1;
    while(1){
        if (pow(i, 2) >= a)
            break;
        i++;
    }
    return pow(i, 2) * 4;
}

//세그먼트 트리 생성 - 구간이 단 하나만 될 때까지 구간을 반으로 나누어 가며 재귀적으로 접근할 수 있다.
long long segment_tree(vector<long long> &tree, int start, int end, int node){
    if (start == end) // 구간이 하나일때
        return tree[node] = arr[start];

    int mid = (start + end) / 2; // 구간을 둘로 나눈뒤 재귀호출
    return tree[node] = segment_tree(tree, start, mid, node*2) + segment_tree(tree, mid+1, end, node*2+1);
}

//부분합 구하기
long long get_sum (vector<long long> &tree, int start, int end, int left, int right, int node){
    if (left > end || right < start) // 구하려는 구간이 현재 구간에 아예 없으면
        return 0;

    if (left <= start && end <= right) // 현재 구간이 구하려는 구간범위 내에 있으면
        return tree[node];

    int mid = (start + end) / 2; // 구하려는 구간이 현재 구간에 걸쳐있으면(하나라도 속해있으면)
    return get_sum(tree, start, mid, left, right, node*2) + get_sum(tree, mid+1, end, left, right, node*2+1);
}

//값 수정하기
void edit_value(vector<long long> &tree, int start, int end, int node, int index, long long value){
    if (index < start || index > end) // 구하려는 인덱스가 현재 구간에 없으면
        return; // 바꿀필요가 없다

    tree[node] += value; // 인덱스가 속해있는 구간이니 수정

    if (start == end) // 인덱스를 정확히 찾으면
        return;
    
    int mid = (start + end) / 2; // 인덱스를 포함하는 구간 재귀탐색
    edit_value(tree, start, mid, node*2, index, value);
    edit_value(tree, mid+1, end, node*2+1, index, value);
}

int main() {
    ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);

    cin >> N >> M >> K;
    arr.push_back(-1); // 인덱스는 1부터 시작하므로
    for (int i = 0; i < N; i++){
        long long tmp;
        cin >> tmp;
        arr.push_back(tmp);
    }
    
    int square = closest_square(arr); // 트리 크기 구하기
    vector<long long> tree(square); // N * 4를 넣어도 된다
    segment_tree(tree, 1, N, 1); // 트리 생성

    for(int i = 0; i < M+K; i++){
        int a, b;
        long long c;
        cin >> a >> b >> c;
        if(a == 1) { // 값 변경
            long long diff = c - arr[b];
            arr[b] = c;
            edit_value(tree, 1, N, 1, b, diff);
        }
        else if (a == 2){
            // 구간 b, c의 합 출력
            cout << get_sum(tree, 1, N, b, c, 1) << '\n';
        }
    }
}