우선순위 큐와 힙 - 백준2696, 골드달성 (22.6.9)

우선순위 큐?

큐(Queue)는 먼저 들어오는 데이터가 먼저 나가는 FIFO(First In First Out) 형식의 자료구조이다.

우선순위 큐(Priority Queue)는 먼저 들어오는 데이터가 아니라, 우선순위가 높은 데이터가 먼저 나가는 형태의 자료구조이다.
우선순위 큐는 일반적으로 힙(Heap)을 이용하여 구현한다.

힙?

힙(Heap)은 우선순위 큐를 위해 고안된 완전이진트리 형태의 자료구조이다.

완전이진트리

마지막 레벨을 제외한 모든 레벨의 node가 완전히 채워져 있으며 마지막 레벨의 node들은 가능한 한 왼쪽부터 채워져 있는 구조를 말한다.

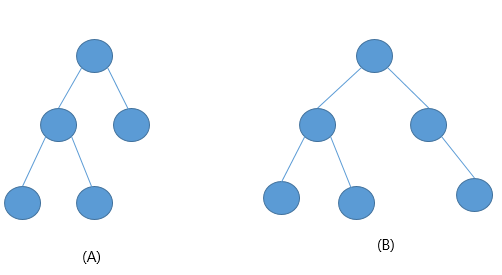
A는 완전이진트리이고 B는 아니다.

힙에는 최소 힙과 최대 힙이 있다.

최대 힙 (Max Heap)

부모 노드의 키 값이 자식 노드보다 크거나 같은 완전이진트리이다.
❝ key(부모노드) ≥ key(자식노드) ❞

최소 힙 (Min Heap)

부모 노드의 키 값이 자식 노드보다 작거나 같은 완전이진트리이다.
❝ key(부모노드) ≥ key(자식노드) ❞


자식노드를 구하고 싶을 때

왼쪽 자식노드 index = (부모 노드 index) 2
오른쪽 자식노드 index = (부모 노드 index) 2 + 1

부모노드를 구하고 싶을 때

부모 노드 index = (자식노드 index) / 2

삽입 연산

힙에 삽입을 하기 위해서는 힙 트리의 성질을 만족시키면서 새로운 요소를 추가해야 한다.

우선 완전이진트리의 마지막 노드에 이어서 새로운 노드를 추가한다.
추가된 새로운 노드를 부모의 노드와 비교하여 교환한다.
정상적인 힙트리가 될 때 까지 (더이상 부모노드와 교환할 필요가 없을 때까지) 2번을 반복한다.

최악의 경우 새로 추가된 노드가 루트노트까지 비교하며 올라가야 하므로 시간복잡도가 O(log₂n)이다.

삭제 연산

힙 트리에서 루트노드가 가장 우선순위가 높으므로 루트 노드를 삭제해야 한다.

삭제가 이뤄진 후 힙 트리의 성질이 유지돼야 하므로 아래와 같은 방법으로 삭제를 진행한다.

루트 노드를 삭제한다.
루트 노드가 삭제된 빈자리에 완전이진트리의 마지막 노드를 가져온다.
루트 자리에 위치한 새로운 노드를 자식 노드와 비교하여 교환한다.
이때 최대 힙인 경우 자식노드 중 더 큰 값과 교환을 하며, 최소 힙인 경우 더 작은 값과 교환을 한다.
정상적인 힙트리가 될 때까지 (더 이상 자식노드와 교환할 필요가 없을 때까지) 3번을 반복한다.

삭제 연산 또한 최악의 경우 루트노트부터 가장 아래까지 내려가야 하므로 시간복잡도가 O(log₂n)이다.

백준 2696 문제

문제
어떤 수열을 읽고, 홀수번째 수를 읽을 때 마다, 지금까지 입력받은 값의 중앙값을 출력하는 프로그램을 작성하시오.

예를 들어, 수열이 1,5,4,3,2 이면, 홀수번째 수는 1번째 수, 3번째 수, 5번째 수이고, 1번째 수를 읽었을 때 중앙값은 1, 3번째 수를 읽었을 때는 4, 5번째 수를 읽었을 때는 3이다.

입력
첫째 줄에 테스트 케이스의 개수 T(1<=T<=1,000)가 주어진다. 각 테스트 케이스의 첫째 줄에는 수열의 크기 M(1<=M<=9999, M=홀수)이 주어지고, 그 다음 줄부터 이 수열의 원소가 차례대로 주어진다. 원소는 한 줄에 10개씩 나누어져있고, 32비트 부호있는 정수이다. (대부분의 언어에서 int)

출력
각 테스트 케이스에 대해 첫째 줄에 출력하는 중앙값의 개수를 출력하고, 둘째 줄에는 홀수 번째 수를 읽을 때 마다 구한 중앙값을 차례대로 공백으로 구분하여 출력한다. 이때, 한 줄에 10개씩 출력해야 한다.

예제 입력

3
9
1 2 3 4 5 6 7 8 9
9
9 8 7 6 5 4 3 2 1
23
23 41 13 22 -3 24 -31 -11 -8 -7
3 5 103 211 -311 -45 -67 -73 -81 -99
-33 24 56

예제 출력

5
1 2 3 4 5
5
9 8 7 6 5
12
23 23 22 22 13 3 5 5 3 -3
-7 -3

풀이

import heapq
import sys
input = sys.stdin.readline

for _ in range(int(input())):
    lhq = [] # 중앙값 이하들 최대힙
    rhq = [] # 중앙값 초과들 최소힙
    ans = []
    for i in range((int(input()) - 1) // 10 + 1):
        for j, num in enumerate(map(int, input().split())):
            if not lhq: # 맨첫값은 그냥 푸쉬
                heapq.heappush(lhq, -num)
                ans.append(num)
                continue

            if -lhq[0] >= num: #중앙값보다 작을시 최대힙에 추가
                if len(lhq) > len(rhq):
                    heapq.heappush(rhq, -heapq.heappop(lhq)) # 왼쪽크기 <= 오른쪽크기 < 왼쪽크기 + 1 을 유지
                heapq.heappush(lhq, -num) # 주의할점 !!! 나중에 푸쉬를 해야함 

            else: #크면 최소힙에 추가
                heapq.heappush(rhq, num) # 주의할점 !!! 먼저 푸쉬를 해야한다. 이거 찾느라 30분걸렸다
                if len(lhq) <= len(rhq):
                    heapq.heappush(lhq, -heapq.heappop(rhq))

            if not j & 1: # 짝수번째만 출력
                ans.append(-lhq[0])
                
    print(len(ans))
    for i, val in enumerate(ans):
        if not i % 10 and i > 0:
            print()
        print(val, end = " ")
    print()

직관적인 방법으로 2번에 한번씩 정렬하면서 풀면 시간복잡도가 $O(M^2logM)$ 인데, M의 최댓값이 거의 1만이므로 좀 불안하니 다른 방법으로 푸는게 좋다. 우선순위 큐를 이용해서 풀 수 있다.

항상 중앙값과 그 왼쪽값들은 최대 힙에, 오른쪽 값들은 최소힙에 저장되도록 유지하면, 언제나 최대힙의 루트에 중앙값이 위치하게 된다.

우선순위 큐에서 삽입이나 삭제는 $O(logM)$이고, 이것을 M번 반복하면 $O(MlogM)$이므로 정렬만 이용하는 방법보다 빠르다.

잡담

알고리즘 공부 시작 $2^5$일째.. 골드를 달성했다!
티어시스템이 있는게 은근 동기부여가 되는 것 같다.
목표인 플래티넘까지 얼마나 걸릴까..? 복학하면 알고리즘 강의를 들을 예정인데 그 전까지 달성하면 좋겠다. 그러면 A+받을 수 있겠지?