[알고리즘] 다익스트라(Dijkstra)

gif 출처: https://tinyurl.com/y287lhew

다익스트라(Dijkstra) 알고리즘이란?

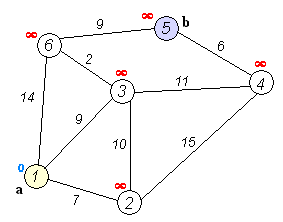
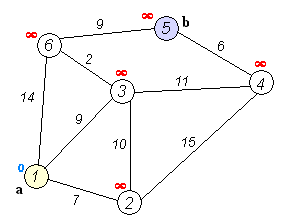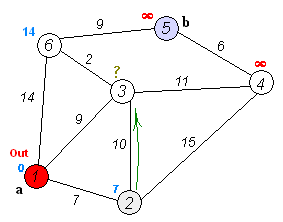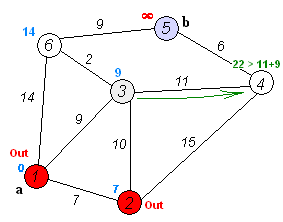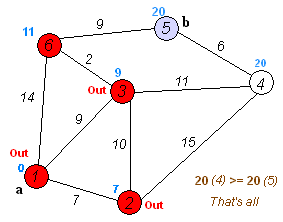
🗺 그래프 중 출발점에서 목표점까지의 최단거리를 구할 때 사용하는 알고리즘.

필요한 변수

int distance[] = new int[n+1];
boolean[] check = new boolean[n+1];

distance는 각각의 노드까지의 최단거리가 저장된다.
check는 각각의 노드를 방문 했는지를 표시하고 저장한다.

순서

1. distance는 처음에 나올 수 있는 가장 큰 값으로 초기화 해준다.

2. 시작 노드의 거리를 0으로 표시한다.(자기 자신)
   그리고 시작 노드의 check값을 true로 바꾼다.(자신은 이미 방문)

3. 시작 노드와 연결되어 있는 노드들의 distance 값들을 갱신한다.

4. 방문하지 않는 노드 중 distance 값이 최소인 min_node를 찾는다.

5. min_node의 check값을 true로 변경한다.(해당 노드로 이동했다는 의미)
   그리고 min_node와 연결된 방문하지 않은 노드들의 distance 값들을 갱신한다.
   이때,
   min_node와 연결된 distance 값이
   distance[min_node] + (min_node와 연결 노드의 거리)보다 큰 경우,
   distance 값을 [min_node] + (min_node와 연결 노드의 거리)로 갱신해준다.

4~5 번을 모든 노드를 방문할 때까지 반복한다.

구현

다익스트라 클래스

class Graph {
	private int n;
	private int maps[][];

	public Graph(int n) {
		this.n = n;
		maps = new int[n + 1][n + 1];
	}

	public void input(int i, int j, int w) {
		maps[i][j] = w;
		maps[j][i] = w;
	}

	public void dijkstra(int v) {
		int distance[] = new int[n + 1];
		boolean[] check = new boolean[n + 1];
		for (int i = 1; i < n + 1; i++) {
			distance[i] = Integer.MAX_VALUE;
		}
		distance[v] = 0;
		check[v] = true;
		for (int i = 1; i < n + 1; i++) {
			if (!check[i] && maps[v][i] != 0) {
				distance[i] = maps[v][i];
			}
		}
		for (int a = 0; a < n - 1; a++) {
			int min = Integer.MAX_VALUE;
			int min_index = -1;
			for (int i = 1; i < n + 1; i++) {
				if (!check[i] && distance[i] != Integer.MAX_VALUE) {
					if (distance[i] < min) {
						min = distance[i];
						min_index = i;
					}
				}
			}
			check[min_index] = true;
			for (int i = 1; i < n + 1; i++) {
				if (!check[i] && maps[min_index][i] != 0) {
					if (distance[i] > distance[min_index] + maps[min_index][i]) {
						distance[i] = distance[min_index] + maps[min_index][i];
					}
				}
			}
		}
		for (int i = 1; i < n + 1; i++) {
			System.out.print(distance[i] + " ");
		}
		System.out.println("");
	}
}

메인 메소드

public class Main {
	public static void main(String[] args) {
		Graph g = new Graph(8);
		g.input(1, 2, 3);
		g.input(1, 5, 4);
		g.input(1, 4, 4);
		g.input(2, 3, 2);
		g.input(3, 4, 1);
		g.input(4, 5, 2);
		g.input(5, 6, 4);
		g.input(4, 7, 6);
		g.input(7, 6, 3);
		g.input(3, 8, 3);
		g.input(6, 8, 2);
		g.dijkstra(1);
	}
}

Reference

• 범범스(tistory)