재귀 알고리즘

---

• 어떤 사건이 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의될 때 재귀적이라고 한다.

유클리드 호제법

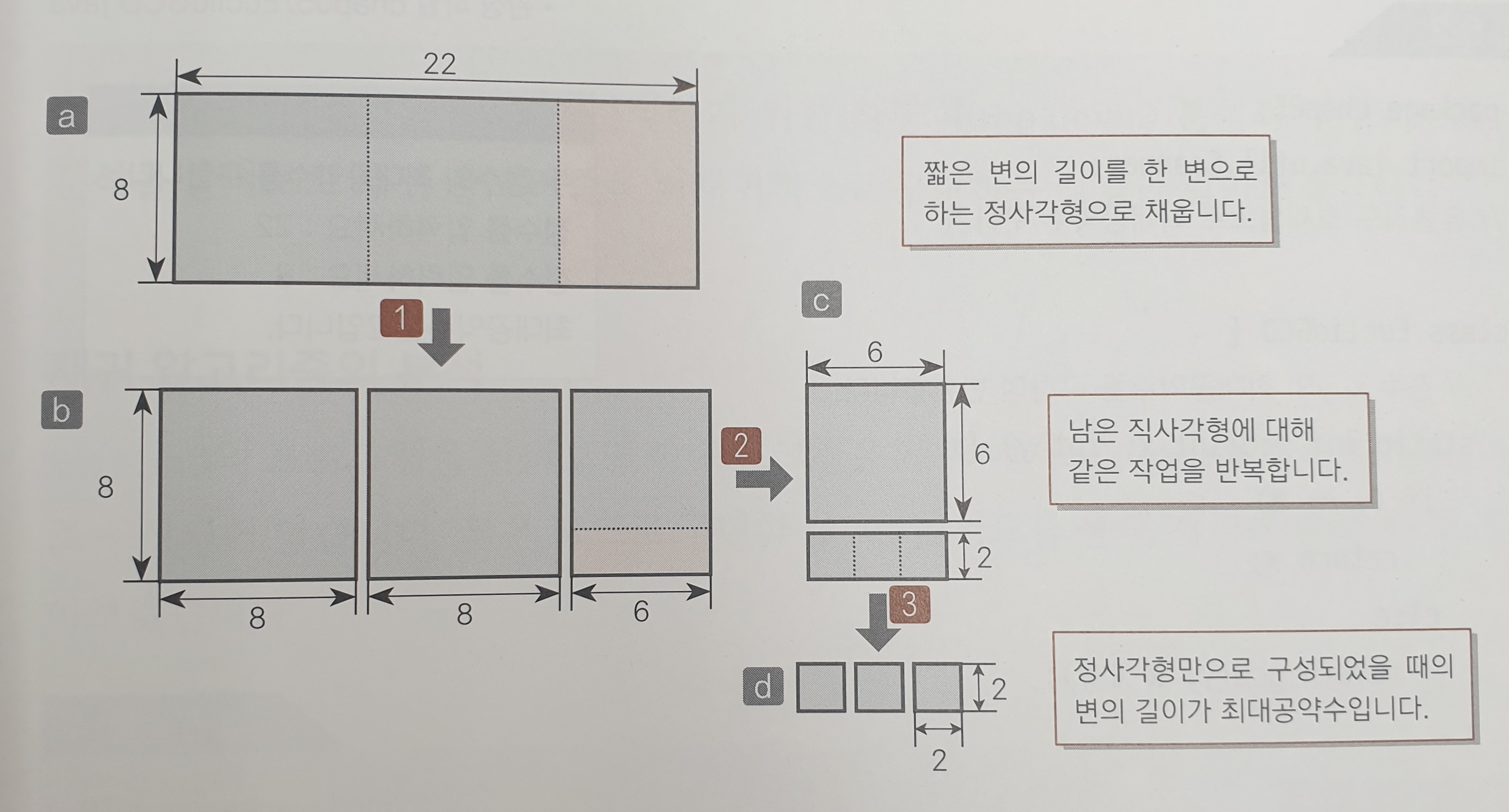
• 두 정수의 최대공약수는 두 정수를 변으로 하는 직사각형을 위의 방법처럼 채워나가다보면 정사각형만으로 구성되게 할 수 있다. 이 정사각형의 길이가 최대공약수이다.

static int gcd(int x, int y) {
  if (y == 0) // 변의 길이가 x인 정사각형일 때
    return x;
  else
    return gcd(y, x % y); // 짧은변이 긴변이 되고, 긴변을 짧은변으로 나눈값이 짧은변이 된다.
}

gcd(22, 8) // 최대공약수는 2

분석

static void recur(int n) {
  if(n > 0) {
    recur(n - 1);
    System.out.println(n);
    recur(n - 2);
  }
}

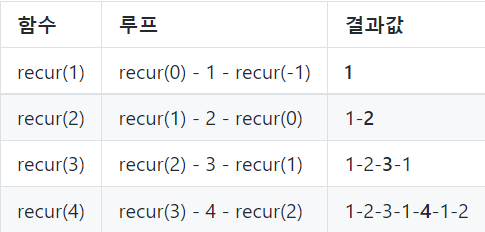
하향식 분석

• recur(4)를 구하려고 했을 때, 매개변수에 곧바로 4를 넣어서 순서대로 분석하면 된다.
  

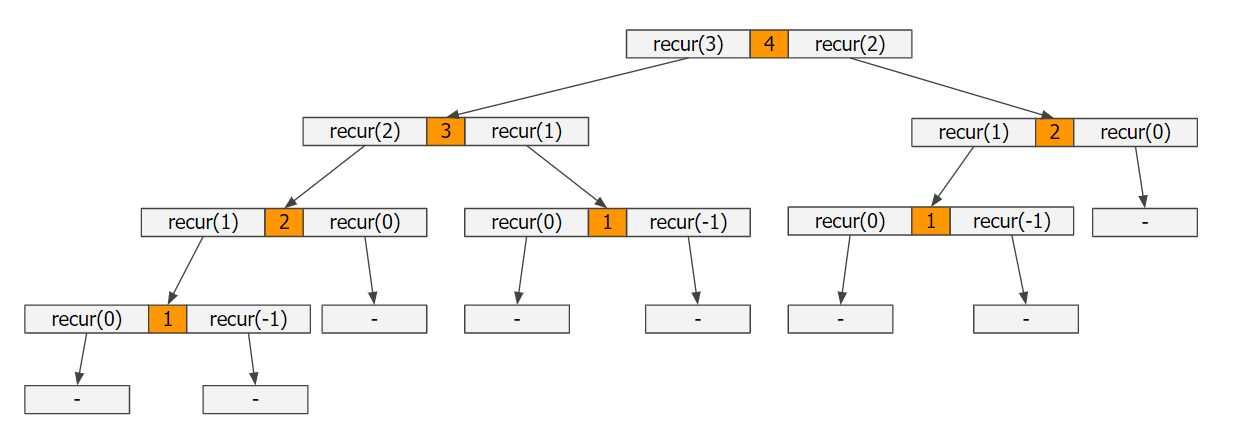
상향식 분석

• recur(4)를 구하려고 했을 때, if문 조건이 양수이므로 recur(1)부터recur(4)까지 구해나가는 방법이다.
  

재귀 알고리즘의 비재귀적 표현

---

꼬리 재귀의 제거

• 메서드의 꼬리에 있는 recur(n-2)는 n의 값을 n-2로 업데이트하고 메서드의 시작 지점으로 돌아가라는 말과 동일하다.

static void recur(int n) {
  while(n > 0) {
    recur(n - 1);
    System.out.println(n);
    n = n - 2;
  }
}

재귀의 제거

• 앞에서 호출한 재귀 메서드는 n을 출력하기 전에 recur(n-1)을 먼저 수행한다. 따라서 n의 값을 잠시 저장할 수 있는 스택이나 배열을 사용해야 한다.

static void recur(int n) {
  IntStack s = new IntStack(n);
		
  while(true) {
    if (n > 0) {
      s.push(n);
      n = n - 1;
      continue;
    }
    if (s.isEmpty() != true) {
      n = s.pop();
      System.out.println(n);
      n = n - 2;
      continue;
    }
    break;
  }
}

하노이의 탑

---

• 제일 아래에 있는 원판을 1번, 그 위에 있는 원판들을 2번이라고 해보자.
• 그러면 2번을 먼저 다른 기둥에 옮기고 1번을 목적지 기둥에 옮긴 후 2번을 목적지 기둥으로 옮기는 과정을 반복하는 것이 핵심 개념이다.

satic void move(int no, int x, int y) {
  if(no > 1)
    move(no - 1, x, 6 - x - y);
  System.out.println("원반[" + no + "]을" + x + "기둥에서 " + y + "기둥으로 옮김");
  if(no > 1)
    move(no - 1, 6 - x - y, y);
}
move(n, 1, 3); // 1번 기둥의 n개의 원반을 3번 기둥으로 옮김

8퀸 문제

---

• 가우스가 잘못된 해답을 낸 것으로 유명한 8퀸 문제는 재귀 알고리즘에 대한 예제로 자주 등장한다.
• 열의 중복 제거 -> 행의 중복 제거 -> 대각선의 중복제거 순으로 차례대로 구현한다.

static boolean[] flag_a = new boolean[8];
// 해당 행에 배치가 되어있는지 확인하는 용도
static boolean[] flag_b = new boolean[15];
static boolean[] flag_c = new boolean[15];
// 두 대각선 방향에 배치가 되어있는지 확인하는 용도
static int[] pos = new int[8];
// pos[열] = 행의 형태로 입력, 해당 열에 배치가 되어있는지 확인하는 용도
	
static void set(int i) {
  for (int j = 0; j < 8; j++) {
    if (flag_a[j] == false && flag_b[i + j] == false && flag_c[i - j + 7] == false) {
      pos[i] = j;
      if (i == 7)
      // 모든 열에 배치할 경우 출력
        print();
      else {
        flag_a[j] =  flag_b[i + j] = flag_c[i - j + 7] = true;
        set(i + 1);
        flag_a[j] =  flag_b[i + j] = flag_c[i - j + 7] = false;
        // print 한 후 배치여부 flase로 변경
      }
    }
  }
}

set(0);