정렬
- 정렬이란 이름, 학번 등 핵심 항목(key)의 대소 관계에 따라 데이터 집합을 일정한 순서로 줄지어 늘어서도록 바꾸는 작업을 말한다.
- 키 값이 작은 데이터가 앞쪽에 있는 것이 오름차순, 반대로 있는 것이 내림차순이다.
- 정렬 알고리즘의 핵심 요소는 교환, 선택, 삽입이며 대부분의 정렬 알고리즘은 이 세가지 요소를 응용한 것이다.
안정성
- 정렬 알고리즘은 안정된 알고리즘과 그렇지 않은 알고리즘으로 나눌 수 있다.
- 안정된 정렬이란 같은 값의 키를 가진 요소의 순서가 정렬하더라도 유지된 것을 말한다.
내부 정렬과 외부 정렬
- 내부 정렬 : 정렬할 모든 데이터를 하나의 배열에 저장할 수 있는 경우에 사용하는 알고리즘
- 외부 정렬 : 정렬할 데이터가 너무 많아서 하나의 배열에 저장할 수 없는 경우에 사용하는 알고리즘
- 외부 정렬은 내부 정렬을 응용한 것으로, 외부 정렬을 구현하려면 작업을 위한 파일 들이 필요하고 알고리즘도 복잡하다.
- 이 책에서는 내부 정렬만 다룬다.
버블 정렬
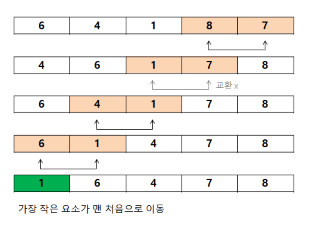
- 위처럼 이웃한 요소를 비교하고 교환하는 작업을 한바퀴 실행하면 첫 번째 요소가 정렬된다. 이를 총 n-1회 실행하면 배열이 오름차순으로 정렬되며, 이런 정렬을 버블 정렬이라고 한다.
기본 코드
// a[idx1]와 a[idx2]의 값을 바꾸는 함수
static void swap(int[] a, int idx1, int idx2) {
int i = a[idx];
a[idx1] = a[idx2];
a[idx2] = t;
}
// 버블 정렬
static void bubbleSort(int[] a, int n) {
for (int i = 0; i < n - 1; i++) {
// n-1번의 정렬 수행
for (int j = n - 1; j > i; j--)
// 배열의 끝에서부터 정렬된 요소의 인덱스 + 1에 도달하기 전까지 실행
// j - 1과 j 번째의 요소를 비교하기 때문에 인덱스 + 1까지 실행함.
if(a[j - 1] > a[j])
swap(a, j - 1; j);
}
}개선된 코드
- 비교, 교환을 하다가 이떤 시점 이후에 교환이 수행되지 않는다면 그보다 앞쪽의 요소는 이미 정렬을 마친 상태라고 생각한다.
- 처음 실행을 했을 때 교환이 전혀 실행되지 않는 경우는 이미 정렬되어 있는 상태로 볼 수 있기 때문에 실행이 종료된다.
static void bubblesort(int[] a, int n) {
int k = 0; // a[k]보다 앞쪽은 정렬을 마친 상태
while (k < n - 1) {
int last = n - 1;
for (int j = n - 1; j > k; j--)
if (a[j - 1] > a[j]) {
swap(a, j - 1, j);
last = j; // 교환이 진행될 때 마다 해당 인덱스를 저장한다.
}
}
}단순 선택 정렬
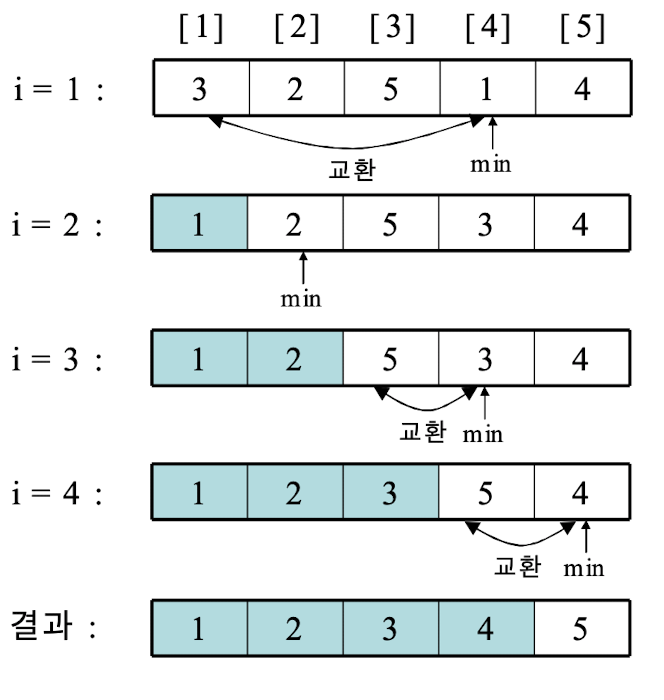
- 가장 작은 요소를 첫번째 위치의 요소과 교환한다. 그 다음 작은 요소를 두번째 위치의 요소와 교환한다. 이를 총 n - 1번 실행하면 배열이 정렬된다.
- 이런 정렬을 선택 정렬이라고 하며, 교환 과정은 다음과 같다.
- 아직 정렬하지 않은 부분에서 가장 작은 키의 값을 선택한다.
- 해당 요소와 아직 정렬하지 않은 부분의 첫번째 요소와 교환한다.
- 이 과정을 n - 1번 반복한다.
- 서로 떨어져 있는 요소를 교환하기 때문에 안정적이지 않다.
코드
static void selectionSort(int[] a, int n) {
for (int i = 0; i < n - 1; i++) {
int min = i;
for (int j = i + 1; j < n; j++)
if (a[j] < a[min])
min = j;
swap(a, i, min);
}
}단순 삽입 정렬
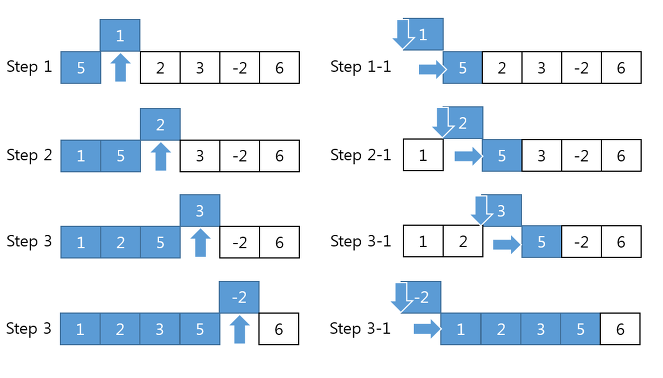
- 정렬되지 않는 부분의 첫 번째 요소를 정렬된 부분의 알맞는 위치에 삽입한다. 이를 총 n-1회 실행하면 배열이 정렬된다.
- 버블, 선택, 삽입 정렬의 시간 복잡도는 O(n^2)이다.
코드
static void insertionSort(int[] a, int n) {
for (int i = 1; i < n; i++) {
int j;
int tmp =a[i];
for (j = i; j > 0 && a[j - 1] > tmp; j--)
a[j] = a[j - 1];
a[j] = tmp;
}
}셸 정렬
- 셸 정렬은 단순 삽입 정렬의 장점은 살리고 단점은 보완한 정렬 알고리즘이다.
- 단순 삽입 정렬의 장점 : 정렬을 마쳤거나 정렬을 마친 상태에 가까우면 정렬 속도가 매우 빨라진다.
- 단순 삽입 정렬의 단점 : 삽입할 위치가 멀리 떨어져 있으면 이동(대입)해야 하는 횟수가 많아진다.
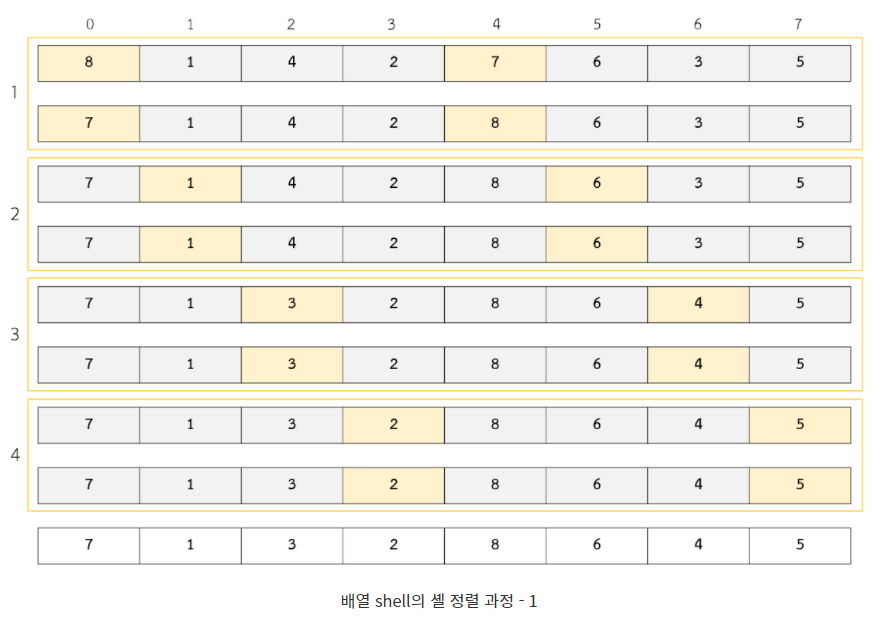
- 처음에는 총 요소의 절반인 4칸만큼 떨어진 2개의 요소를 정렬한다.
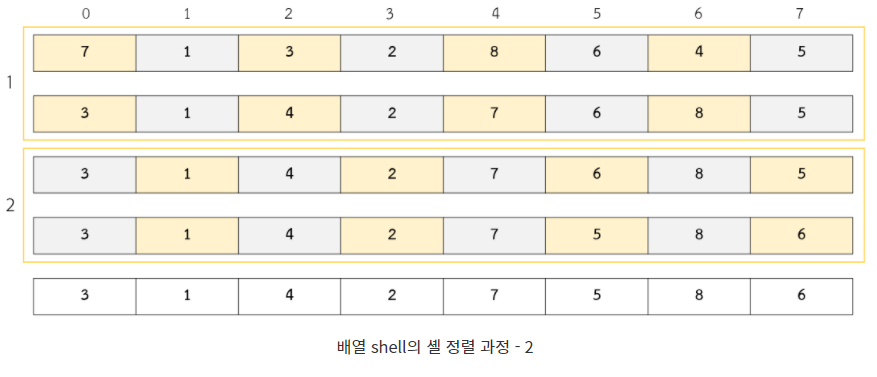
- 그 다음에는 4칸의 절반인 2칸만큼 떨어진 4개의 요소를 정렬한다. 마지막으로 1칸만큼 떨어진 8개 요소를 정렬한다.
- 여러 그룹으로 나누어 정렬하는 이유는 단순 삽입 정렬의 장점은 살리고 단점은 보완이 되기 때문이다.
- 위에서는 증분값(h)을 절반으로 나눈 4, 2, 1로 했다. 하지만 증분값을 3h + 1의 수열로 하고 배열의 요솟수를 9로 나눈 값을 넘지 않도록 하는 것이 더 효율적이다.
- 시간 복잡도는 O(n^1.25)이며, 안정적이진 않다.
코드
static void shellShort(int[] a, int n) {
int h;
for (h = 1; h , n / 9; h = h * 3 + 1)
// 증분값 선정
;
for ( ; h > 0; h /= 3)
for (int i = h; i < n; i++) {
int j;
in tmp = a[i];
for (j = i - h; j >= 0 && a[j] > tmp; j -= h)
a[j + h] = a[j];
a[j + h] = tmp;
}
}
do for me