퀵 정렬

---

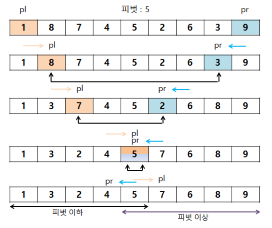
• 일반적으로 사용되고 있는 아주 빠른 정렬 알고리즘이다.
• 시간 복잡도는 평균적으로 n log n이지만, 최악의 경우 O(n^2)이다.

원리

• 피벗이라고 부르는 기준이 될 임의의 값을 선택한다.
• 피벗 이하의 그룹, 피벗 이상의 그룹으로 나눈다.
• 두 그룹에서 다시 각각의 피벗을 선정하고 그룹을 쪼갠다.
• 이를 반복하면 정렬된다.

코드

static void quickSort(int[] a, int left, int right) {
  int pl = left;
  int pr = right;
  int x = a[(pl + pr) / 2]; // 피벗
  
  dp {
    while (a[pl] < x) pl++;
    while (a[pr] > x) pr--;
    if (pl <= pr)
      swap(a, pl++, pr--);
  } while (pl <= pr); // 피벗을 기준으로 그룹이 나뉘면 false가 된다.
  
  if (left < pr) quicksort(a, left, pr);
  if (pl < right) quickSort(a, pl, righ);
}

• 코드에서는 피벗을 중간값으로 했지만, 실행 효율을 높일 수 있는 방법이 있다.
• 나눌 배열의 처음, 가운데, 끝 요소를 정렬한 다음 가운데 요소와 끝에서 두번째 요소를 교환한다.
  • 세 요소를 선택하고 그 중에서 가운데 요소를 택하면 신뢰도가 더 높다.
  • 세 요소는 분류되므로 이들을 빼고 정렬을 수행하면 된다.

병합 정렬

---

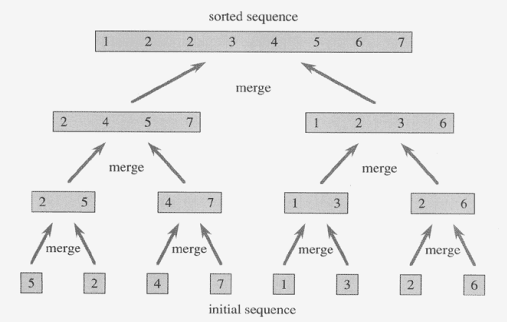
• 배열을 앞부분과 뒷부분으로 나누어 각각 정렬한 다음 병합하는 작업을 반복하여 정렬을 수행하는 알고리즘이다.
• 시간 복잡도는 O(n log n)이며, 안정적이다.

코드

static int[] buff;
buff = new int[n];

static void mergeSort(int[] a, int left, int right) {
  if (left < right) {
    int i;
    int center = (left + right) / 2;
    int p = 0;
    int j = 0;
    int k = left;
    
    mergeSort(a, left, center);
    mergeSort(a, center + 1, right);
    
    // a의 왼쪽 그룹을 buffer에 복사
    for (i = left; i <= center; i++)
      buff[p++] = a[i];
      
    // a의 오른쪽 그룹이 끝나기 전 and buffer가 끝나기 전까지
    while (i <= right && j < p)
      // 두 그룹을 비교하여 작은 값을 a의 처음부터 삽입
      a[k++] = (buff[j] <= a[i]) ? buff[j++] : a[i++];
      
    // buffer의 요소가 남아있는 경우 a에 삽입
    while (j < p)
      a[k++] = buff[j++];
  }
}

buff = null;