컴퓨터구조 4강 - 조합논리회로

soo·2022년 7월 24일

CS 강의기록 컴퓨터구조

0

컴퓨터구조

목록 보기

4/6

학습 목표

조합 논리회로의 동작 표현 방법인 논리식, 진가표, 논리회로도를 해석할 수 있다.
가산기, 비교기, 패리티 발생/검사기, 인코더/디코더, 멀티플렉서/디멀티플렉서의 기능을 설명할 수 있다.

내용

4.1 조합 논리회로 소개
4.2 산술 조합 논리회로
4.3 조합 논리회로 빌딩블록

4.1 조합 논리회로 소개

📍 조합 논리회로 (combinational logic circuit)

입력 조합에 따라 출력을 결정하는 논리회로
입력 값의 조합 일정 👉 출력도 일정

학습 목표

조합 논리회로의 동작을 표현한느 법 이해
진가표, 논리식, 논리회로도 표현 방법 숙달

내용

4.1.1 조합 논리회로 동작 표현: 진가표, 논리식, 논리회로도
4.1.2 최소항: 진가표 ➡️ 논리회로도
4.1.3 무관조건(don't care condition): 동작에 영향을 주지 않는 논리값

4.1.1 조합 논리회로의 동작 표현

📍 동작 표현 방법

진가표 = 동작 특성표 = 특성표(characteristic table)
논리식(logic equation) = 부울식(Bool equation) = 논리함수(logic function)
논리 회로도(logic diagram)
nXm 조합 논리회로의 진가표 (입력은 n비트, 출력은 m비트인 논리회로의 진가표)
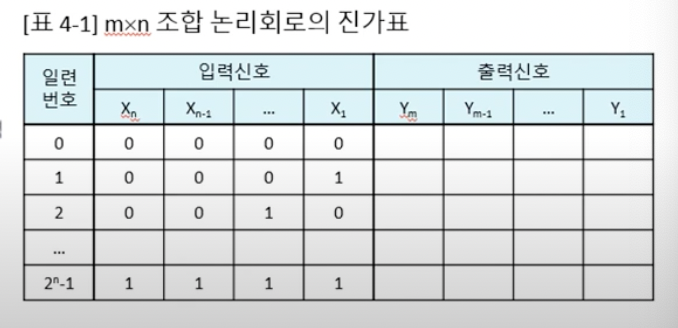
진가표는 입력신호의 값을 전부 적어야 함 👉 0 ~ 2^n-1까지 총 2^n개의 열
일련번호, 입력신호를 모두 일반적으로는 이진수의 순서로 적음
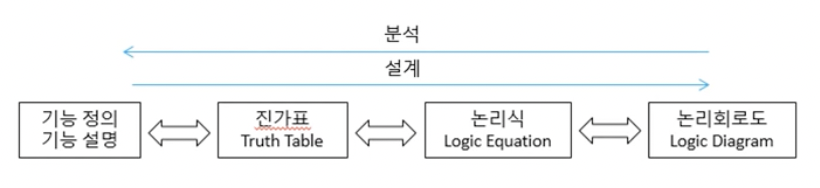
설명 순서
(1) 논리식 ➡️ 논리회로도 직관적 논리회로도 ➡️ 논리식
(3) 논리식 ➡️ 진가표
(4) 진가표 ➡️ 논리식: 최소항(또는 최대항)에 의한 방법 [어려움]

📍 논리식 ➡️ 논리회로도

논리식의 연산 우선 순위: 괄호() > NOT(') > AND > OR
논리회로도 그리는 법

입력신호를 왼편에, 출력신호를 오른편에 배치한다.
연산 우선 순위에 따라 입력에서 출력 방향으로 게이트를 배치하고 입력과 출력을 연결한다.

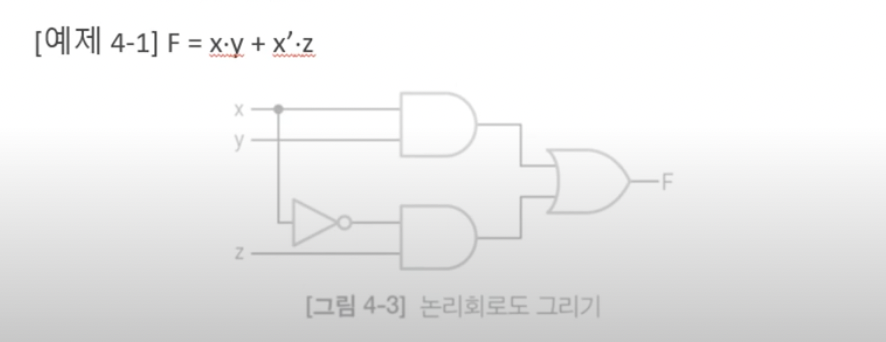
NOT이 우선순위 1위이므로 가장 먼저 그림 ➡️ AND 게이트 그림(x*y, x'*z)

📍 논리회로도 ➡️ 논리식

논리식 구하는 방법

입력, 출력, 게이트의 출력에 논리 변수 할당
입력단부터 출력단 방향으로 게이트의 논리식 적기
출력단에 포함된 게이트의 출력을 입력 신호의 논리식으로 대치

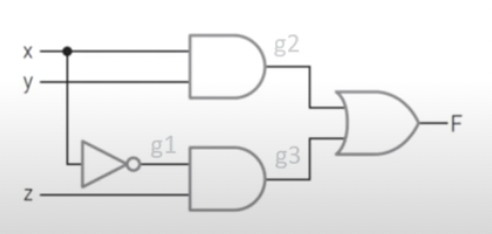
이 회로의 논리식: x*y + x'*z
(1) 입력과 출력, 게이트 출력에 이름을 부여한다 (왼쪽부터 g1, g2, g3)
(2) 게이트 출력 논리식을 구한다.
g1 = x'
g2 = x*y
g3 = g1*z
F = g2 + g3
(3) 출력 논리식에 포함된 게이트 출력을 입력신호로 대치한다.
F = g2 + g3 = x*y + g1*z = x*y + x'*z

📍 논리식 ➡️ 진가표

방법

모든 입력 신호의 조합을 이진수 순서로 표에 배치
논리식의 연산 우선순위에 따라 세부 항에 대한 출력을 구한다.

예제) F = x*y + x'*z

x	y	z	x'	x*y	x'*z	F
0	0	0	1	0	0	0
0	0	1	1	0	1	1
0	1	0	1	0	0	0
0	1	1	1	0	1	1
1	0	0	0	0	0	0
1	0	1	0	0	0	0
1	1	0	0	1	0	1
1	1	1	0	1	0	1

4.1.2 최소항

📍 진가표로부터 논리식을 구하는 두 가지 방법

논리곱(AND)의 합(OR)(sum of products)으로 표현하는 방법
논리합(OR)의 곱(AND)(products of sum)으로 표현하는 방법 (서로 쌍대)

📍 논리곱과 최소항

논리곱: 논리변수들이 AND 연산으로 묶인 항
최소항(minterm): 논리변수들이 모두 참여하는 논리곱
예) 입력변수가 x, y, z일 때
논리곱의 예: x, y, yz, x'y'z', xy'z' 등
최소항의 예: x'y'z', x'yz, xy'z 등

📍 곱항의 합(sum of products)

F1(x,y,z) = x + yz
F2(x,y,z) = xy + x'z
F3(x,y,z) = x'y'z + xyz 👉 논리곱의 합
진가표로부터 논리식 구할 때는

최소항을 먼저 구함
이중에서 인접항을 찾아 간소화

📍 최소항

입력 신호의 조합 중에서 출력이 하나만 1인 논리함수
입력변수가 모두 참여하는 AND항

x	y	z	$m_0$ (x'y'z')	$m_1$ (x'y'z)	$m_2$ (x'yz')	$m_3$ (x'yz)	$m_4$ (xy'z)'	$m_5$ (xy'z)	$m_6$ (xyz')	$m_7$ (xyz)
0	0	0	1	0	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	0
0	1	0	0	0	1	0	0	0	0	0
0	1	1	0	0	0	1	0	0	0	0
1	0	0	0	0	0	0	1	0	0	0
1	0	1	0	0	0	0	0	1	0	0
1	1	0	0	0	0	0	0	0	1	0
1	1	1	0	0	0	0	0	0	0	1

m0: 모두 0일 때만 출력이 1인 진가표를 갖는 논리함수

📍 최소항의 합으로 논리식 구하기

1단계: 진가표에 대한 논리식을 최소항의 합으로 표현
2단계: 간소화(부울대수, 인접항 찾기)
예제) 진가표에 대한 논리식 [중간에 생략!!]

x	y	z	F	$m_1$	$m_3$	$m_6$	$m_7$
0	0	0	0	0	0	0	0
0	0	1	1	1	0	0	0
0	1	0	0	0	0	0	0
0	1	1	1	0	1	0	0
1	0	0	0	0	0	0	0
1	0	1	0	0	0	0	0
1	1	0	1	0	0	1	0
1	1	1	1	0	0	0	1

우선 최소항의 합으로 분해 👉 1이 있는 조합 한 개씩마다 $m_1$ 만 1이고 나머지는 0인 조합
(1) 최소항의 합
F(x,y,z) = m1 + m3 + m6 + m7 = x'y'z + x'yz + xyz' + xyz
(2) 간소화
F(x,y,z) = x'z + xy

4.1.3 무관조건

📍 무관조건(don't care condition)

특정한 입력 신호 조합이 절대로 발생하지 않거나
입력 신호에 대한 출력이 회로의 동작에 영향을 주지 않는 조건
진가표에 x 또는 d로 표현
예) 디코더 진가표

입력	출력
Enable	D1	D0	Y3	Y2	Y1	Y0	Valid
0	x	x	x	x	x	x	0
1	0	0	0	0	0	1	1
1	0	1	0	0	1	0	1
1	1	0	0	1	0	0	1
1	1	1	1	0	0	0	1

Enable 0: 입력이 0이건 1이건 상관이 없다.
Enable이 0이면 valid 또한 1이 됨 = 출력도 상관 없다.
상관 없으면 x로 표시
0-9까지 표시하는 7-Segment 표시 장치에서 0-9가 아닌 A-F의 숫자는 전부 don't care condition

4.2 산술 조합 논리회로

학습 목표

조합논리회로로 만든 산술 회로의 동작 이해

내용

4.2.1 가산기(adder)
4.2.2 비교기(comparator)
4.2.3 패리티 발생기/검사기(parity generator/checker)

4.2.1 가산기

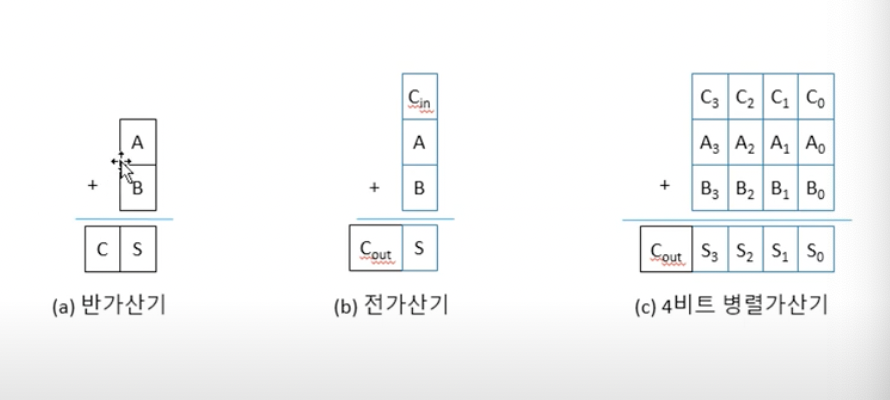
가산기 중 가장 간단한 것 = 한 비트를 더하는 것 (반가산기)
합(sum)과 캐리(Carry - 자리올림수)를 만들어내는 것
전가산기: A와 B 한 비트를 더하는데 아랫단에서 전달되는 자리올림수(carry in)까지 더해서 합과 캐리(carry out)을 만들어내는 가산기
4비트 병렬계산기: 앞쪽을 더할 때는 전가산기, 맨 끝쪽(오른)을 더할 때는 반가산기를 쓰는 것

📍 반가산기 (half adder)

두 비트를 더해서
합과 자리올림수를 계산하는 회로

입출력 변수

입력: A, B
출력: S(sum), C(carry)

진가표

A	B	C	S	설명
0	0	0	0	0 + 0 = 00
0	1	0	1	0 + 1 = 01
1	0	0	1	1 + 0 = 01
1	1	1	0	1 + 1 = 10

논리식

S = _A xor B
C = _A and B

논리회로도

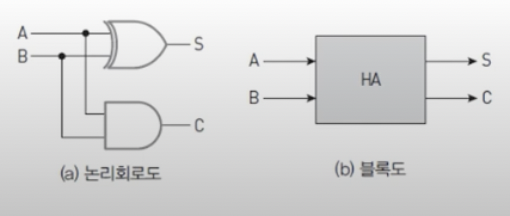
📍 전가산기 (full adder)

한 비트 2진수 두 개(A, B)와 아랫단에서 발생한 자리올림수( $C_{in}$ )까지 세 비트를 더해서 합(S)과 자리올림수( $C_{out}$ )를 계산하는 회로

입출력 변수

입력: A, B, $C_{in}$ (carry in)
출력: S(sum), $C_{out}$ (carry out)
진가표

A	B	$C_{in}$	$C_{out}$	S	설명
0	0	0	0	0	0+0+0=00
0	0	1	0	1	0+0+1=01
0	1	0	0	0	0+1+0=01
0	1	1	0	1	0+1+1=10
1	0	0	0	1	1+0+0=01
1	0	1	1	0	1+0+1=10
1	1	0	1	0	1+1+0=10
1	1	1	1	1	1+1+1=11

논리식

S = A+B+ $C_{in}$ = (A+B) + $C_{in}$
$C_{out}$ (carry out) = AB + B $C_{in}$ = AB + (A+B) $C_{in}$

📍 병렬 가산기

전가산기를 연결해서 구현
단점: 많은 전가산기를 연결함으로써 회로 지연 발생

4.2.2 비교기

📍 1비트 비교기

두 비트를 비교해서 크다, 같다, 작다를 출력하는 회로
LT: less than (A < B)
EQ: equal (A = B)
GT: greater than (A > B)

진가표 (A,B 입력 / LT, EQ, GT 출력)

A	B	LT	EQ	GT	비고
0	0	0	1	0	0=0
0	1	1	0	0	0<1
1	0	0	0	1	1>0
1	1	0	1	0	1=1

논리회로도

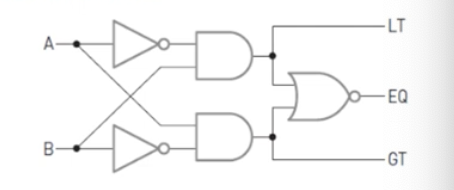
논리식

LT = A'B // A=0, B=1
GT = AB' // A=1, B=0
EQ = A'B' + AB = (LT + GT)'

📍 4비트 비교기

두개의 4비트 2진수를 비교해서 크다(GT), 같다(EQ), 작다(LT) 출력
A = 1010, B = 1001
➡️ LT = 0, EQ = 0, GT = 1

4.2.3 패리티 성생기와 패리티 검사기

📍 패리티 비트(Parity bit)

2진 데이터에 포함된 1의 수를 짝수(또는 홀수)로 맞추도록 추가하는 비트
가장 간단한 오류 검출 방법: 홀수 비트 오류 검출, 오류 수정 불가
통신: 송신부에서 패리티 생성, 수신부에서 패리티 검사

📍 아스키코드에 패리티를 추가한 예

아스키코드	7비트 코드	짝수 패리티	홀수 패리티
'A'	100_0001	0_100_0001	1_001_0011
'T'	101_0100	1_101_0100	0_101_0100

짝수 패리티 문자 'A'가 전송됐다면 수신 데이터가 올바른가?
1) 수신 데이터 0_100_0001? ⭕️
2) 수신 데이터 0_100_1001? ❌ (1의 개수가 홀수. 물론 어느 게 잘못된 건지 정확히는 알 수 없음)
3) 수신 데이터 0_100_1001? ⭕️ (사실은 잘못된 건 맞는데 패리티 검사기는 홀수 개 비트 틀린 케이스만 검출 가능)

📍 XOR 게이트

XOR: 홀수 함수. 1의 수가 홀수일 때 1 출력
입력의 1의 수 + 출력의 1의 수 = 짝수
= 짝수 패리티 생성에 활용 가능

📍 짝수 패리티 생성기(generator)

데이터에 1이 홀수개면 1을 추가
P = X6 + X5 + X4 + X3 + X2 + X1 + X0
XOR 게이트 활용

📍 짝수 패리티 검사기(checker)

데이터에 1이 홀수개면 출력 1, 즉 오류 검출
C = P + X6 + X5 + X4 + X3 + X2 + X1 + X0
XOR 게이트 활용

4.3 조합 논리회로 빌딩블록

학습 목표

자주 사용되는 조합 논리회로 빌딩블록의 동작 이해

내용

4.3.1 인코더와 디코더
4.3.2 멀티플렉서와 디멀티플렉서

4.3.1 인코더와 디코더

인코더: 집합의 원소가 4개일 때 이 4개에 대해 숫자 코드를 만들어내는 것
디코더: 코드를 다시 원래의 4개 원소로 풀어내는 것

📍 인코더

집합의 원소(n개)에 대한 코드( $log_2n$ 비트) 생성

4비트 인코더

입력의 모든 조합을 포함하지 않는다.
입력 신호 중 반드시 1이 하나만 있는 제한적인

우선순위 인코더

입력 신호에 우선순위 부여
4비트 우선순위 인코더(X 입력 / Y, V 출력)

X3	X2	X1	X0	Y1	Y0	V
0	0	0	0	x	x	0
0	0	0	1	0	0	1
0	0	1	x	0	1	1
0	1	x	x	1	0	1
1	x	x	x	1	1	1

X3이 우선순위가 가장 높아서 X3이 1이면 나머지 값과 상관 없이 무조건 3 출력
V: 0000과 0001을 구분하기 위해 추가하는 비트
0000 입력 시 Y1, Y0는 don't care condition. V = 0
우선순위 인코더의 출력
1) X = 0110 ➡️ Y=10, V=1
2) X = 0000 ➡️ Y=xx, V=0
3) X = 0001 ➡️ Y=00, V=0

📍 디코더(decoder)

n비트 코드에 대한 $2^n$ 비트 2진수(one-hot) 출력
One-hot: 비트 중 하나만 값이 다른 2진수

인에이블 제어선이 있는 디코더 (부논리 출력)

E	X1	X0	/Y3	/Y2	/Y1	/Y0
0	x	x	1	1	1	1
1	0	0	1	1	1	0
1	0	1	1	1	0	1
1	1	0	1	0	1	1
1	1	1	0	1	1	1

Enable이 0이면 항상 1 (부논리)
나머지는 부논리이기 때문에 0이 대각선으로 출력
1) E=0, X=01 ➡️ Y=1111
2) E=1, X=01 ➡️ Y=1101
3) E=1, X=11 ➡️ Y=0111

4.3.2 멀티플렉서/디멀티플렉서

📍 멀티플렉서(multiplexer)

여러 개의 입력선 중에서 하나를 선택해서 출력으로 전달
입력 $2^n$ (스위치 선택선 n) ➡️ 출력 1

📍 디멀티플렉서(demultiplexer)

하나의 입력선을 여러 개의 출력선 중 하나로 전달
입력 1 (스위치 선택선 n) ➡️ 출력 $2^n$

📍 2X1 멀티플렉서 구현

S	Y
0	X0
1	X1

Y = S'X0 + SX1

📍 디멀티플렉서

디멀티플렉서 = 인에이블이 있는 디코더
인에이블 제어선이 있는 디코더(출력 정논리)

E	X1	X0	Y3	Y2	Y1	Y0
0	x	x	0	0	0	0
1	0	0	0	0	0	1
1	0	1	0	0	1	0
1	1	0	0	1	0	0
1	1	0	1	0	0	0

디멀티플렉서
: 위의 회로에서 제어선은 신호선으로, 신호선은 선택선으로 변환

S1	S0	Z3	Z2	Z1	Z0
0	0	0	0	0	Y
0	1	0	0	Y	0
1	0	0	Y	0	0
1	0	Y	0	0	0

선택선이 0이면 0이니 신호선으로 들어간 E가 Z0에서 1으로 출력
선택선이 10(2)이면 신호선에서 Z2로 출력

기록+기록

이전 포스트

컴퓨터구조 3강 - 논리회로 기초

다음 포스트

컴퓨터구조 5강 - 순차논리소자

0개의 댓글