학습 목표
- 부울대수: 논리회로에 대한 수학적 배경과 논리연산 규칙을 이해한다.
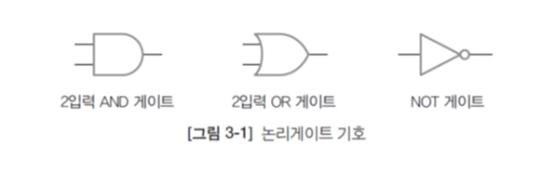
- 논리게이트(logic gate)의 종류와 동작을 이해한다.
내용
- 3.1 논리: 논리 정의, 기본 논리연산 (AND, OR, NOT)
- 3.2 논리 연산 규칙: 부울 대수, 논리식 간소화
- 3.3 논리 게이트: 정논리/부논리, 논리게이트의 종류와 특성
3.1 논리
📍 논리
- 참과 거짓을 다루는 학문
📍 논리 상수
- 논리상수 = (false, true) = (0, 1)
📍 논리 변수
- 문자열로 표시. 예) x, y, z, a1 등
- 입력변수 (입력 신호)
- 출력변수 (출력 신호)
📍 논리 연산
- 입력변수와 출력변수의 관계
📍 논리연산의 표현
- 논리연산 표현 = (논리식, 진가표, 논리회로도)
- 진가표(truth table): 입력과 출력의 결과를 적은 것. 가장 기본
입력변수 목록 - 입력변수 값의 조합
출력변수 목록 - 해당 조합에 대한 출력값 - 예) 짝수 패리티 진가표
x, y, z: 입력변수 목록
F: 출력변수 목록
| x | y | z | F |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
📍 기본 논리 연산
- 논리곱(AND): Z = X*Y = XY = X AND Y
- 논리합(OR): Z = X+Y = X OR Y
- 논리부정(NOT): Z = X'
3.2 논리 연산 규칙
3.2.1 부울대수
📍 대수
- 일련의 공리(axioms - 증명할 필요가 없는 명제)를 만족하는 수학적 구조
- 원소의 집합(set of elements) & 연산자(operator)의 관계
📍 연산자
- 이항 연산자(binary operator)
실수 연산: ➕, ➖, ✖️, ➗
논리 연산: AND, OR - 단항 연산자(unary operator)
실수 연산: 음수, 제곱근, 로그
논리 연산: NOT
📍 부울 대수
- 부울(George Boole, 1815-1864)이 논리값에 적용하는 대수 창안
- 원소의 집합 = {0, 1}
- 연산자 = {AND(*), OR(+), NOT(')}
📍 쌍대식 (dual equation)
- 논리식에 대해 (0 ↔️ 1, AND ↔️ OR)로 교체해서 만든 논리식
- 쌍대식의 정리: 원래의 논리식이 참이면 쌍대식도 항상 참이다.
x*0 = 0 ↔️ x+1 = 1
📍 부울대수 정리
- 닫힘(closure)
- 연산한 결과값이 다시 그 집합의 원소(0, 1)에 속함
- 부울대수는 AND, OR, NOT 연산에 대해 닫혀 있다.
- 결합법칙(associative law)
- (x*y)*z = x*(y*z) for all x, y, z ∈ S
- *와 + 연산에 대해 결합법칙 성립
(x*y)*z = x*(y*z)
(x+y)+z = x+(y+z)
- 교환법칙(commutative law)
- x*y = y*x for all x, y ∈ S
- *와 + 연산에 대해 교환법칙 성립
(x*y) = (y*x)
(x+y) = (y+x)
- 분배법칙(distributive law)
- x*(y*z) = (x*y)*(x*z)
- (*,+), (+,*) 연산에 대해 분배법칙 성립
x*(y+z) = (x*y)+(x*z)
x+(y*z) = (x+y)*(x+z)
- 항등원(identity element)
- e*x = x*e = x for every x ∈ S
- *에 대한 항등원은 1, +에 대한 항등원은 0
x*1 = x
x+0 = x
- 역원(inverse) 또는 보수(complement)
- x*y = e
- 논리변수 x에 대한 역원(보수)는 x'
x*x' = 0
x+x' = 1
📍 드모르간의 법칙(De Morgan's law)
- (x + y)' = x' * y'
- (x * y)' = x' + y'
- (++...+)' = '*'*...*'
- (**...*)' = '+'+...+'
3.2.2 논리식의 간소화
📍 간소화
- 더 간단한 논리회로로 구현 (논리게이트 수 감소)
- x + x * y = x
- x * (x + y) = x
- x + x' * y = x + y
- x * (x' + y) = x * y
- 1-2번째 예, 3-4번째 예는 서로 쌍대식
📍 간소화 원리
- 인접항(adjacent terms)을 찾아 하나로 합침
- 인접항: 논리식에 포함된 AND항(OR항) 중에서 논리 변수 하나의 표현이 다른 항
- 예제 1) x*y의 인접항: x'*y, x*y' (변수 개수만큼 인접항이 있다.)
- 예제 2) (x+y)의 인접항: (x'+y), (x+y')
- 예제 3) x*y*z'의 인접항: x'*y*z', x*y'*z', x*y*z
- 카르노 맵: 인접항을 인접한 곳에 배치해서 간소화하는 방법
3.3 논리게이트
학습 목표
- 논리게이트의 여러 동작 표현에 쓰이는 관례(convention) 이해
- 여러 가지 논리게이트에 대한 기호와 동작 이해
3.3.1 기본 논리게이트
- 논리게이트: 신호가 통과하는 문
📍 전파 지연(propagation delay)
- 입력 신호에 따라 출력신호가 변하는 시간 간격
- 신호가 게이트를 통과하는 시간
- 게이트 통과 때마다 누적
- 일반적으로 수 나노초
📍 전원 공급과 팬아웃
- 원래 트랜지스터로 실제 회로를 만들면 입력신호를 기반으로 전원을 통해 출력을 만들어냄 👉 지연 발생
- 팬아웃: 출력이 실제로는 여러 갈래로 갈라지다보면 전력이 약해져서 실제로는 게이트가 입력값을 제대로 인식하지 못하게 됨. 그래서 실제로는 최대 연결 가능 게이트 수를 8개로 제한
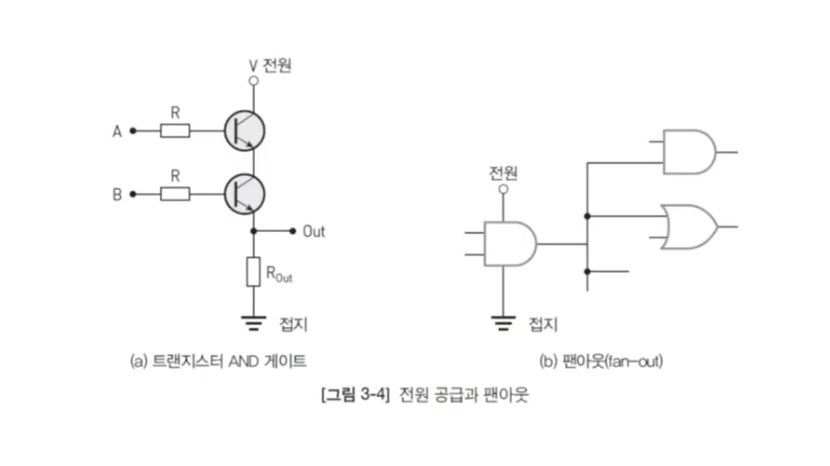
전파지연, 전원 공급, 팬아웃은 논리회로 단계에서는 무시
3.3.2 정논리와 부논리
📍 정논리
- 평상시 상태 0
- 사건 발생 1 (alarm)
📍 부논리
-
평상시 상태 1
-
사건 발생 0
-
신호 이름에 '/' 또는 '-' (/alarm)
-
가능한 정논리/부논리 조합
| 정논리 | 부논리 | |
|---|---|---|
| 입력 | 입력 정논리-출력 정논리 | 입력 정논리-출력 부논리 |
| 출력 | 입력 부논리-출력 정논리 | 입력 부논리-출력 부논리 |
3.3.3 논리게이트 기호
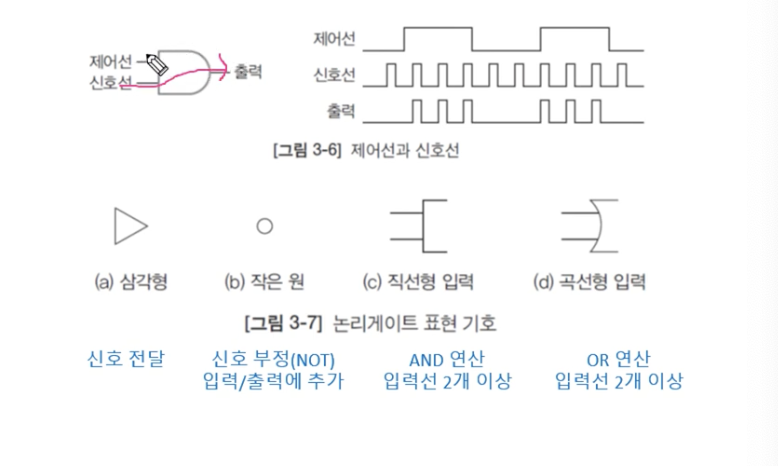
- AND 게이트의 경우 제어선의 값이 0이면 신호선의 값과 관계 없이 항상 0. 제어선이 1이면 신호선이 1일 때만 출력 1
3.3.4 논리게이트 종류
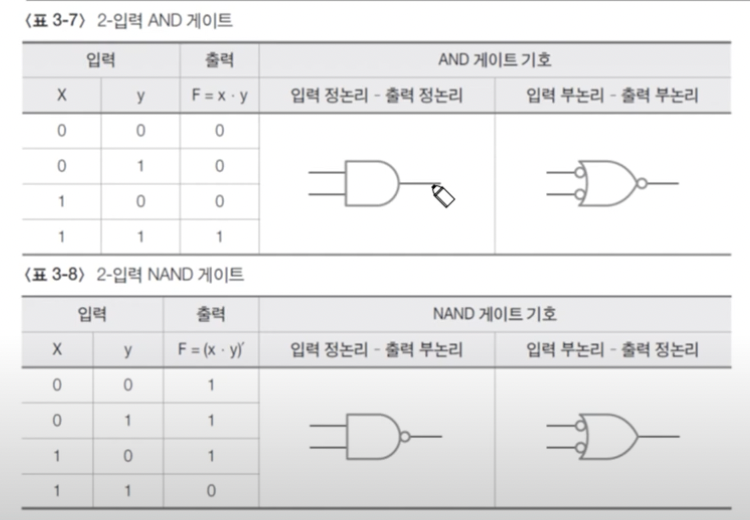
- 표 3-7의 입력 부논리-출력 부논리의 OR: 둘 중 하나가 0이면 0이다로 해석
- NAND: AND NOT 👉 AND의 reverse
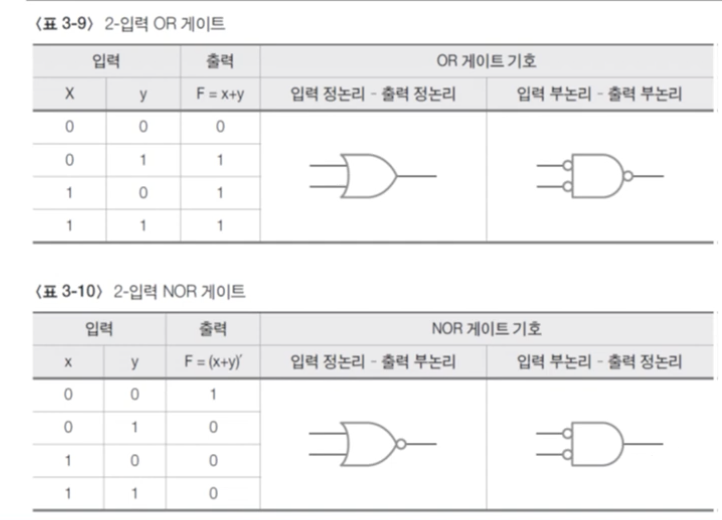
- NOR: OR NOT 👉 OR의 reverse
- 입력 정논리-출력 부논리 조합: 둘 중 하나가 1일 때 0이다.
- 입력 부논리-출력 정논리 조합: 둘 다 0일 때 1이다.
👉 결국 출력값은 같지만 해석의 관점 차이!
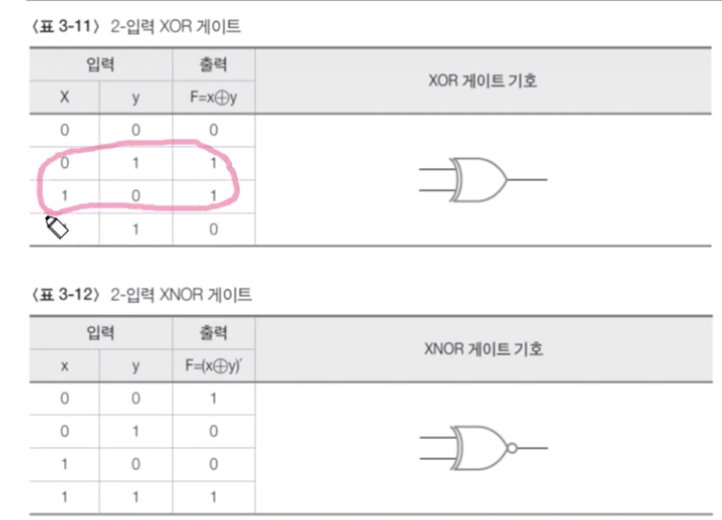
- XOR: 입력 값이 다르면 1, 같으면 0
만일 입력신호 개수가 3개 이상이면 1의 개수가 홀수일 때 1 출력 - XNOR: 입력 값이 같으면 1, 다르면 0
- X는 eXclusive (배타적)
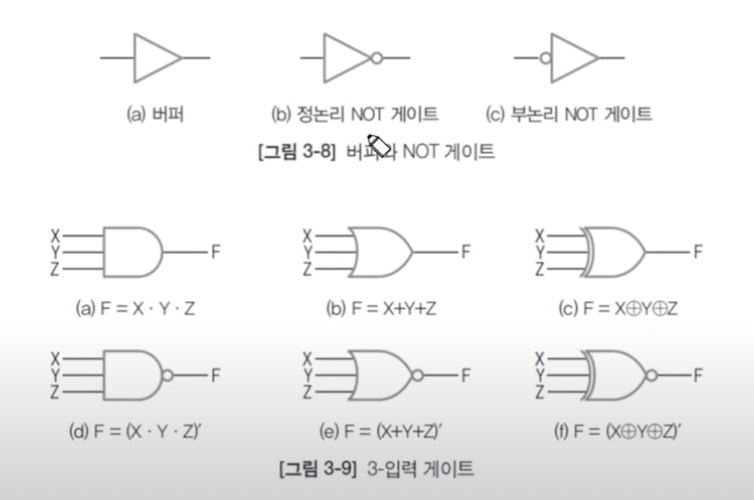
- 입력신호가 1개인 게이트: 버퍼 기준으로 입력에 동그라미가 들어갈 수도(부논리 NOT게이트), 출력에 동그라미가 들어갈 수도(정논리 NOT게이트) 있음
- 버퍼는 약한 신호를 세게 만드는 기능
3.3.5 3상태 버퍼
- 버퍼의 상태가 3가지
Tri-state buffer = {0, 1, Z}
Z = High Impedance (전기가 통하지 못하는 상태 👉 물리적으로 선이 끊어져 있는 상태)
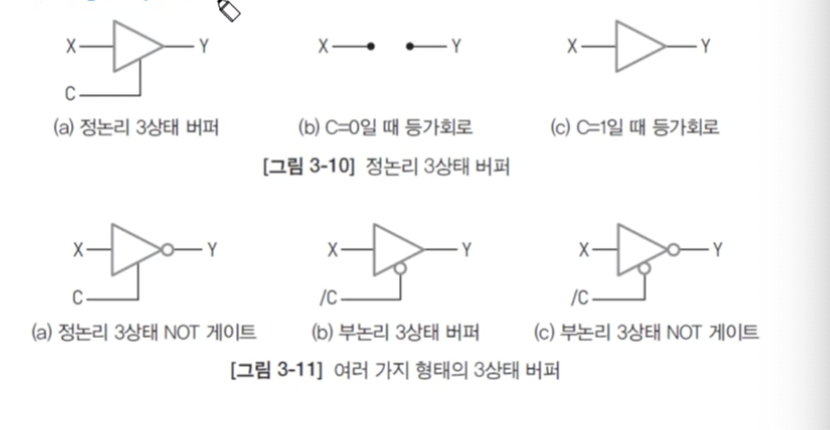
- C: Control
- 정논리 3상태 버퍼
(b) C=0일 때 등가회로: X와 Y가 연결되지 않음
(c) C=1일 때 등가회로: 정상적으로 버퍼를 통해 X와 Y가 그대로 전달이 되도록 연결돼 있음 - 시스템 버퍼 만들 때 사용
