개요
2개의 자연수를 받아 최대공약수를 받기 위해서 2부터 두 자연수 중 작은 자연수까지 모두 나누어보면서 가장 큰 공약수를 구할 수 있다.
일반적으로 사용하는 공통된 소수를 찾아서 최소공배수, 최대공약수를 알아내는 방법으로 알고리즘을 짜면 시간복잡도는 O(n)이지만, 유클리드 호재법을 이용하면 시간복잡도를 O(logN)으로 줄일 수 있다.
구하는 방법은 다음과 같다.
유크리드 호제법사용하기
유클리드 호제법으로 최대공약수 구하기
유클리드 호제법을 이해하기 위해서는 MOD연산에 대해 알아야한다.
MOD연산 : 두 값을 나눈 나머지를 구하는 연산
우선 큰 수를 작은 수로 나눈 나머지를 구한다. (MOD 연산)
1112 mod 695 = 417그 다음, 나눴던 수와 나머지로 또 MOD연산을 한다.
695 mod 417 = 278이 과정을 계속 반복한다.
417 mod 278 = 139
278 mod 139 = 0나머지가 0이 됐을 때, 마지막 계산에서 나누는 수로 사용된 139가 1112와 695의 최대공약수가 된다.
즉, 유클리드 호제법은 MOD연산을 반복하는 것이다.
유클리드 호제법 이해하기
어떻게 유클리드 호제법으로 최대 공약수(GCD)를 구할 수 있었을까?
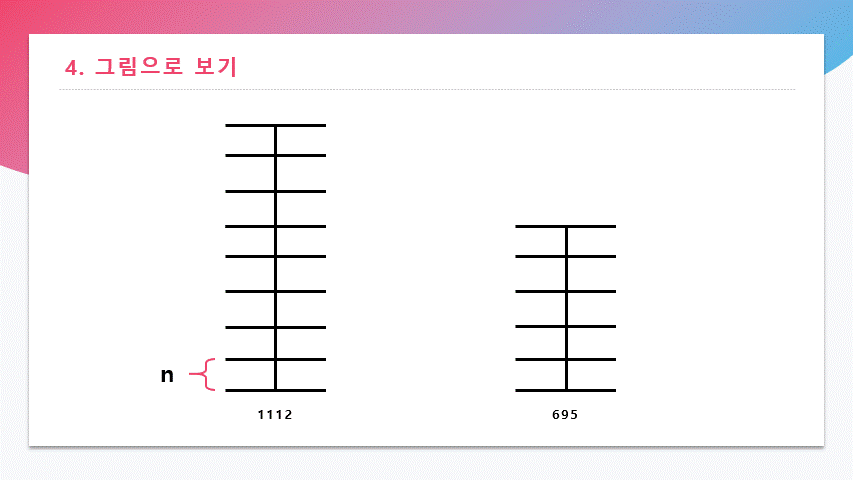
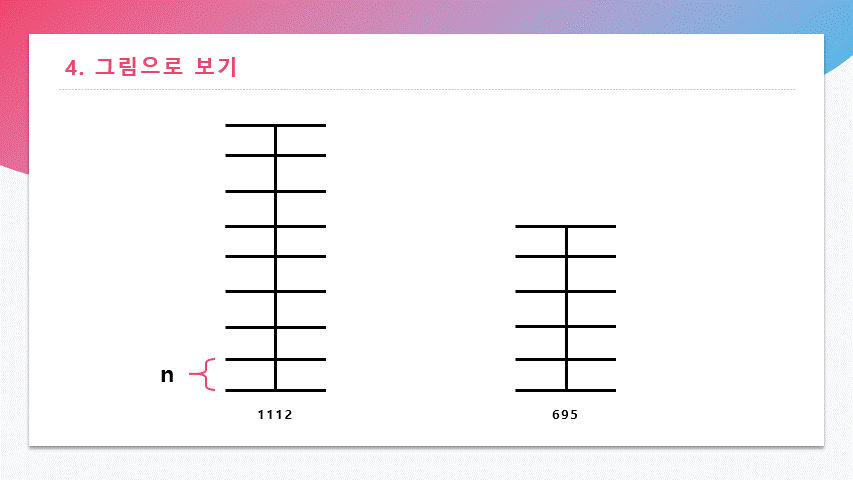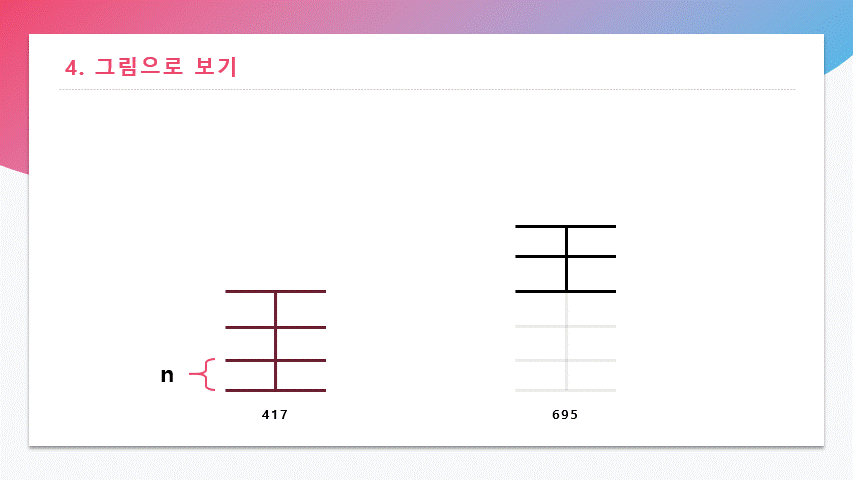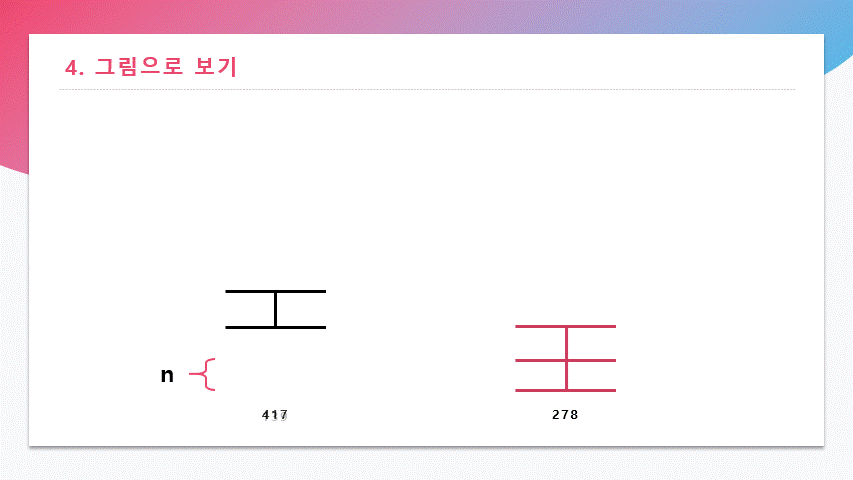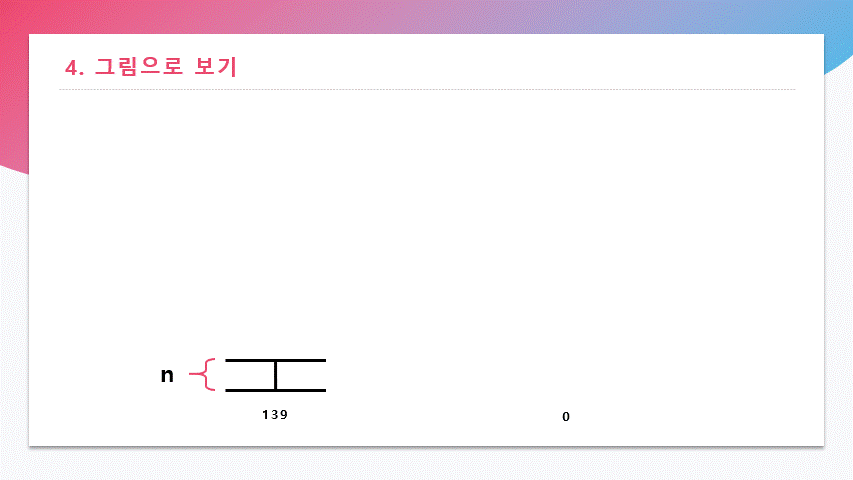
1112와 695를 막대의 기이로 표현한 뒤에, 두 수의 최대공약수 N으로 나눠 보았다.
위에서 우리는 최대공약수가 129라는 것을 알았기 때문에 8칸, 5칸으로 나누었지만 실제로는 모른다고 생각하자,
하지만, 1112와 695가 최대공약수 N의 배수라는 것은 알고 있다.
위에서 한 대로, 1112와 695를 반복해서 MOD 연산을 한다.
이 그림을 통해 연산 중 나온 나머지 417, 278, 139 모두 N의 배수이며 같은 최대공약수를 가진다는 것을 알 수 있다.
278은 139로 나누어 떨어지므로 나머지가 0이고 이때, 최대공약수 N이 139임을 알 수 있다.
관련문제 : 백준 GCD합
출처 : https://velog.io/@yerin4847/W1-%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C-%ED%98%B8%EC%A0%9C%EB%B2%95