백준 11053 / 가장 긴 증가하는 부분 수열

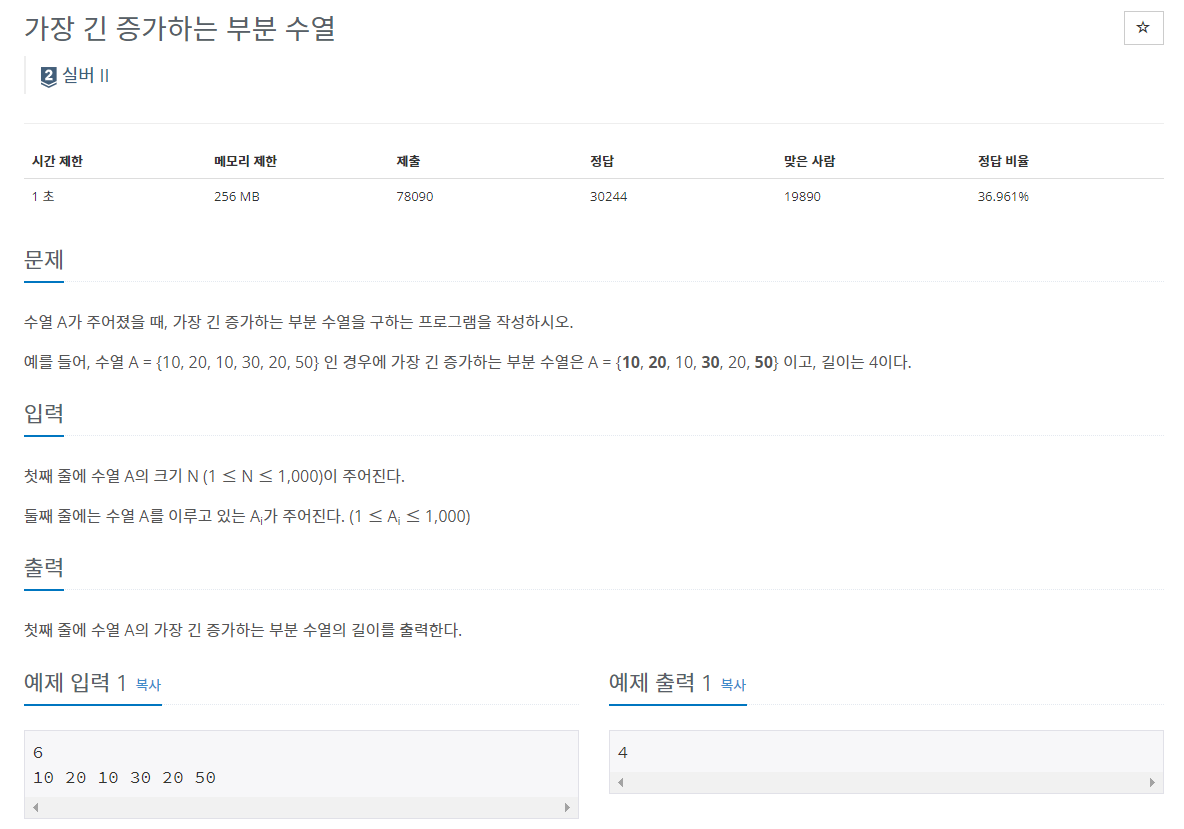
문제

풀이

설명

증가하는 부분 수열 중 가장 긴 것을 구하는 문제이다.

• D[i] = A[1],...,A[i]까지 수열이 있을 때, A[i]을 마지막으로 하는 가장 긴 증가하는 부분 수열의 길이
• 가장 긴 부분 수열이 A[?],A[?],...,A[j],A[i]라고 했을 때, 겹치는 부분 문제를 찾아보자. (A[j]는 A[i] 바로 이전의 수)

D[i] = max(D[j])+1

시간복잡도 : 끝값인 i값과 j값을 반복문으로 비교하기 때문에 O(N^2)의 복잡도를 가진다.

코드

import java.util.Scanner;

public class Num11053 {

	public static void main(String[] args) {
		 Scanner sc = new Scanner(System.in);
		 
	        int n = sc.nextInt();
	        int[] a = new int[n];
	        
	        for (int i=0; i<n; i++) {
	            a[i] = sc.nextInt();
	        }
	        
	        int[] d = new int[n];
	        
	        for (int i=0; i<n; i++) {
	            d[i] = 1;
	            for (int j=0; j<i; j++) {
	                if (a[j] < a[i] && d[i] < d[j]+1) {
	                    d[i] = d[j]+1;
	                }
	            }
	        }
	        
	        int ans = d[0];
	        
	        for (int i=0; i<n; i++) {
	            if (ans < d[i]) {
	                ans = d[i];
	            }
	        }
	        System.out.println(ans);
	}
}

코드설명

참고 :
출처 : https://www.acmicpc.net/problem/11053