0. Array

출처:The Beginner's Guide to JS

연관된 데이터를 사용하기 위한 자료구조 == 순차리스트
JS의 배열은 동적 배열(dynamic array)로 구현되어있어서 배열의 크기를 선언 시점에 고정하지 않고 동적으로 조정

0-1. 배열의 특징

1. 대부분 언어에서 고정된 크기를 가지지만 JS에서는 동적으로 크기가 증감됨
2. 원하는 원소의 Index를 알고 있다면 상수시간(O(1))로 원소 찾음
3. 원소를 삭제하면 해당 index에 빈자리 생김

0-2. 배열 생성

// 1. 빈 Array 생성 
let arr1 = [];

// 2. 미리 초기화된 Array 생성 
let arr2 = [1,2,3,4,5];

// 3. 많은 값 초기화시 fill 사용 
let arr3 = Array(10).fill(0);

//4. 특정 로직으로초기화시 from 사용 
let arr4 = Array.from({length : 10},(_,i)=>I);

0-3. 배열 요소 삭제와 추가

* 배열 요소 삭제

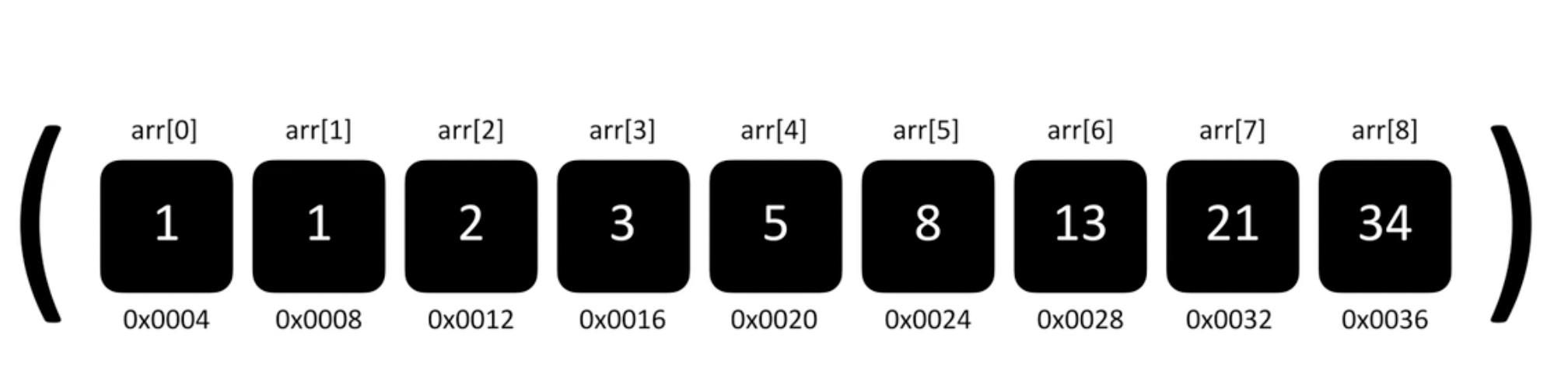
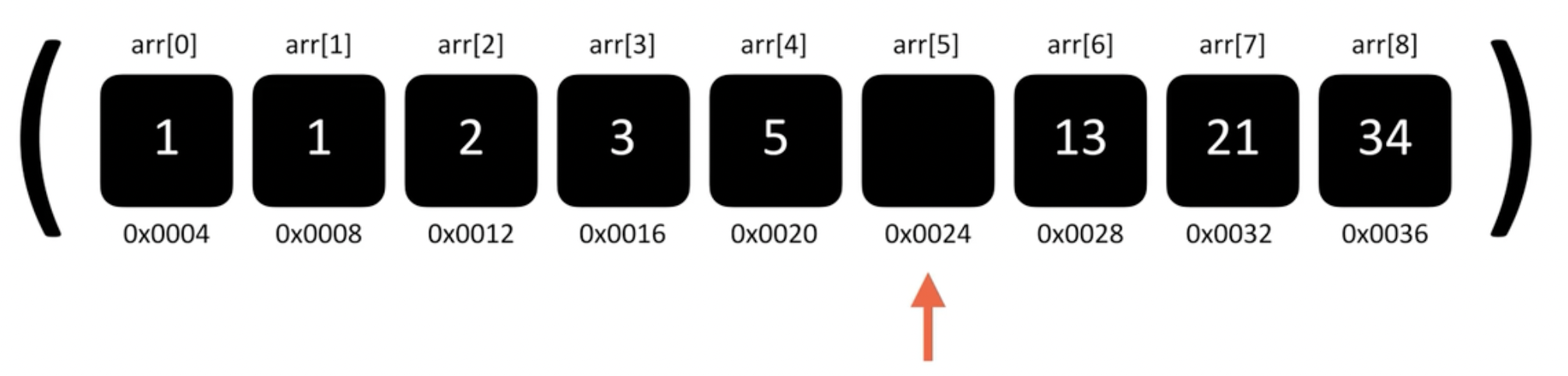
출처:A to Z JavaScript

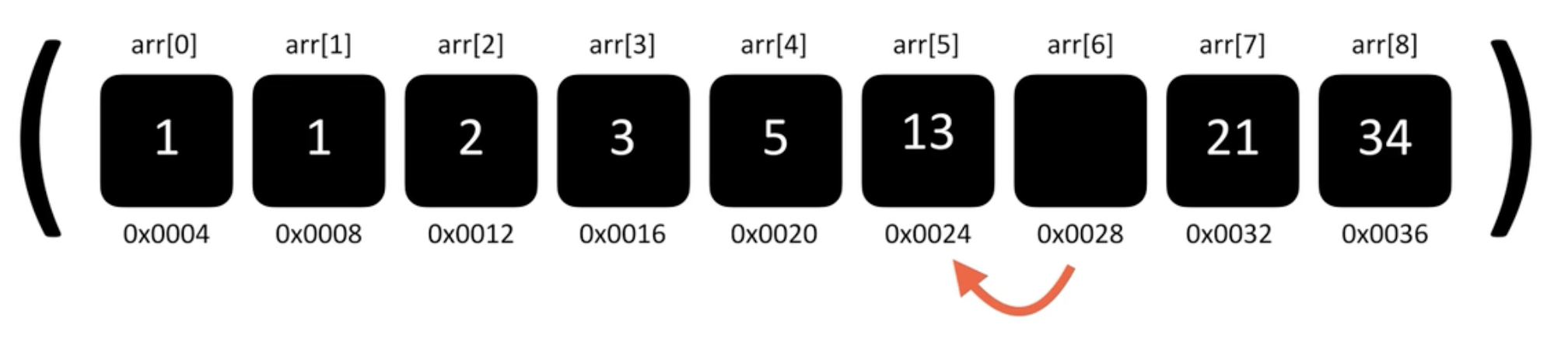
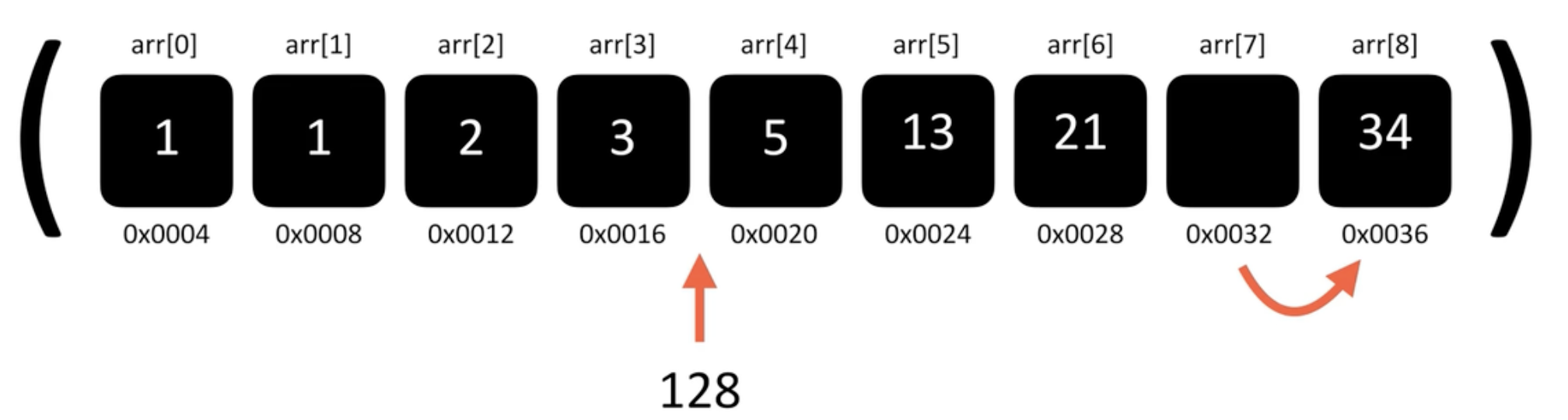
arr[8]의 요소를 arr[7]로 옮기면 배열 요소 삭제 마무리
전체 배열에서 요소 삭제 = 요소 삭제 -> 한 칸씩 앞당김
즉, 배열이 길어질수록(데이터가 증가할수록) 앞 당겨야하는 데이터도 선형적으로 증가하기 때문에 O(n)의 시간복잡도를 가지게됨

* 배열 요소 추가

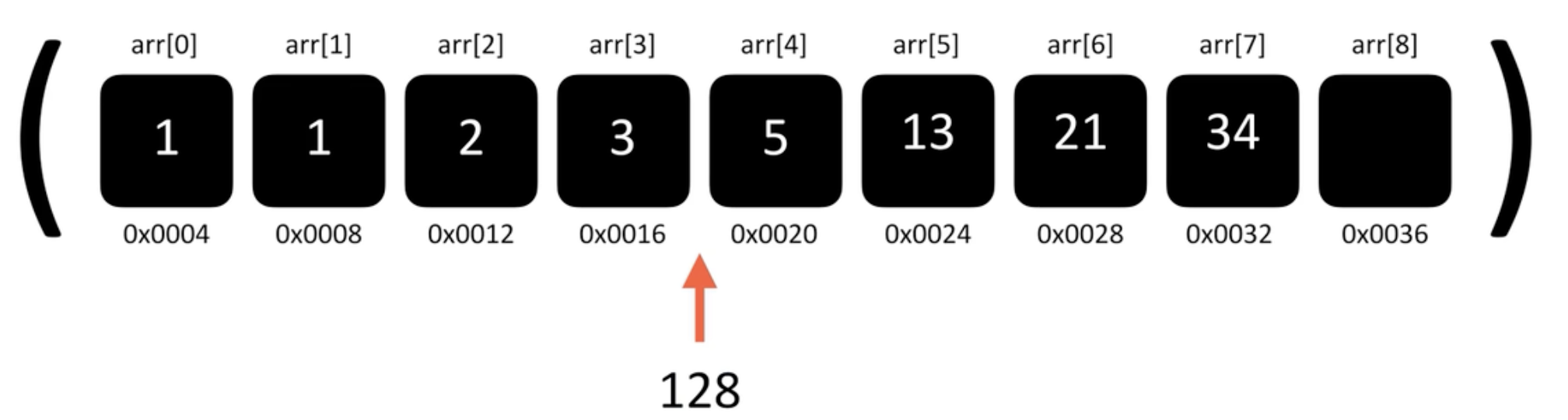
출처:A to Z JavaScript

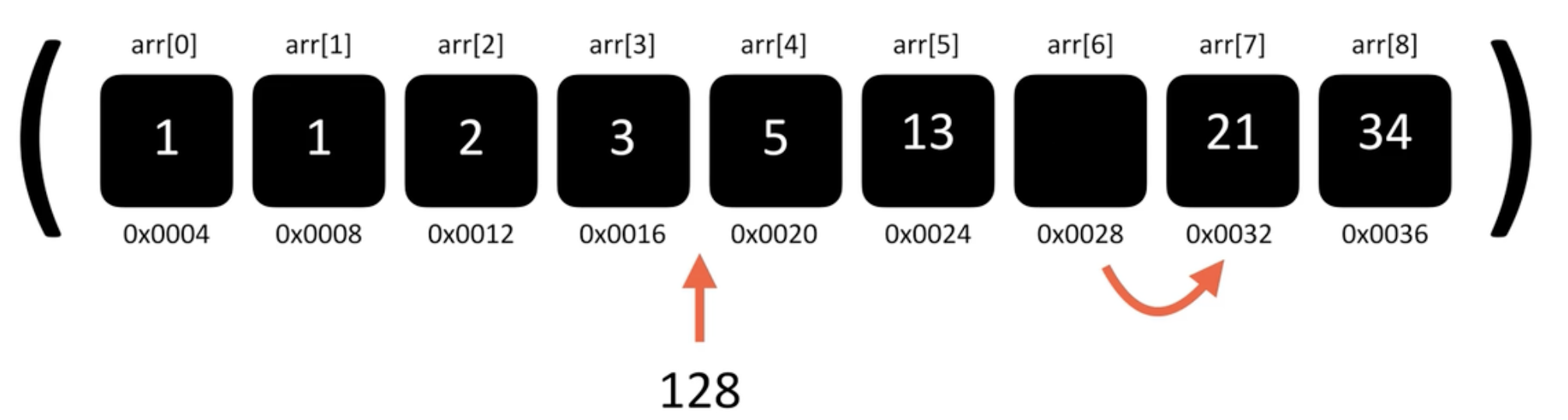
arr[4]에 빈공간이 생겨서 값을 넣으면 배열 요소 추가 마무리
전체 배열에서 요소 추가 = 한칸씩 뒤로 당김 -> 빈 인덱스에 요소 넣기
즉, 배열이 길어질수록(데이터가 증가할수록) 당겨야하는 데이터도 선형적으로 증가하기 때문에 O(n)의 시간복잡도를 가지게됨

Const arr = [1,2,3];

// 4를 배열 끝에 추가
arr.push(4); // O(1)
// push와 pop과 같은 메서드는 배열 요소를 이동시킬 필요가 없기 때문에 O(1)
// 위와 같은 이유로 요소를 이동시키는 shift, unshift는 O(n)

//3번 인덱스에 128 추가
Arr.splice(3,0,128); // O(n)

// 3번 인덱스 삭제
arr.splice(3,1);  // O(n)

결론적으로
배열은 인덱스를 가지고 탐색하는 과정을 거친다면 굉장히 효율적(O(1))이지만
요소를 추가하고 삭제한다면 비효율적일 수 있다(O(n))

+) 배열의 탐색에 대해서 더 정리하자면,
데이터의 특정 위치를 알고 있다면 바로 접근해서 O(1)이 걸리지만, 모른다면 결국 모든 요소를 확인해야하기 때문에 이 경우에도 O(n)이 걸림.

또한 push,pop을 통해 끝 인덱스만을 변형할 경우 O(1)의 복잡도이지만, under the hood의 엔진 동작으로 인해 O(n)을 가짐
-> 예를 들어, 배열의 크기가 매우 크거나 메모리가 많이 사용되고 있는 시스템에서 연속적으로 데이터를 저장할 충분한 공간이 없을때 JS 엔진이 모든 요소를 새로운 위치로 복사 해야함 따라서 배열의 크기에 비례하여 옮기는 데이터의 양도 선형적으로 증가하기 때문에 O(n)이 될 수 있음
-> 이런 경우는 배열의 크기가 매우매우매우 커야한다고 함

하지만 정렬이 되어있거나, 정렬이 가능한 데이터들이라면 이진 탐색같은 알고리즘을 사용해서 배열의 탐색을 O(log(n))까지 줄일 수 있음
따라서 인덱싱을 통한 탐색에는 배열이라는 자료구조가 가장 효율적이라고 표현

• Under the hood란 ?
  : 자동차의 엔진이나 기계장치가 보통 차체 아래(즉, 'hood' 아래)에 숨겨져 있음을 뜻하는 비유에서 유래. 보통 사용자나 프로그래머에게는 보이지 않지만, 시스템이나 소프트웨어가 실제로 어떻게 작동하는지를 설명하는 데 사용되는 표현
  저 설명에서는 push pop이 굉장히 간단한 메서드지만 메모리 할당, 요소의 이동, 가비지 컬렉션 등 많은 복잡한 과정이 뒤 따르는 부분이 있기에 under the hood 엔진 동작이라고 표현

1. Linked List

이전에 배열의 자료구조의 결론에서 요소를 추가하고 삭제하는 작업이 반복적으로 이루어져야 한다면 굉장히 비효율적이라는 것을 확인함

이에 따라서 요소의 추가 삭제 작업에 더 적합한 자료구조가 등장함
그것이 바로 Linked List(연결 리스트)!

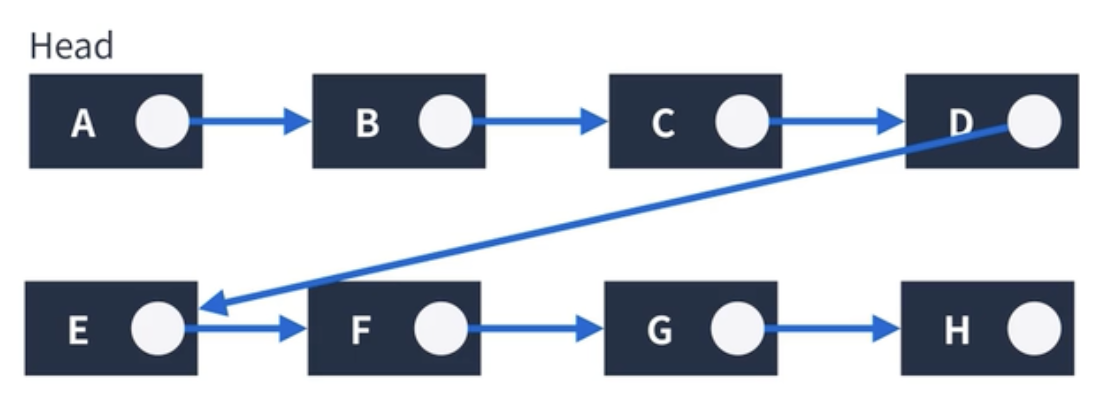
연결 리스트는 각각의 node들로 구성됨
가장 첫번째 node를 Head라고 정의하고, 각 node는 데이터를 가진(위 이미지에서는 영문자) 데이터 영역과 다음 node를 가리키는 포인터 영역으로 구성됨

1-1. Linked List의 특징

1. 메모리가 허용하는 한 요소를 제한없이 추가
2. 탐색은 O(n)이 소요되지만 추가 삭제는 O(1) 소요
3. Singly Linked List와 Doubly Linked List, Circular Linked List 존재

1-2. Array와 차이점

• 배열의 메모리
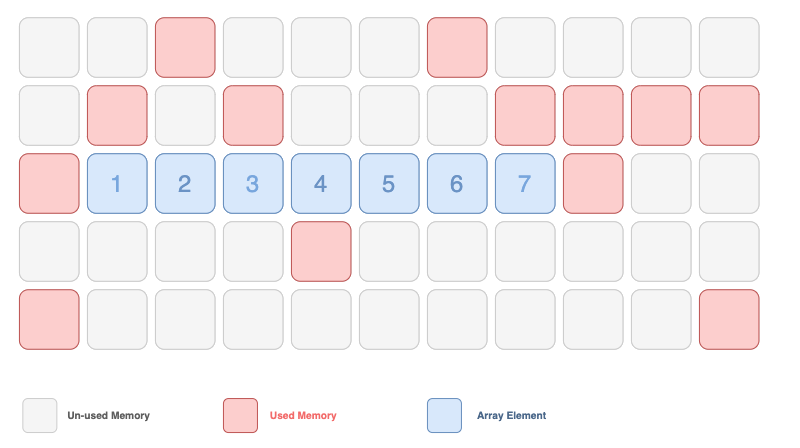  출처: Matthew Chan Medium
  배열의 경우 저장된 요소의 값이 메모리 상에서 연속적으로 위치함
  따라서 조회할때 linked List처럼 연결 노드를 찾아다니지 않아도 됨
  하지만 요소를 추가하거나 삭제할 경우 차지하는 영역의 리사이징(요소 위치 당기던 작업)이 필요함 -> 비효율적

• Linked List의 메모리
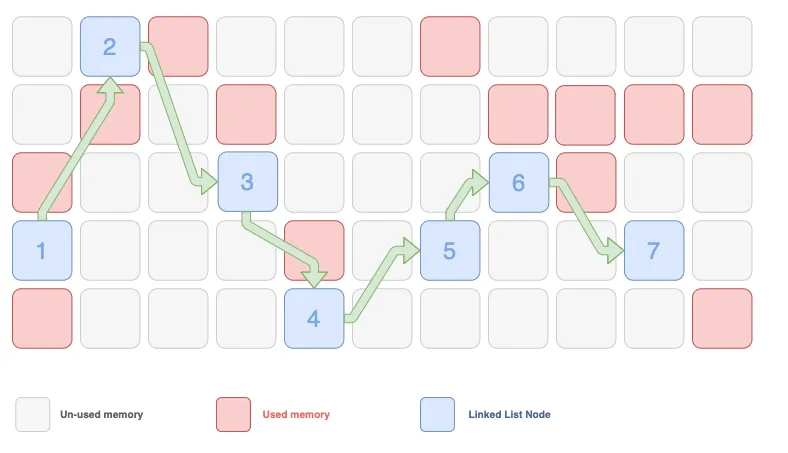  출처: Matthew Chan Medium
  Linked List의 경우, 연속적인 위치가 아닌 다음 노드의 위치를 가지고 추적하기에 요소를 조회할 때 더 많은 연산이 필요함
  하지만 추가와 삭제 시, 리사이징을 거치지 않아도 되기에 효율적임

1-3. Singly Linked List

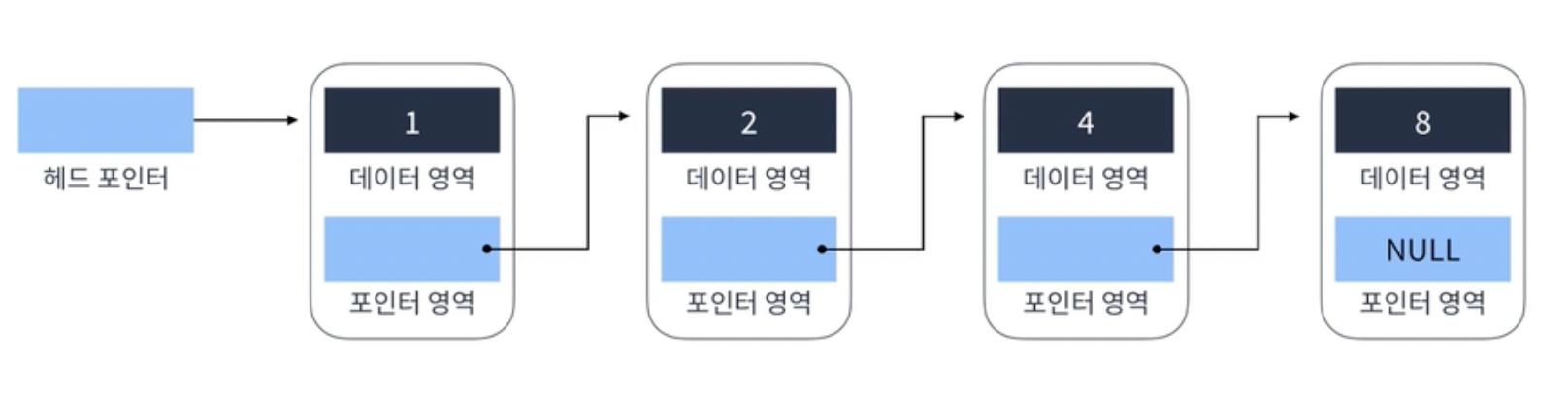
Head에서 Tail까지 단방향으로 이어지는 연결리스트. 가장 단순한 형태
포인터 영역이 Null이면 그 리스트의 가장 마지막 노드 = Tail
Head는 해당 리스트의 가장 첫번째 node
Head Pointer는 Head를 참조하는 포인터

(지피티 왈 : 헤드 포인터는 헤드 노드를 가리키는 포인터이고, 헤드는 리스트의 첫 번째 노드입니다. 이 둘은 조금 다르지만, 실제로는 헤드 포인터를 통해 헤드 노드에 접근하므로 종종 혼용되어 사용됩니다.)

Signly Linked List의 핵심 로직

1. 요소 찾기
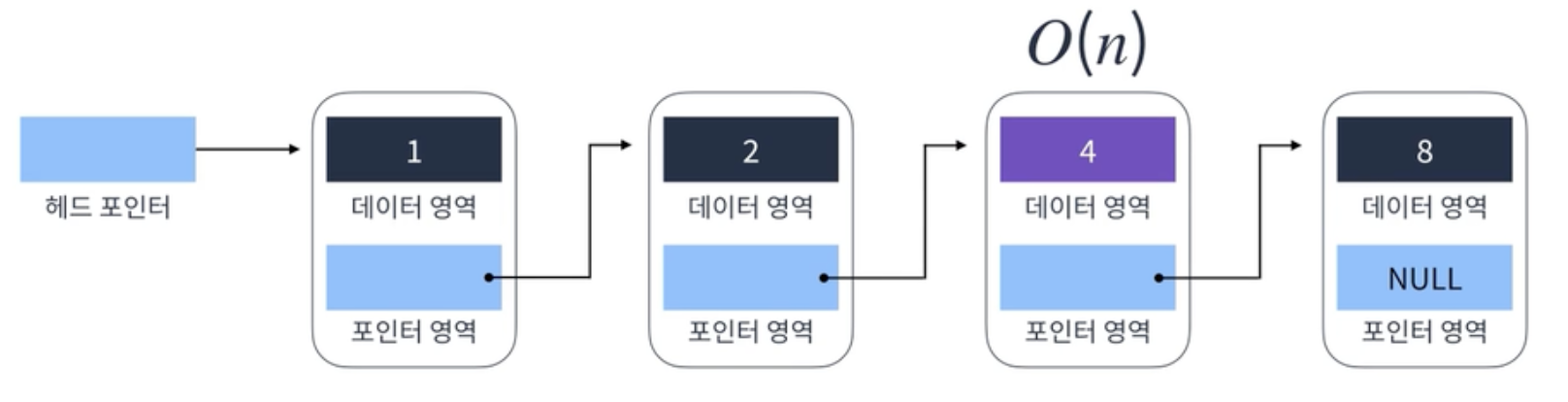1. headPointer가 head 찾음
2. head의 데이터 영역을 살피고 찾는 값이 아니면 포인터 영역 참조해서 next Node로 이동
3. 원하는 데이터 찾을때까지 무한 반복
따라서 배열의 크기가 커질수록(데이터가 증가할수록) 참조해서 비교하는 데이터도 선형적으로 증가함
-> O(n)

2. 요소 추가
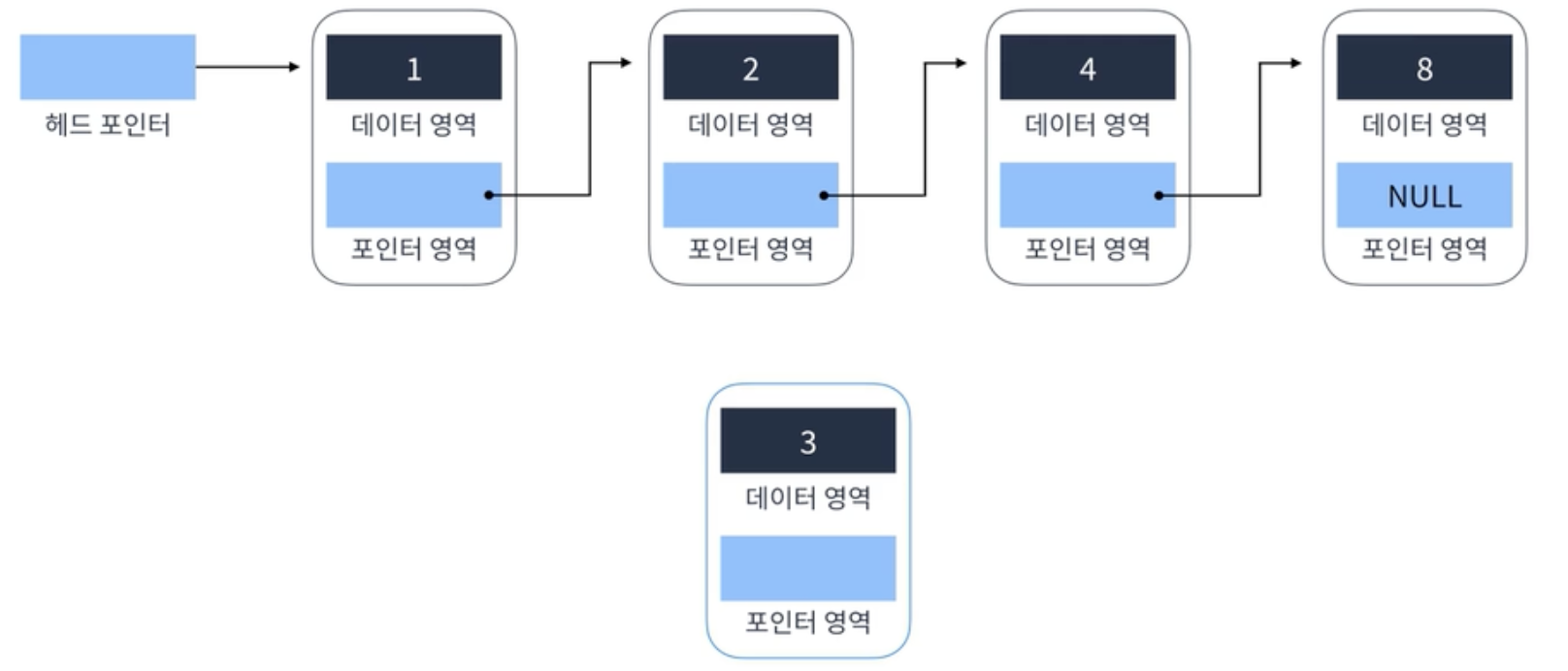
3이라는 데이터를 가진 Node를 2 데이터와 4 데이터 사이에 추가하고 싶음
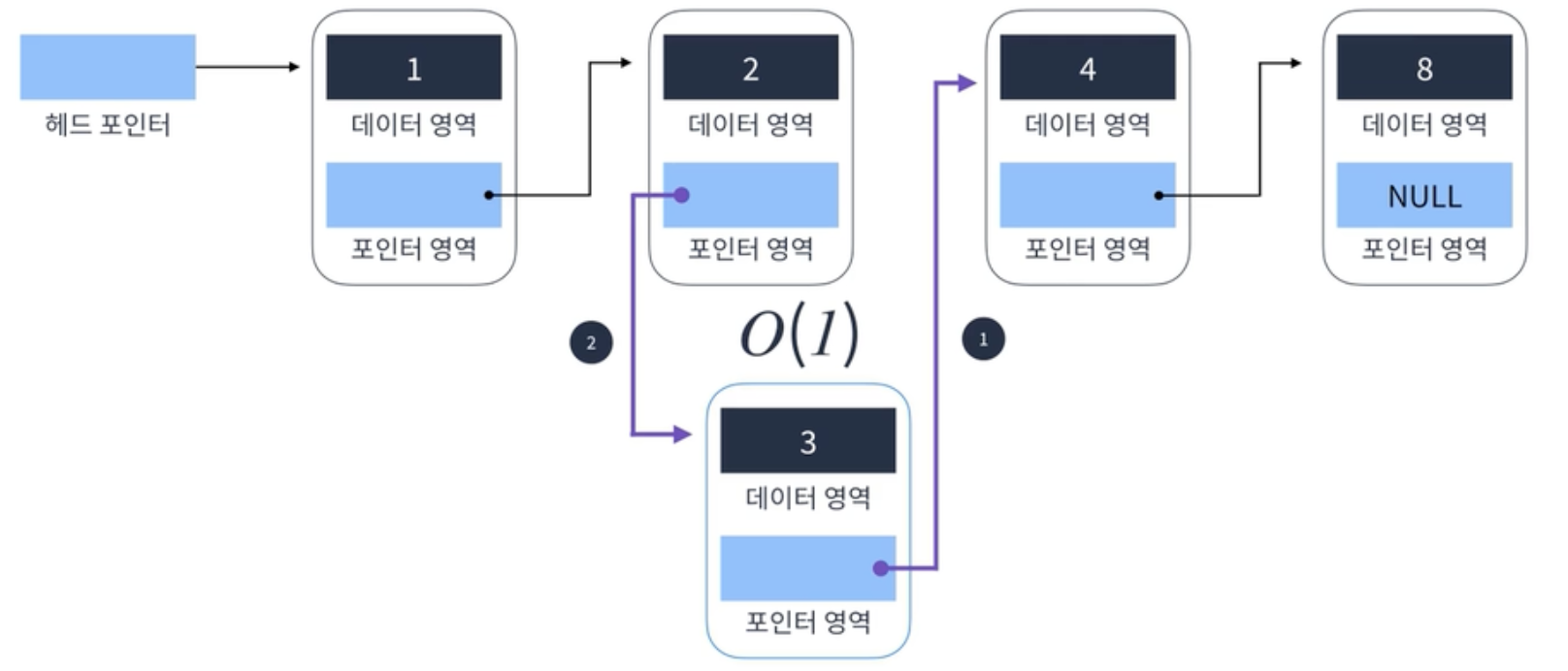1. 추가할 node의 포인터가 4 데이터를 가리키게 함
2. 2 데이터를 가진 node의 포인터가 추가할 node를 가리키게함
-> O(1)

(하지만 2를 가진 데이터를 탐색하거나 4를 가진 데이터를 탐색한다면 다시 선형시간 소요. 따라서, 추가를 위한 탐색을 하지 않도록 주의하며 코드를 작성해야함)

3. 요소 삭제

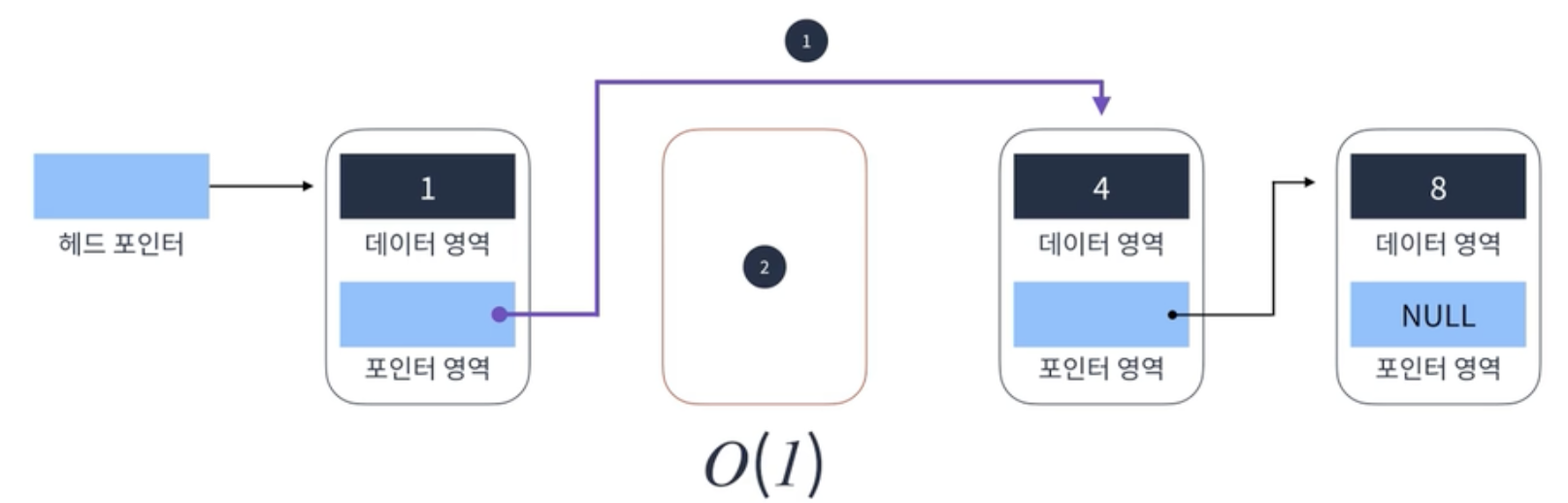
2 데이터를 가진 node를 삭제하려면
1. Prev node가 삭제하려는 node의 next node를 가리키게함
2. 2 데이터를 가진 node 메모리에서 삭제
-> O(1)

1-4. Doubly Linked List

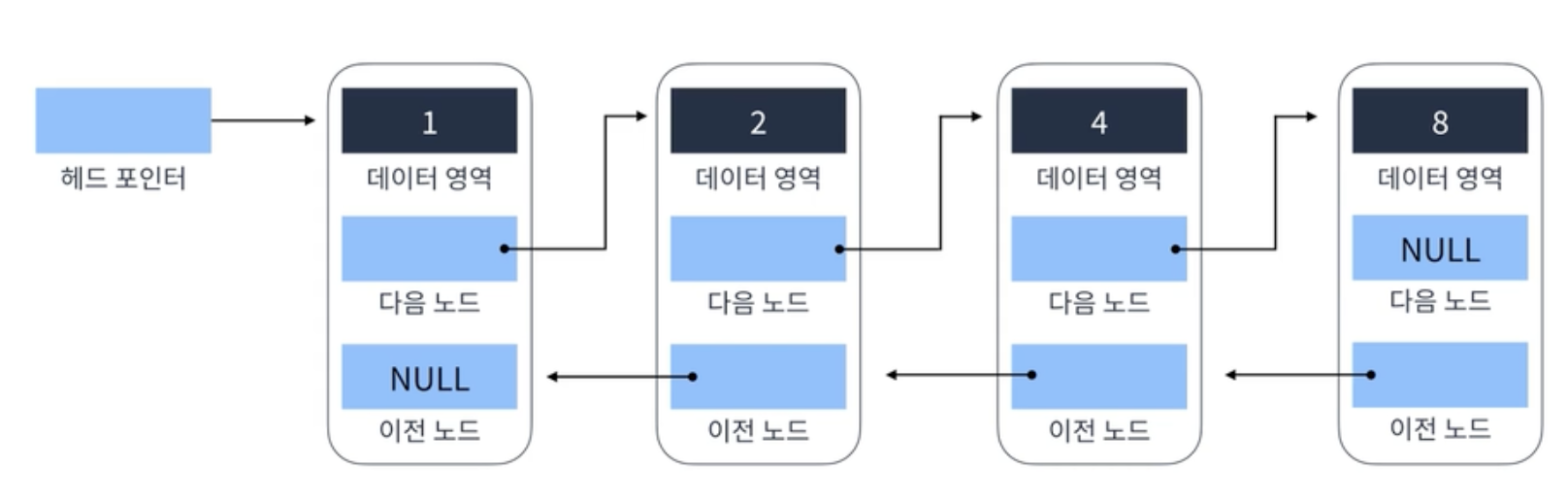
양방향으로 이어지는 연결 리스트 (이중 연결 리스트)
Signly 보다 자료구조의 크기가 더 큼

1. 요소 추가

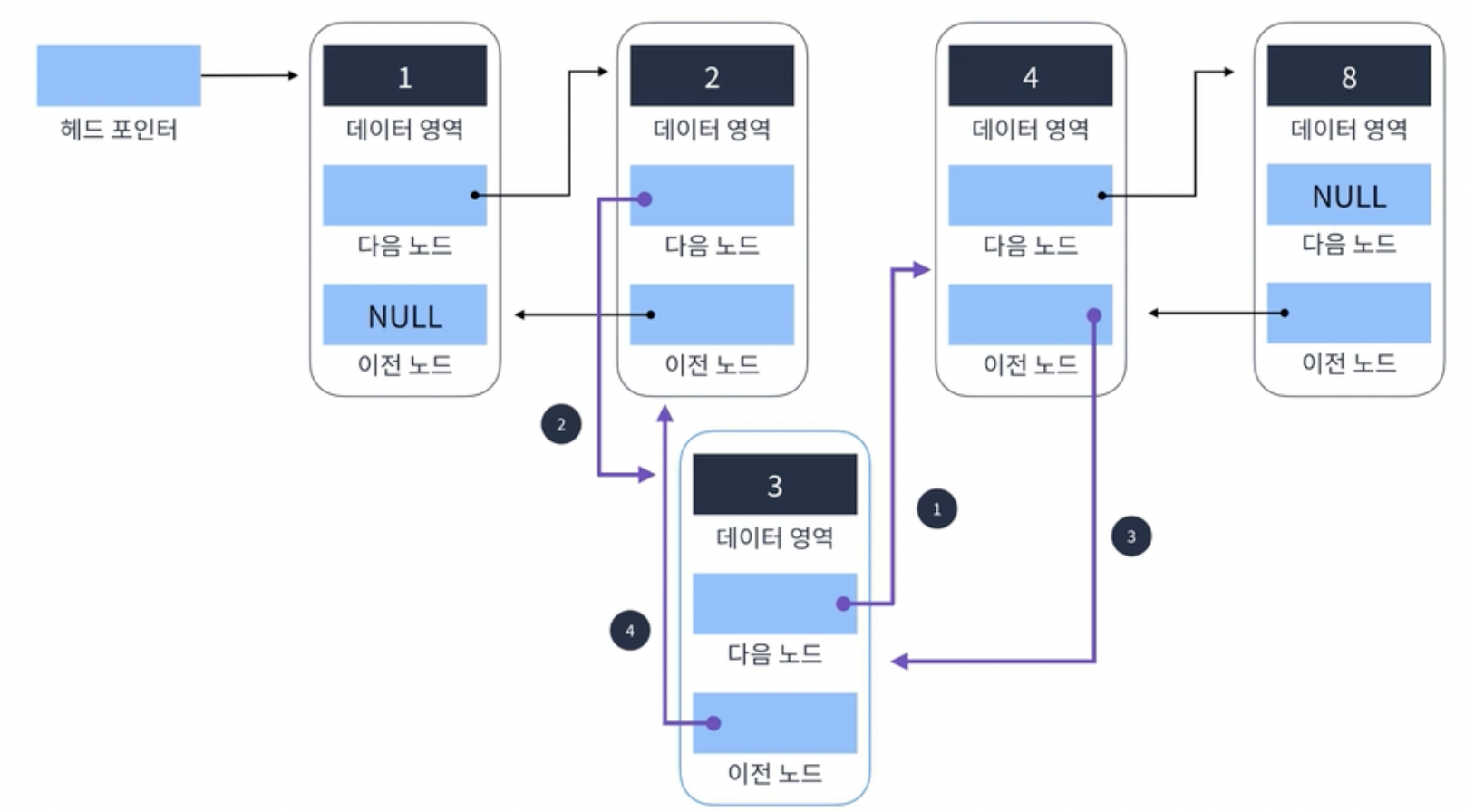
1. 추가할 node의 next node를 4데이터를 가진 node로 가리키게함
2. 2데이터를 가진 node의 next node를 추가할 node로 가리키게함
3. 4데이터를 가진 node의 prev node를 추가할 node로 가리키게함
4. 추가할 node의 prev node를 2데이터를 가진 node로 가리키게함
-> O(1)

2. 요소 삭제

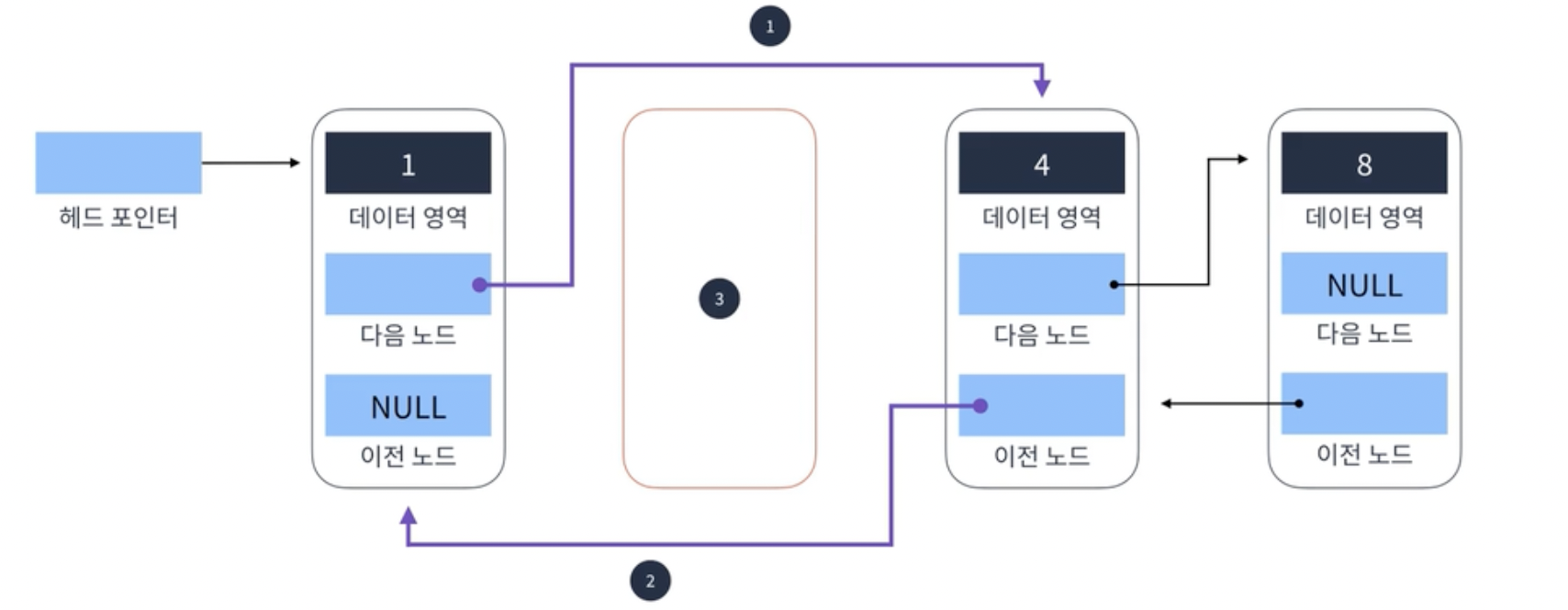
2데이터와 4 데이터 사이의 3데이터를 가진 node 삭제하기
1. 2데이터를 가진 node의 next node를 4데이터를 가진 node로 가리키게함
2.4데이터를 가진 node의 prev node를 2 데이터를 가진 node로 가리키게함
3. 3 데이터 가진 node를 메모리에서 삭제
-> O(1)

1-5.Circular Linked List

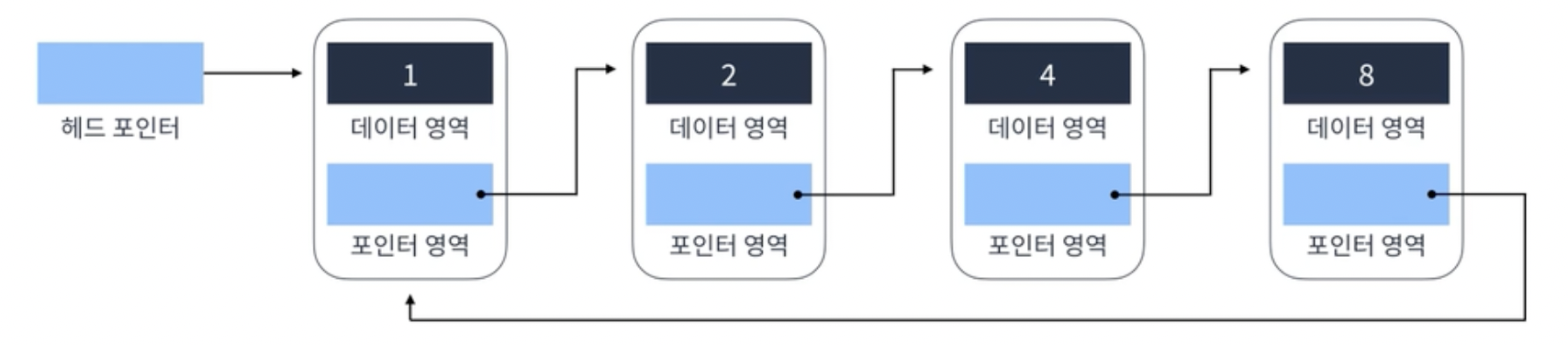
단일 혹은 이중에서 Tail이 Head로 연결되는 리스트
메모리 아껴쓸 수 있음. 원형 큐 만들때도 사용

순회 시간: Circular Linked List는 순회할 때 특정 노드에서 시작하여 마지막 노드에 도달하면 다시 첫 번째 노드로 돌아가는 특성을 가지고 있습니다. 이로 인해 순회 연산이 효율적으로 수행될 수 있습니다. 만약 캐싱 시 데이터를 순회하며 접근해야 하는 경우, Circular Linked List를 사용하면 순회 시간을 줄일 수 있어 캐시 히트(hit) 확률을 높일 수 있음

+) 단일리스트를 코드로 정리

class Node {
	constuctor(value) {
		this.value = value;
		this.next = null;
	}
}

class SinglyLinkedList {
	constructor() {
		this.value = null;
		this.tail = null;
	}
	
	// 요소 찾기
	find(value) {
		let currNode = this.head;
		while (currNode.value !== value) {
			currNode = currNode.next;
		}
		return currNode;
    }


	// 요소 추가하기
	append(newValue) {
		const newNode = new Node(newValue);
		if (this.head === null) {
			this.head = newNode;
          	this.tail = newNode;
		} else {
         	this.tail.next = newNode;
			this.tail = newNode;
		}
	}

	// 요소 중간에 추가하기
	insert(node, newValue) {
		const newNode = new Node(newValue);
		newNode.next = node.next;
		node.next = newNode;
	}


	// 요소 삭제하기
	remove(value) {
		let prevNode = this.head;
		while (prevNode.next.value !== value) {
			prevNode = prevNode.next;
		}
      
		if (prevNode.next !== null) {
			prevNode.next = prevNode.next.next;
        }
}

const linkedList = new SignlyLinkedList();
linkedList.append(1);
linkedList.append(2);
linkedList.append(3);
linkedList.append(5);
console.log(linkedList.find(3)); // Node { value : 3, next : Node { value : 5, next :null } }

	

참고 자료

• Matthew Chan Medium
• JSTutorial
• A to Z JavaScript