자료구조의 종류

사진출처 : A to Z : JavaScript

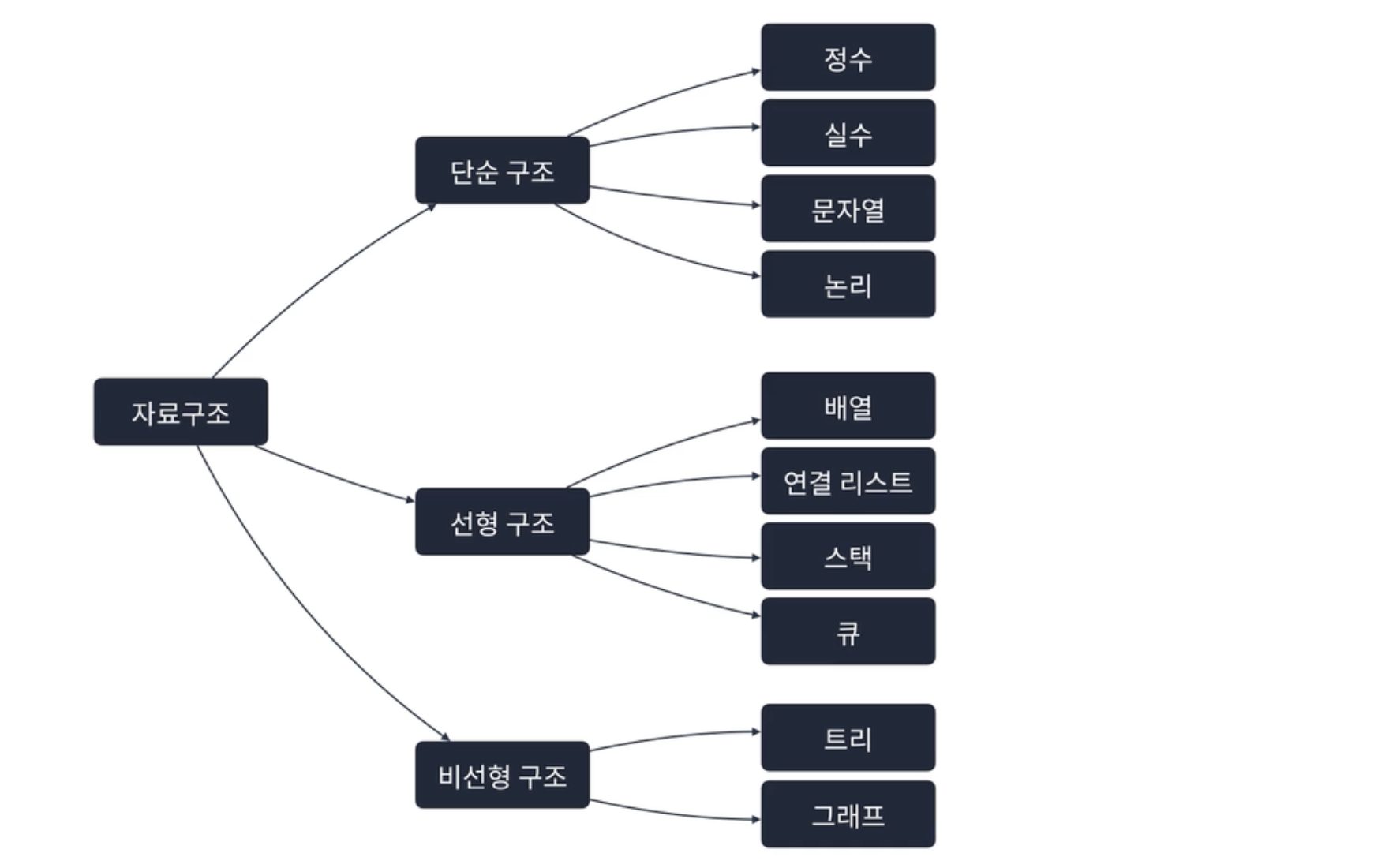
자료구조는 크게 3가지로 분류할 수 있음
단순 구조, 선형 구조, 비선형 구조
그 중에서도 선형과 비선형에 대해 간략하게 정리하겠음

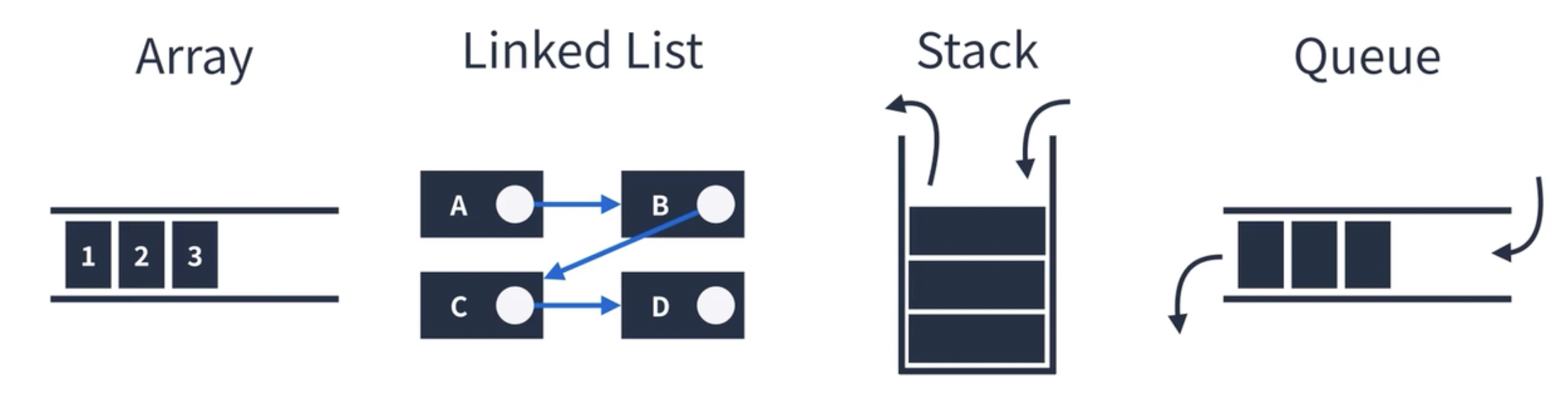
• 선형 구조 : 한 원소 뒤에 반드시 하나의 원소만 존재하는 구조 (자료가 선형으로 존재하는 구조) Array, Linked List, stack, queue 해당
  사진출처 : A to Z : JavaScript

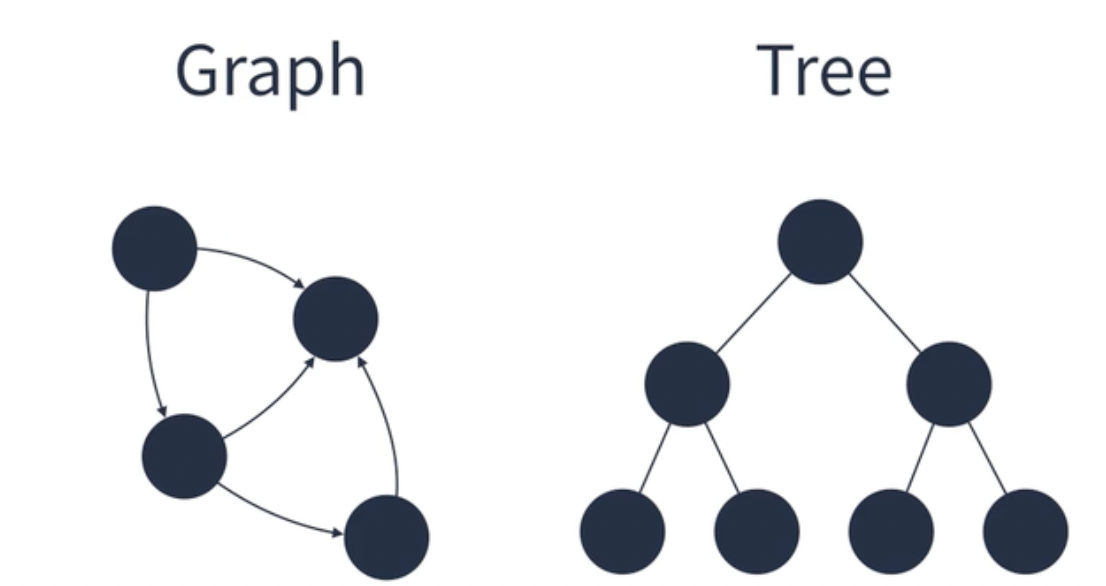
• 비선형 구조 : 원소간 다대다 관계를 가지는 구조 (계층적 혹은 망형 구조) tree, graph 해당
  사진출처 : A to Z : JavaScript

시간 복잡도

프로그램의 성능을 완벽히 비교하려면 하드웨어의 성능부터 운영체제의 성능, 컴파일러 최적화, 입력 크기 등 고려해야 할 부분이 많음
따라서 정확히 성능을 비교하는 것은 불가능하지만 대략적인 성능을 비교하기 위해 Big O 표기법(시간복잡도를 표현하기 위한 방법으로 점근적 표기법 중 하나)을 만들어서 사용함

사진출처 : Carnegie Mellon University

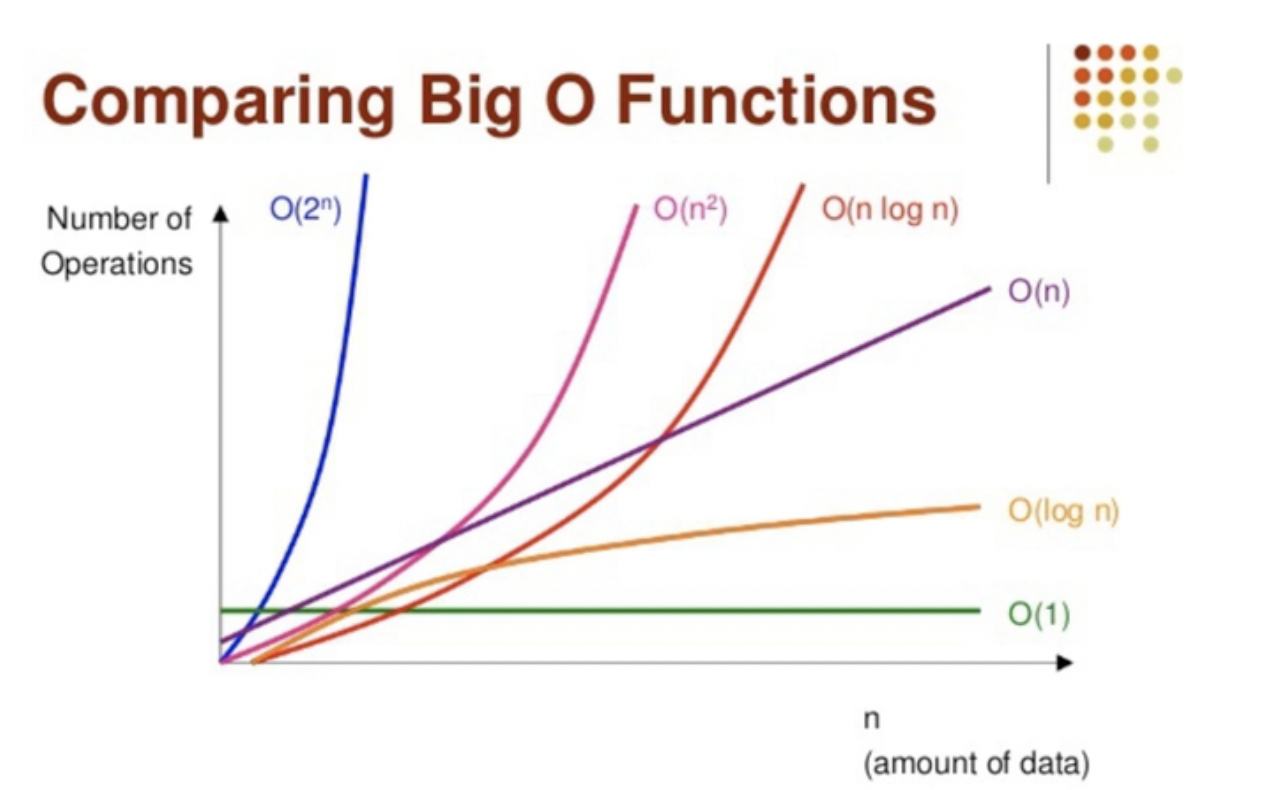
n을 기준으로 입력 데이터의 양에 따라 연산의 수가 얼만큼 증가하는가(=시간 복잡도)를 나타내는거임

O(1) < O(logn) < O(n) < O(nlogn) < On^2 < O2^n

로그시간부터 코드를 정리하면 아래와 같음

// 로그 시간
// O(logn)
for (let i = 0; i <= n; i *= 2) {}


// 선형시간
// O(n)
for (let i = 0; i < n; i += 1) {}


// 선형지수시간
// O(nlogn)
for (let i = 0; i < n; i += 1) {
  for (let j = 0; j <= n; j *= 2) {}
}


// 2차시간
// On^2
for (let i = 0; i < n; i += 1) {
  for (let j = 0; j < n; j += 1) {}
}

위와 같이 for문을 가지고 코드로 정리해볼 수 있음
예시 코드는 없지만 지수시간(O2^n), 팩토리얼 시간(On!)은 코드상으로 가급적 사용하면 안됨

📌 점근적 표기법

알고리즘의 계산 복잡성을 비교한다고 가정했을 때

A 알고리즘 계산 복잡성 : 16πn^2+23n
B 알고리즘 계산 복잡성 : 100000𝑛+10000

어느 것이 더 효율적인 알고리즘인가? -> 예측하기 어려움
예측에 대한 어려움을 해결하기 위해 우리가 알고있는 로그, 지수, 다항함수 등과의 비교로 표현 -> 계산 복잡성의 증가 양상을 단순화시킴
그게 점근적 표기법임
총 다섯가지의 점근적 표기법이 있고, 그 중 big O 표기법을 가장 많이 사용함
이유는 최악의 경우(입력에 대해 가장 나쁜 성능을 보여주는 경우)에도 해당 알고리즘이 어떤 성능을 낼지 가늠해볼 수 있기 때문

그래프를 해석하면, 𝑓(𝑛)이 𝑔(𝑛)에 한 없이 가까워질 수 있지만 그걸 넘을 수는 없음 쉽게 말해서 𝑔(𝑛)은 𝑓(𝑛)의 한계치임 ㅇㅇ
이걸 다른 말로 점근 상한(an asymptotic upper bound)이라함

위 그래프를 만족하는 𝑓(𝑛)를 𝑂(𝑔(𝑛))이라고 표시하는데
내 알고리즘 𝑓(𝑛)이 𝑂(𝑔(𝑛))에 속한다면, 𝑓(𝑛)의 계산복잡도는 최악의 경우라도 𝑔(𝑛)과 같거나 혹은 작게 되는 것을 알 수 있음
따라서 점근적 표기법을 통해 알고리즘의 계산 복잡성의 증가 양상을 단순화시킴으로써 알고리즘의 성능을 대략적으로 비교하는 데 도움을 주게됨~

bigO 4가지 법칙

이러한 점근 상한의 개념이 있기 때문에 bigO에서 4가지 법칙이 있음

1. 계수 법칙
상수 k가 0보다 클 때, 𝑓(𝑛) = 𝑂(𝑔(𝑛))이면 k𝑓(𝑛) = 𝑂(𝑔(𝑛))

// 두 개의 for문 모두 O(n)으로 표기
for (let i = 0; i < n; i++) {}
...
for (let i = 0; i < 5*n; i++) {}

2. 합의 법칙
𝑓(𝑛) = 𝑂(h(𝑛)), 𝑔(𝑛) = 𝑂(p(𝑛))일 때, 𝑓(𝑛)+𝑔(𝑛) = 𝑂(h(𝑛))+𝑂(p(𝑛))

// 두 for문을 합하여 O(n+m)으로 표기
for(let i = 0; i < n; i++) {}
for(let i = 0; i < 6*n; i++) {}

3. 곱의 법칙
𝑓(𝑛) = 𝑂(h(𝑛)), 𝑔(𝑛) = 𝑂(p(𝑛))일 때, 𝑓(𝑛)𝑔(𝑛) = 𝑂(h(𝑛))𝑂(p(𝑛))

// 두 for문을 곱하여 O(n^2)으로 표기
for(let i = 0; i < n; i++) {
	for(let j = 0; j < 2*n; j++) {}
}

4. 다항 법칙
𝑓(𝑛)이 k차 다항식이면, 𝑓(𝑛) = 𝑂(nᵏ)

// O(n^3)으로 표기
for(let i = 0; i < n*n*n; i++) {}

이렇게 big o 표기법의 4가지 법칙에 대해서 알아봄
여기서 기억해야할 핵심은 두 가지
1. 상수항 무시 (계수법칙 참고)
2. 가장 큰 항 외에 무시

for (let i = 0; i < n; i++) {}

for (let i = 0; i < n; i++) {
	for(let j = 0; j < n; j++) {}
}
// 이 코드는 합의 법칙에 의해 O(n^2+n)이지만 작은 항은 무시하여
// O(n^2)라고 표기해도 됨

위의 질문을 다시 한 번 가져와서 물어보면

A 알고리즘 계산 복잡성 : 16πn^2+23n
B 알고리즘 계산 복잡성 : 100000𝑛+10000

이제는 big O 표기법에 따라서 효율성을 예측할 수 있게 됨
A는 n^2이고 B는 n이니까
데이터 수가 증가함에 따라 A 알고리즘의 계산복잡도는 지수적으로, B 알고리즘은 선형적으로 증가하므로 B 알고리즘이 더 효율적이라 판단 가능!

참고 자료

• ratsgo.github
• A to Z JavaScript
• hanamon

빅오 표기법 외에도 빅오메가, 빅세타에 대한 부분은 ratsgo.github에 잘 정리되어 있음