재귀 알고리즘

1. 재귀 ( Recursion )

• 어떠한 이벤트에서 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의되는 경우
• ex ) 자연수의 정의, 팩토리얼, 등비수열
• 연관 개념 : 병합 정렬, 퀵 정렬, 이진 검색 트리

※ 자연수의 정의
- 1은 자연수입니다.
- 어떤 자연수의 바로 다음 수도 자연수입니다.

2. 팩토리얼

• 재귀를 사용하는 대표적인 예
• 양의 정수를 순서대로 곱한다는 의미로 순차 곱셈이라고도 함

※ 팩토리얼 n!의 정의 ( n은 양의 정수 )
- 0! = 1
- n > 0 이면 n! = n * ( n - 1 )!

const factorial = (n: number): number => {
    if (n > 0) {
        return n * factorial(n - 1);
    } else {
        return 1;
    }
};

console.log(factorial(5)); // 120

3. 직접 재귀와 간접 재귀

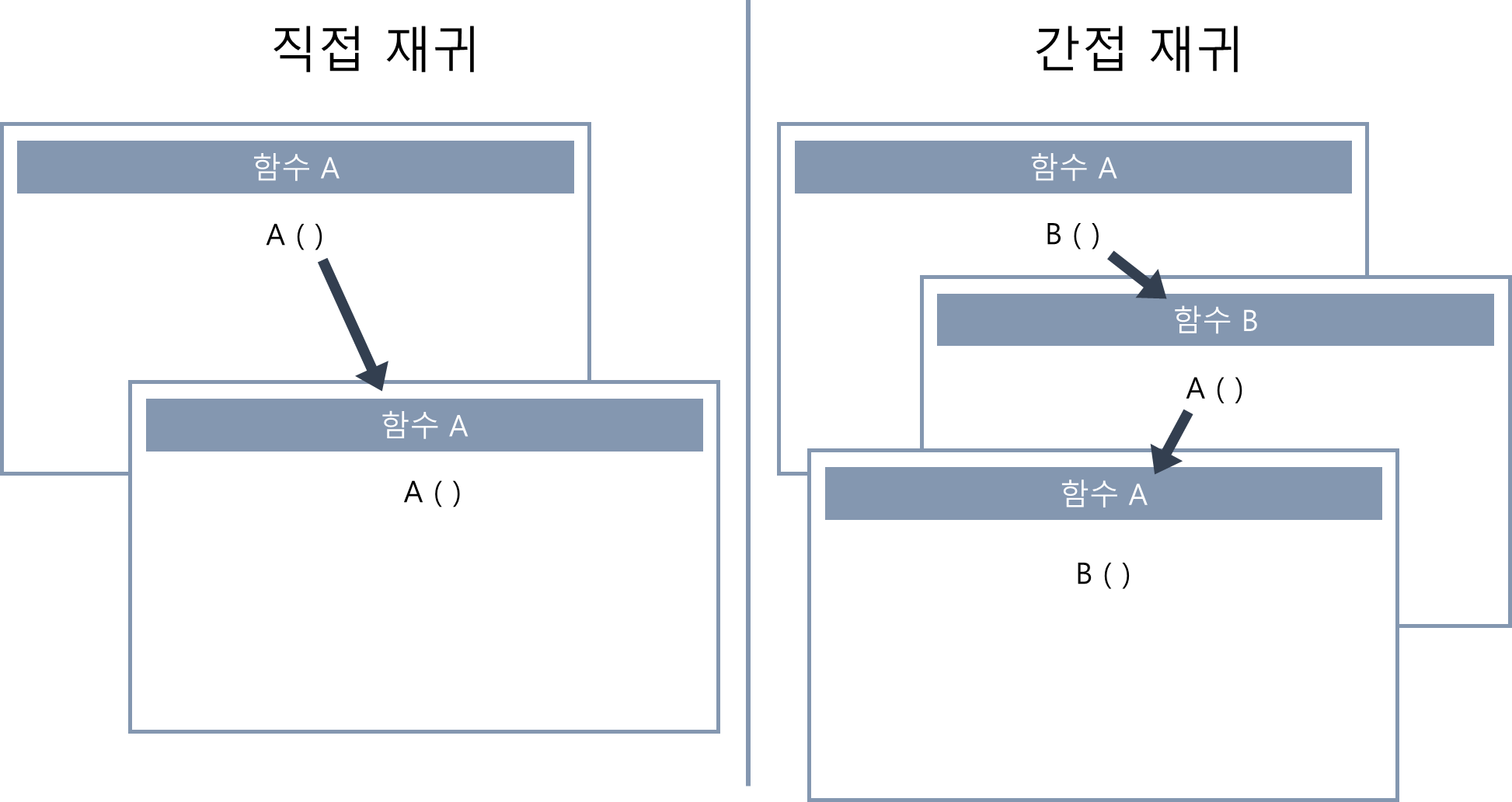
1 ) 직접 재귀

• direct recursion
• 자신과 똑같은 함수를 호출하는 방식

2 ) 간접 재귀

• indirect recursion
• A 함수가 B 함수를 호출하고, 다시 B 함수가 A 함수를 호출하는 구조
  

4. 유클리드 호제법

• Euclidean algorithm
• 2개의 자연수 또는 정식의 최대공약수 ( GCD ) 를 구하는 알고리즘
• GCD : Greatest Common Divisor
• 큰 값을 작은 값으로 나누어 떨어지면 작은 값이 최대 공약수가 됨
• 큰 값을 작은 값으로 나누어 떨어지지 않으면 작은 값과 나머지에 대해 같은 과정을 반복

const getGCD = (x: number, y: number): number => {
    if (y === 0) {
        return x;
    } else {
        return getGCD(y, x % y);
    }
};

console.log(getGCD(22, 8)); // 2

5. 하향식 분석과 상향식 분석

1 ) 순수한 재귀

• Genuinely recursion
• 재귀 호출을 여러 번 실행하는 함수

const recur = (n:number): void => {
    if (n > 0) {
        recur(n - 1);
        console.log(n);
        recur(n - 2);
    }
};

recur(4);

// 1 -> 2 -> 3 -> 1 -> 4 -> 1 -> 2

// recur(4) 
// -> recur(3) -> recur(2) -> recur(1) 
// -> recur(0) -> console.log(1) -> recur(-1) 
// -> console.log(2) -> recur(0) 
// -> console.log(3) -> recur(1) -> recur(0) -> console.log(1) -> recur(-1) 
// -> console.log(4) -> recur(2) -> recur(1) 
// -> recur(0) -> console.log(1) -> recur(-1) 
// -> console.log(2) -> recur(0) 

2 ) 하향식 분석

• top-down analysis
• 가장 위쪽에 위치한 상자의 함수 호출부터 시작하여 계단식으로 자세히 조사해 나가는 분석 방법

recur(4)의 실행 과정

1. recur(3)을 실행합니다.
2. 4를 출력합니다.
3. recur(2)을 실행합니다.

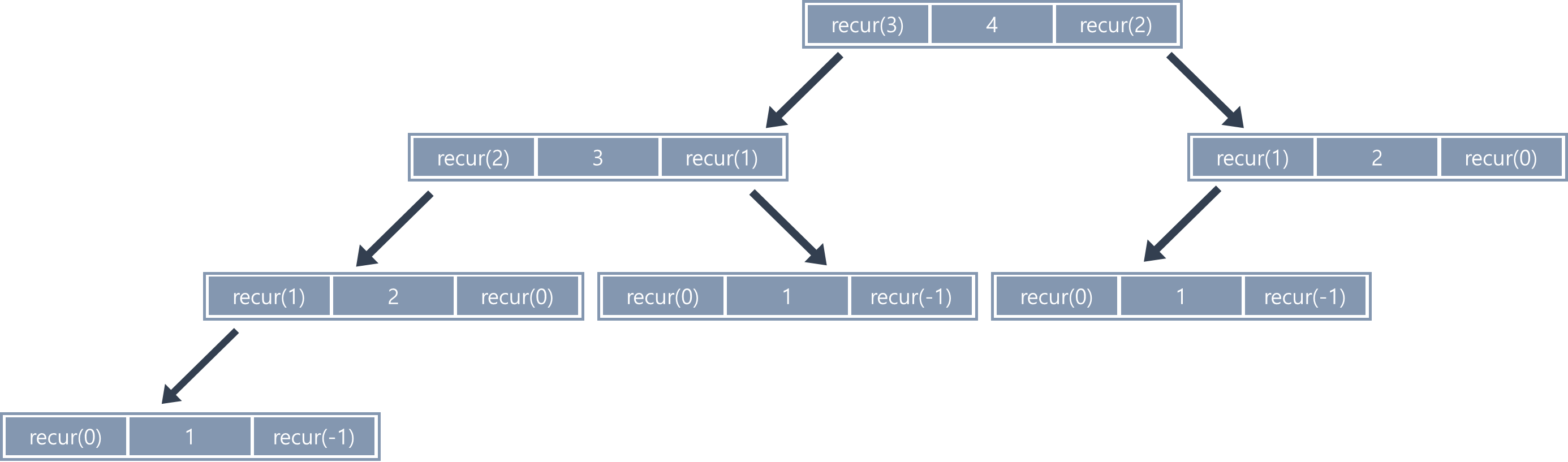
☑ 왼쪽 화살표를 따라 1칸 아래쪽 상자로 이동하고, 다시 원래 호출한 상자로 되돌아오면 값을 출력
☑ 오른쪽 화살표를 따라 1칸 아래쪽 상자로 이동한다.

위의 단 계를 1번 끝내야 비로소 1칸 위쪽 상자로 올라갈 수 있다.

3 ) 상향식 분석

• bottom-up analysis
• 아래쪽부터 쌓아 올리며 분석하는 방법

recur(1)의 실행 과정

1. recur(0)을 실행합니다.
2. 1을 출력합니다.
3. recur(-1)을 실행합니다.

☑ recur(0)과 recur(-1)은 출력할 내용이 없으므로 결국 1만 출력

recur(2)의 실행 과정

1. recur(1)을 실행합니다.
2. 2를 출력합니다.
3. recur(0)을 실행합니다.

☑ recur(1)은 1을 출력하지만 recur(0)은 아무것도 출력하지 않음

recur(-1) : 아무것도 하지 않음
recur(0)  : 아무것도 하지 않음
-------------------------------------------
recur(1)  : recur(0) 1️⃣ recur(-1) → 1️⃣
recur(2)  : recur(1) 2️⃣ recur(0)  → 1 2️⃣
recur(3)  : recur(2) 3️⃣ recur(1)  → 1 2 3️⃣ 1
recur(4)  : recur(3) 4️⃣ recur(2)  → 1 2 3 1 4️⃣ 1 2

6. 하노이의 탑

• towers of Hanoi
• 작은 원반이 위에, 큰 원반이 아래에 위치하는 규칙을 지키면서 기둥 3개를 이용해서 원반을 옮기는 문제
• 먼저 크기가 모두 다른 원반이 첫 번째 기둥에 쌓여 있는 상태로 시작
• 모든 원반을 세 번째 기둥에 최소 횟수로 옮기면 됨

1 ) 원반이 2개일 경우

1. 위의 원반을 중간 기둥으로 이동
2. 아래의 원반을 목표 기둥으로 이동
3. 위의 원반을 목표 기둥으로 이동

2 ) 원반이 3개일 경우

1. 위의 원반 두 개를 중간 기둥으로 옮김
2. 마지막 원반을 목표 기둥으로 옮김
3. 중간 기둥의 원반 두 개를 목표 기둥으로 옮김

3 ) 원반이 4개일 경우

1. 위의 원반 세 개를 중간 기둥으로 옮김
2. 마지막 원반을 목표 기둥으로 옮김
3. 중간 기둥의 원반 세 개를 목표 기둥으로 옮김

const move = (n: number, x: number, y: number): void => {
    const middle = 6 - x - y;
    if (n > 1) {
        move(n - 1, x, middle);
    }
    console.log(`원반 ${n}을 ${x} 기둥에서 ${y} 기둥으로 이동`);
    if (n > 1) {
        move(n - 1, middle, y);
    }
};

move(3, 1, 3);

// 원반 1을 1 기둥에서 3 기둥으로 이동
// 원반 2을 1 기둥에서 2 기둥으로 이동
// 원반 1을 3 기둥에서 2 기둥으로 이동
// 원반 3을 1 기둥에서 3 기둥으로 이동
// 원반 1을 2 기둥에서 1 기둥으로 이동
// 원반 2을 2 기둥에서 3 기둥으로 이동
// 원반 1을 1 기둥에서 3 기둥으로 이동

7. 8퀸 문제

• 8-Queen problem
• 19세기의 수학자 가우스가 오답을 발표한 것으로 유명
• 8개의 퀸이 서로 공격하여 잡을 수 없도록 8X8 체스판에 배치
  ※ 퀸은 체스판의 가로, 세로, 대각선 어디든지 8개의 방향으로 직선 이동해서 상대를 잡을 수 있음

1 ) 한정 작업과 분기 한정법

한정 작업

• branching
• 가지가 뻗어 나가듯이 배치 조합을 열거하는 방법

분기 한정법

• divide and conquer
• 큰 문제를 작은 문제로 분할하고, 작은 문제 풀이법을 결합하여 전체 풀이법을 얻는 방법
• 문제를 분할할 때 작은 문제 풀이법에서 원래의 문제 풀이법을 쉽게 도출할 수 있도록 설계해야 함

2 ) 퀸 배치하기

case 1 랜덤으로 배치하기

64 x 63 x 62 x 61 x 60 x 59 x 58 x 57 = 178,462,987,637,760

☑ 이 모든 경우의 수를 확인하는 것은 비현실적

case 2 각 열에 1개만 배치하기

8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 = 16,777,216

pos라는 배열을 이용하여 queen의 위치 표시
pos의 인덱스가 열, 값이 행을 의미

const pos = new Array(8).fill(0);

const put = (): void => {
    console.log(...pos);
};

const set = (i: number): void => {
    for (let j = 0; j < 8; j++) {
        pos[i] = j;
        if (i === 7) put();
        else set(i + 1);
    }
};

set(0);

☑ 퀸은 자신과 같은 행에 있는 다른 퀸을 공격하는 것이 가능하다

case 3 각 행에도 1개씩만 배치하기

8! = 40.320

pos라는 배열을 이용하여 queen의 위치 표시
flag 배열을 통해 해당 행에 이미 배치된 queen이 있는지 확인

const pos = new Array(8).fill(0);
const flag = new Array(8).fill(false);

const put = () => {
    console.log(...pos);
};

const set = (i) => {
    for (let j = 0; j < 8; j++) {
        if (!flag[j]) {
            pos[i] = j;
            if (i === 7) put();
            else {
                flag[j] = true;
                set(i + 1);
                flag[j] = false;
            }
        }
    }
};

set(0);

case 4 대각선에도 1개씩만 배치하기

pos라는 배열을 이용하여 queen의 위치 표시
flag_a 배열을 통해 해당 행에 이미 배치된 queen이 있는지 확인
flag_b 배열을 통해 우상향, 좌하향 대각선 방향으로 queen이 있는지 확인
flag_c 배열을 통해 우하향, 좌상향 대각선 방향으로 queen이 있는지 확인

const pos = new Array(8).fill(0);
const flag_a = new Array(8).fill(false);
const flag_b = new Array(15).fill(false);
const flag_c = new Array(15).fill(false);

const put = () => {
    console.log(...pos);
};

const set = (i) => {
    for (let j = 0; j < 8; j++) {
        const B_IDX = i + j;
        const C_IDX = i - j + 7;
        if (!flag_a[j] && !flag_b[B_IDX] && !flag_c[C_IDX]) {
            pos[i] = j;
            if (i === 7) put();
            else {
                flag_a[j] = flag_b[B_IDX] = flag_c[C_IDX] = true;
                set(i + 1);
                flag_a[j] = flag_b[B_IDX] = flag_c[C_IDX] = false;
            }
        }
    }
};

set(0);