1. 정렬
정렬 ( Sorting )
키 ( key )를 항목값의 대소 관계에 따라 데이터 집합을 일정한 순서로 바꾸어 늘어놓는 작업
정렬 분류하기
1 ) 오름차순과 내림차순
오름차순 ( ascending order ) : 값이 작은 데이터를 앞쪽에 늘어놓는 것
내림차순 ( descending order ) : 값이 큰 데이터를 앞쪽에 늘어놓는 것
2 ) 안정성
안정적인 알고리즘 ( stable algorithm ) : 값이 같은 원소의 순서가 정렬 후에도 유지되는 것
3 ) 내부 정렬과 외부 정렬
내부 정렬 ( internal sorting ) : 모든 데이터를 하나의 배열에 저장할 수 있는 경우에 사용하는 알고리즘
외부 정렬 ( external sorting ) : 정렬할 데이터가 많아서 하나의 배열에 저장할 수 없는 경우에 사용하는 알고리즘
2. 버블 정렬
버블 정렬 ( Bubble Sort )
이웃한 두 원소의 대소 관계를 비교하여 필요에 따라 교환을 반복하는 알고리즘
단순 교환 정렬이라고도 함
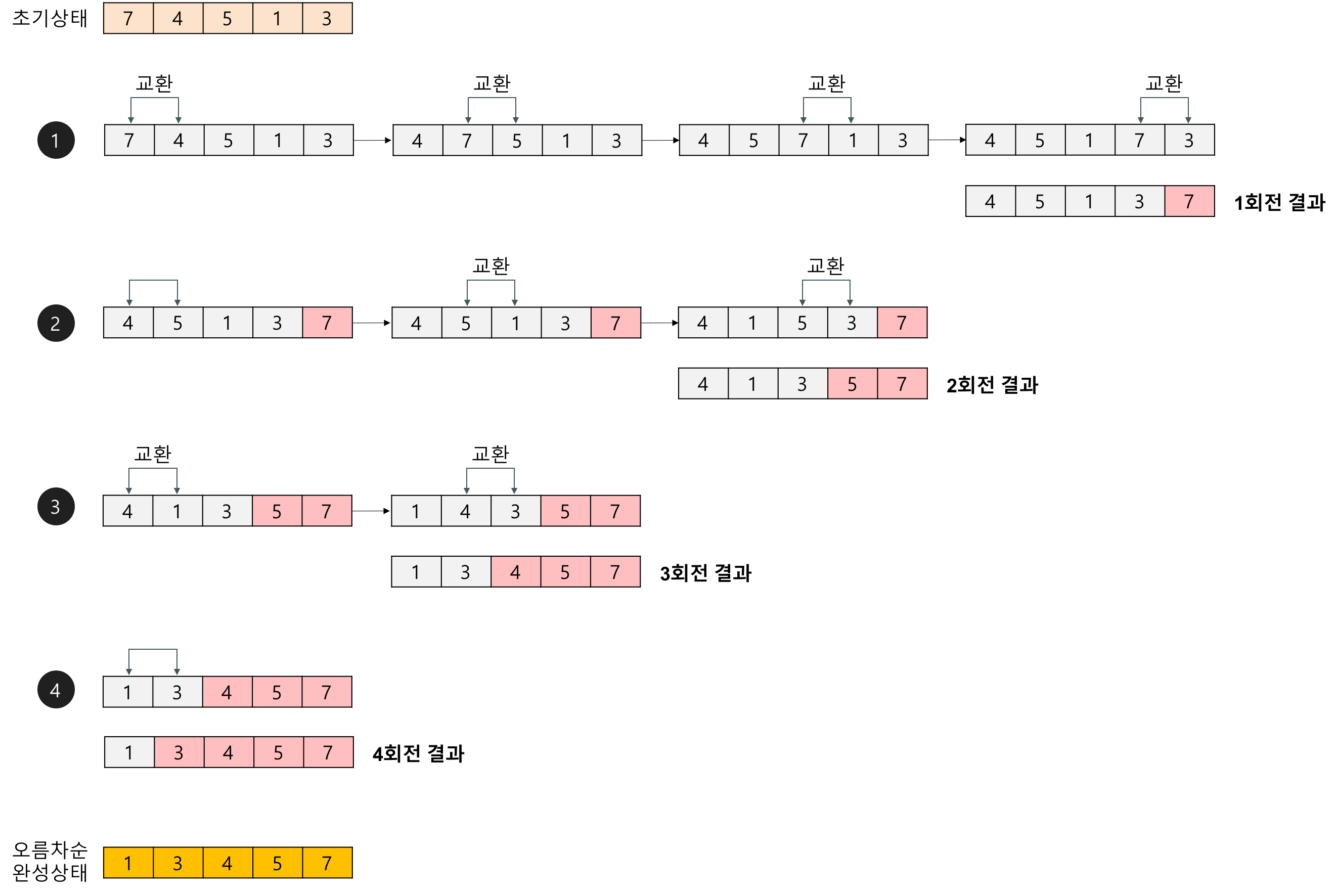
이미지 출처 : https://gmlwjd9405.github.io/2018/05/06/algorithm-bubble-sort.html
기본 버블 정렬 구현해보기
기본 과정
- 시작점을 잡는다. ( 맨 앞 또는 맨 뒤 )
- 정렬 방식을 결정한다. ( ex. 오름차순 )
- 시작점과 시작점 바로 옆 원소를 비교한다.
- 교환이 필요하면 교환한다.
- 시작점 바로 옆 원소와 그 다음 원소를 비교한다. ( 총 n - 1 번 비교 )
- 배열의 끝까지 위의 과정을 반복한다.
- 배열의 끝은 정렬이 완료되었다.
- 다시 시작점부터 비교를 시작한다.
- 배열의 끝 바로 전 정렬이 완료되었다.
- 모든 원소의 정렬이 완료될 때까지 반복한다. ( 총 n ( n -1 ) / 2 번 비교 )
패스 ( pass )
일련의 비교 및 교환하는 과정
시작점부터 정렬이 완료된 부분 앞까지 비교 및 교환 과정이 하나의 패스이다.
구현해보기
const bubbleSort = (arr: number[]) => {
const n = arr.length;
for (let i = 0; i < n - 1; i++) {
for (let j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
const temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
console.log(arr);
}
}
};
bubbleSort([5, 4, 3, 2, 1]);
// [ 4, 5, 3, 2, 1 ]
// [ 4, 3, 5, 2, 1 ]
// [ 4, 3, 2, 5, 1 ]
// [ 4, 3, 2, 1, 5 ]
// [ 3, 4, 2, 1, 5 ]
// [ 3, 2, 4, 1, 5 ]
// [ 3, 2, 1, 4, 5 ]
// [ 2, 3, 1, 4, 5 ]
// [ 2, 1, 3, 4, 5 ]
// [ 1, 2, 3, 4, 5 ]위의 알고리즘의 문제점
이미 이후 요소들이 정렬된 상태이면 불필요한 연산을 하게 됨
const bubbleSort = (arr: number[]) => {
const n = arr.length;
for (let i = 0; i < n - 1; i++) {
let exchangeCount = 0;
for (let j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
const temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
exchangeCount++;
}
console.log(arr);
}
if (!exchangeCount) {
break;
}
}
};
bubbleSort([6, 4, 3, 7, 1, 9, 8]);
// [4, 6, 3, 7, 1, 9, 8]
// [4, 3, 6, 7, 1, 9, 8]
// [4, 3, 6, 7, 1, 9, 8]
// [4, 3, 6, 1, 7, 9, 8]
// [4, 3, 6, 1, 7, 9, 8]
// [4, 3, 6, 1, 7, 8, 9]
// [3, 4, 6, 1, 7, 8, 9]
// [3, 4, 6, 1, 7, 8, 9]
// [3, 4, 1, 6, 7, 8, 9]
// [3, 4, 1, 6, 7, 8, 9]
// [3, 4, 1, 6, 7, 8, 9]
// [3, 4, 1, 6, 7, 8, 9]
// [3, 1, 4, 6, 7, 8, 9]
// [3, 1, 4, 6, 7, 8, 9]
// [3, 1, 4, 6, 7, 8, 9]
// [1, 3, 4, 6, 7, 8, 9]
// [1, 3, 4, 6, 7, 8, 9]
// [1, 3, 4, 6, 7, 8, 9]
// [1, 3, 4, 6, 7, 8, 9]
// [1, 3, 4, 6, 7, 8, 9]위의 알고리즘의 문제점
뒷 부분의 요소들이 정렬되어 있으면 불필요한 비교를 하게 됨
해결법 나중에 추가셰이커 정렬
셰이커 정렬 ( Shaker Sort )
버블 정렬을 개선한 알고리즘
양방향 버블 벙렬 ( Bidirectional Bubble Sort )
칵테일 정렬 ( Cocktail Sort )
칵테일 셰이커 정렬 ( Cocktail Shaker Sort )
3. 단순 선택 정렬
단순 선택 정렬 ( Straight Selection Sort )
가장 작은 원소부터 선택해 알맞은 위치로 옮기는 작업을 반복하며 정렬하는 알고리즘
과정
1. 아직 정렬하지 않은 부분에서 값이 가장 작은 원소를 선택한다.
2. 아직 정렬하지 않은 부분에서 맨 앞에 있는 원소를 교환한다.
단순 선택 정렬은 서로 이웃하지 않는 떨어져 있는 원소를 교환하므로 안정적이지 않다.
구현해보기
const selectionSort = (arr: number[]) => {
const n = arr.length;
for (let i = 0; i < n - 1; i++) {
let min = i;
for (let j = i + 1; j < n; j++) {
if (arr[j] < arr[min]) min = j;
}
const temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
console.log(arr, i, min);
}
};
selectionSort([5, 4, 3, 2, 1]);
// [ 1, 4, 3, 2, 5 ] 0 4
// [ 1, 2, 3, 4, 5 ] 1 3
// [ 1, 2, 3, 4, 5 ] 2 2
// [ 1, 2, 3, 4, 5 ] 3 34. 단순 삽입 정렬
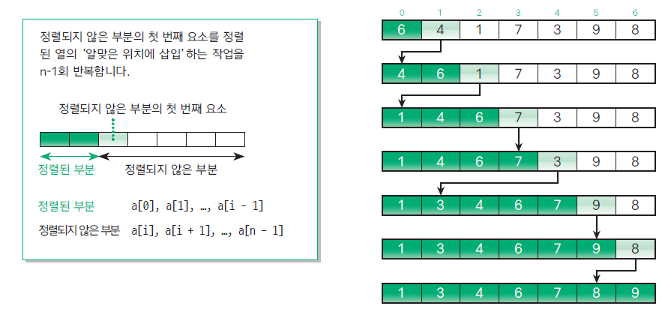
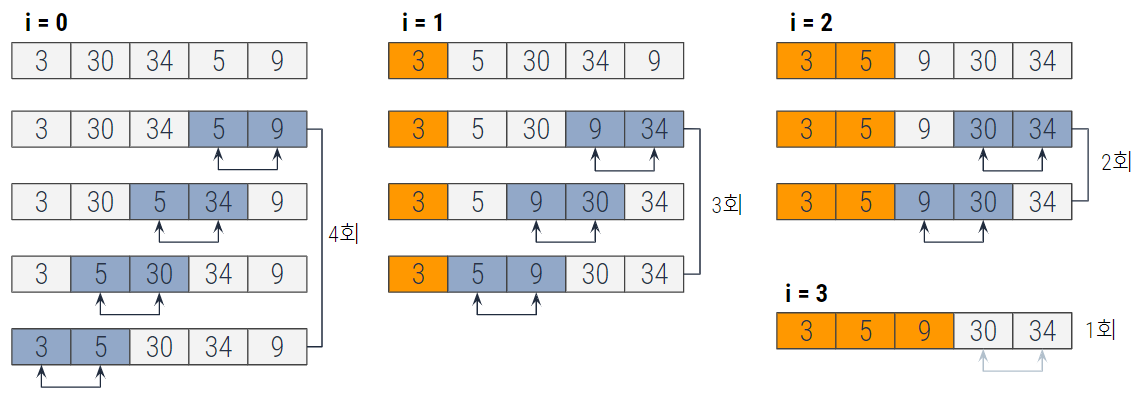
** 단순 삽입 정렬 ( Straight Insertion Sort )
주목한 원소보다 더 앞쪽에서 알맞은 위치로 삽입하며 정렬하는 알고리즘
종료 조건
① 정렬된 배열의 왼쪽 끝에 도달한 경우
② temp 보다 작거나 키값이 같은 원소를 발견할 경우
계속 조건
① 인덱스가 0보다 큰 경우
② 현재 값이 temp보다 큰 경우
구현해보기
const insertionSort = (arr: number[]) => {
const n = arr.length;
for (let i = 1; i < n; i++) {
let index = i;
const temp = arr[i];
while (index > 0 && arr[index - 1] > temp) {
arr[index] = arr[index - 1];
index--;
}
arr[index] = temp;
console.log(arr);
}
};
insertionSort([6, 4, 3, 7, 1, 9]);
// [ 4, 6, 3, 7, 1, 9 ]
// [ 3, 4, 6, 7, 1, 9 ]
// [ 3, 4, 6, 7, 1, 9 ]
// [ 1, 3, 4, 6, 7, 9 ]
// [ 1, 3, 4, 6, 7, 9 ]단순 정렬 알고리즘의 시간 복잡도는 모두 O(n²)으로 프로그램의 효율이 좋지 않다.
5. 셸 정렬
셸 정렬 ( Shell Sort )
단순 삽입 정렬의 장점은 살리고 단점은 보완하여 더 빠르게 정렬하는 알고리즘
단순 삽입 정렬의 장단점
장점 : 이미 정렬을 마쳤거나 정렬이 거의 끝나가는 상태에서는 속도가 매우 빠르다.
단점 : 삽입할 위치가 멀리 떨어져 있으면 이동 횟수가 많아진다.
셸 정렬
- 도널드 L. 셸이 고안한 알고리즘으로 정렬할 배열의 원소를 그룹으로 나눠 각 그룹별로 정렬을 수행한다.
- 정렬된 그룹을 합치는 작업을 반복하여 원소의 이동 횟수를 줄이는 방법
예시 배열 : [ 8, 1, 4, 2, 7, 6, 3, 5 ]
Step 1. 4-정렬
서로 4칸 떨어진 원소를 정렬하는 방법을 '4-정렬'이라 한다.
[ 8, 1, 4, 2, 7, 6, 3, 5 ]
=> [ 7, 1, 4, 2, 8, 6, 3, 5 ]
[ 7, 1, 4, 2, 8, 6, 3, 5 ]
=> [ 7, 1, 4, 2, 8, 6, 3, 5 ]
[ 7, 1, 4, 2, 8, 6, 3, 5 ]
=> [ 7, 1, 3, 2, 8, 6, 4, 5 ]
[ 7, 1, 3, 2, 8, 6, 4, 5 ]
=> [ 7, 1, 3, 2, 8, 6, 4, 5 ]Step 2. 2-정렬
[ 7, 1, 3, 2, 8, 6, 4, 5 ]
=> [ 3, 1, 4, 2, 7, 6, 8, 5 ]
[ 3, 1, 4, 2, 7, 6, 8, 5 ]
=> [ 3, 1, 4, 2, 7, 5, 8, 6 ]Step 3. 1-정렬
[ 3, 1, 4, 2, 7, 6, 8, 5 ]
=> [ 1, 2, 3, 4, 5, 6, 7, 8 ]셸 정렬 과정에서 수행하는 각각의 정렬을 h-정렬이라고 한다.
위의 예시는 h값을 4, 2, 1로 감소시키면서 정렬을 총 7번 수행하여 정렬을 완료한다.
구현해보기
const shellSort = (arr: number[]) => {
const n = arr.length;
let h = parseInt(n / 2);
while (h > 0) {
for (let i = h; i < n; i++) {
let index = i - h;
const temp = arr[i];
while (index >= 0 && arr[index] > temp) {
arr[index + h] = arr[index];
index -= h;
}
arr[index + h] = temp;
}
h = parseInt(h / 2);
console.log(arr);
}
};
shellSort([8, 1, 4, 2, 7, 6, 3, 5]);
// [ 7, 1, 3, 2, 8, 6, 4, 5 ]
// [ 3, 1, 4, 2, 7, 5, 8, 6 ]
// [ 1, 2, 3, 4, 5, 6, 7, 8 ]h 값이 서로 배수이거나 초깃값이 너무 클 경우 효과적으로 정렬되지 않는다.
const shellSort = (arr: number[]) => {
const n = arr.length;
let h = 1;
console.log("arr :", arr);
while (h < parseInt(n / 9)) {
h = h * 3 + 1;
}
console.log("h :", h);
while (h > 0) {
for (let i = h; i < n; i++) {
let index = i - h;
const temp = arr[i];
while (index >= 0 && arr[index] > temp) {
arr[index + h] = arr[index];
index -= h;
}
arr[index + h] = temp;
}
h = parseInt(h / 3);
console.log("arr :", arr);
console.log("h :", h);
}
};
shellSort([
8, 1, 4, 2, 7, 6, 3, 5, 9, 11,
14, 25, 13, 17, 20, 35, 1, 63, 2, 3465,
123, 6, 21, 35, 14, 234
]);
// arr : [
// 8, 1, 4, 2, 7, 6, 3, 5, 9, 11,
// 14, 25, 13, 17, 20, 35, 1, 63, 2, 3465,
// 123, 6, 21, 35, 14, 234
// ]
// h : 4
// arr : [
// 1, 1, 2, 2, 7, 6, 3, 5, 8, 6,
// 4, 25, 9, 11, 14, 35, 13, 17, 20, 35,
// 14, 63, 21, 3465, 123, 234
// ]
// h : 1
// arr : [
// 1, 1, 2, 2, 3, 4, 5, 6, 6, 7,
// 8, 9, 11, 13, 14, 14, 17, 20, 21, 25,
// 35, 35, 63, 123, 234, 3465
// ]
// h : 0