<Lv.3> 등산코스 정하기 (프로그래머스 : C#)

https://school.programmers.co.kr/learn/courses/30/lessons/118669

📕 문제 설명

n개의 지점으로 이루어진 산이 있다. 출입구, 쉼터, 산봉우리로 이루어져 있으며 각 지점은 양방향 통행이 가능하다. 서로 다른 지점으로 이동할 때 등산로별로 일정 시간이 소요된다.

출입구 중 한 곳에서 출발해 산봉우리 중 한 곳만 방문 후 다시 원래의 출입구로 돌아오는 등산코스를 정할 때 가장 낮은 intensity를 가지는 등산 코스 정하기
(출입구는 처음과 끝에 한 번 포함, 산봉우리는 한 번만 포함)

(intensity = 등산코스를 따라 이동 중 쉼터 혹은 산봉우리 방문 시 휴식을 취할 수 있으며, 휴식 없이 이동해야하는 시간 중 가장 긴 시간)

paths[i, j, w]: i번과 j번 지점을 연결하는 등산로가 존재하며, w 시간이 걸림

• Input
  XX산의 지점 수, 각 등산로 정보, 출입구 번호, 산봉우리 번호
• Output
  intensity가 최소가 되는 등산코스에 포함된 산봉우리 번호와 intensity의 최솟값 (intensity가 최소가 되는 등산코스가 여러개라면 그 중 산봉우리의 번호가 가장 낮은 등산코스 선택)

예제

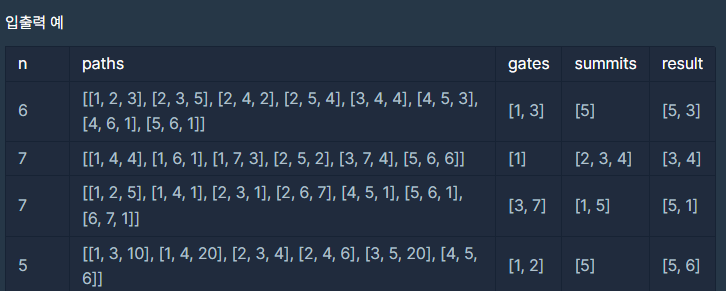
풀이

우선 순위 큐에서 intensity가 낮은 것을 기준으로 뽑는다. 출입구를 하나만 사용해야 하므로 intensity를 0으로해서 먼저 우선 순위 큐에 다 넣어준다. intensity가 낮은 것의 인접한 것들을 기준에 맞춰 넣어주며 탐색을 진행한다. 이때 summit도 한번만 들려야 하기 때문에 summit을 만나고 최소의 intensity가 보장되는 경우 답을 갱신해준다. (summit과 인접한 것을 굳이 우선 순위 큐에 넣지 않는 이유는 어차피 최소의 intensity를 가지는 길로 왔기 때문에 돌아가는 것도 이것이 최소이므로 더 볼 필요가 없다.)

using System;
using System.Collections.Generic;
using System.Linq;

public class Solution
{
    public int[] solution(int n, int[,] paths, int[] gates, int[] summits)
    {
        int[] dist = new int[50001]; // 각 노드의 최소 intensity
        List<List<int>>[] graph = new List<List<int>>[50001];
        HashSet<int> summitSet = new HashSet<int>(summits);
        int[] ans = new int[2] {-1,-1}; // 정답 배열
        
        Array.Fill(dist, Int32.MaxValue); // dist -1로 초기화
        // 그래프 초기화
        for (int i = 0; i <= n; i++) graph[i] = new List<List<int>>();
        for (int i = 0; i < paths.GetLength(0); i++)
        {
            graph[paths[i,0]].Add(new List<int>() {paths[i,1], paths[i,2]});
            graph[paths[i,1]].Add(new List<int>() {paths[i,0], paths[i,2]});
        }
        
        PriorityQueue pq = new PriorityQueue();
        
        foreach (int gate in gates) // 출입구 -> pq
        {
            pq.Enqueue(0, gate);
            dist[gate] = 0;
        }

        while (pq.Count >= 1)
        {
            (int currIntensity, int currNode) = pq.Dequeue(); // minHeap (intensity)

			// 이미 더 작은 intensity로 본적 있다면 pass
            if (currIntensity > dist[currNode]) continue;
            
            // 현재 최소 intensity보다 더 큰 경우 pass
            if (ans[0] != -1 && ans[1] < currIntensity) continue;
            
            // summit인 경우 => 정답 갱신할지 확인
            if (summitSet.Contains(currNode))
            {
                if(ans[0] == -1 || ans[1] > currIntensity) // 최소가 되는 경우
                {
                    ans[0] = currNode;
                    ans[1] = currIntensity;
                }
                // 산봉우리 번호 낮은 것으로 갱신 (intensity 같으면)
                else if(ans[1] == currIntensity && ans[0] > currNode) ans[0] = currNode;
                continue;
            }
            
            // 인접 노드 탐색
            for (int i = 0; i < graph[currNode].Count; i++)
            {
                int adjNode = graph[currNode][i][0];
                int adjW = graph[currNode][i][1];
                // 현재 intensity와 다음 노드 w 중 더 큰 값
                int newIntensity = Math.Max(currIntensity, adjW);
				
                // 위의 값이 저장된 dist보다 작으면 갱신
                if (newIntensity < dist[adjNode])
                {	
                    dist[adjNode] = newIntensity;
                    pq.Enqueue(newIntensity, adjNode);
                }
            }
        }

        return ans;
    }
}

public class PriorityQueue // MinHeap
{
    private List<(int, int)> heap = new List<(int, int)>();

    public int Count => heap.Count;
    
    public void Enqueue(int intensity, int node)
    {
        heap.Add((intensity, node));
        int now = heap.Count - 1; // 추가한 노드 위치 (트리 마지막 레벨 왼쪽)
        
        while (now > 0) // 순서 지정하기
        {
            int next = (now - 1) / 2; // 부모 노드 (트리)
            if (heap[now].Item1 >= heap[next].Item1) break;
            // 부모노드보다 추가한게 작으면 Swap
            var temp = heap[now];
            heap[now] = heap[next];
            heap[next] = temp;
            now = next;
        }
    }
    
    public (int, int) Dequeue()
    {
        var ret = heap[0]; // return할 값 (트리 root에 max 저장해둔 형태)
        int lastIndex = heap.Count - 1;
        heap[0] = heap[lastIndex];
        heap.RemoveAt(lastIndex);
        lastIndex -= 1;
        int now = 0;
        
        while (true)
        {
            int left = 2 * now + 1;
            int right = 2 * now + 2;
            int next = now;
            
            if (left <= lastIndex && heap[next].Item1 >= heap[left].Item1) next = left; // 왼쪽보다 크면 왼쪽으로 보내기
            if (right <= lastIndex && heap[next].Item1 >= heap[right].Item1) next = right; // 오른쪽보다 크면 오른쪽으로 보내기 (여기서는 위에 now랑 left랑 비교해서 더 큰애랑 또 비교해서 갱신하게됨)
            if (next == now) break;
            
            var temp = heap[now];
            heap[now] = heap[next];
            heap[next] = temp;
            
            now = next;
        }
        
        return ret;
    }
}

결과