<Lv.3> 사라지는 발판 (프로그래머스 : C#)

https://school.programmers.co.kr/learn/courses/30/lessons/92345

📕 문제 설명

게임에서 양 플레이어가 최적의 플레이를 진행한다. 이길 수 있는 플레이어는 최대한 빨리 승리하도록 플레이하고, 질 수 밖에 없는 플레이어는 최대한 오래 버티도록 플레이 한다. 두 캐릭터가 움직인 횟수의 합을 반환하기

🔹 게임 규칙
캐릭터는 발판이 있는 곳으로만 이동할 수 있으며, 보드 밖으로는 이동 불가

밟고 있던 발판은 그 위의 캐릭터가 다른 발판을 밟음과 동시에 사라짐

양 플레이어는 번갈아가며 자신의 차례에 캐릭터를 상하좌우 인접한 발판으로 옮겨야함

🔹 게임 종료 조건
1. 움직일 차례에 상하좌우에 발판이 없는 경우
2. 두 캐릭터가 같은 발판 위에 있을 때, 상대 플레이어의 캐릭터가 다른 발판으로 이동하는 경우

• Input
  게임 보드 초기 상태, 플레이어 A의 캐릭터 초기 위치, 플레이어 B의 캐릭터 초기 위치
• Output
  두 캐릭터가 움직인 횟수의 합

예제

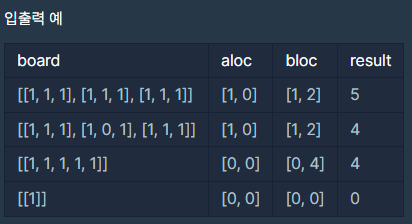
풀이

게임 이론의 Min Max tree 개념을 이용해 각 플레이어 별 최적의 행동을 결정한다.

상대가 무조건 이길 때는 최대한 늦게 지도록 값을 선택하며, 상대가 무조건 지는 경우 최대한 빨리 이기도록 값을 선택한다.

using System;

public class Solution {
    int[] dX = {-1, 1, 0, 0};
    int[] dY = {0, 0, -1 , 1};
    bool[,] visited = new bool[5,5];
    
    public int solution(int[,] board, int[] aloc, int[] bloc) {
        
        return GetMoveCount(aloc[0], aloc[1], bloc[0], bloc[1], board);
    }
    
    // 현재 플레이어, 상대 플레이어 넘기며 count 세기
    public int GetMoveCount(int myX, int myY, int otherX, int otherY, int[,] board)
    {
        if (visited[myX, myY]) return 0;
        int canWin = 0;
        visited[myX, myY] = true;
        
        for (int i = 0; i < 4; i++)
        {
            int newX = myX + dX[i];
            int newY = myY + dY[i];
            // 보드 범위 밖
            if (newX < 0 || newY < 0 || newX >= board.GetLength(0) || newY >= board.GetLength(1)) continue;
            // 발판 사라졌거나 없는 경우
            if (visited[newX, newY] || board[newX, newY] == 0) continue;
            
            // 현재 플레이어 기준 상대 플레이어로 턴 넘기기
            int otherMoveCount = GetMoveCount(otherX, otherY, newX, newY, board) + 1; // 상대의 결과가 지는 경우 (0) => 나는 이기는 것 (1), 상개가 이기는 경우 (1) => 나는 지는 것 (0)
            
            // 현재 저장된 값 패배, 상대가 지는 경우 => 이기는 경우로 저장
            if (canWin % 2 == 0 && otherMoveCount % 2 == 1) canWin = otherMoveCount;
            // 현재 저장된 값 패배, 상대가 이기는 경우 => 최대한 늦게 지도록
            else if (canWin % 2 == 0 && otherMoveCount % 2 == 0) canWin = Math.Max(canWin, otherMoveCount);
            // 현재 저장된 값 승리, 상대가 지는 경우 => 최대한 빨리 이기도록
            else if (canWin % 2 == 1 && otherMoveCount % 2 == 1) canWin = Math.Min(canWin, otherMoveCount);
        }
        
        visited[myX, myY] = false;
        
        return canWin;
    }
}

결과