진수

soomin·2021년 8월 13일

Java-Basic

목록 보기

8/13

컴퓨터는 이진수 밖에 모른다.

컴퓨터에게 진수란 전압의 단계를 의미한다.

컴퓨터에게 가장 적합한 진수는 2진수이며, 1 = 전기가 흐름이고 0 = 전기가 흐르지 않음 이다.

변수는 값을 할당하기위해 메모리공간에 이름을 지은 것이다. 우리가 값을 할당할 때에 10진수로 표현해서 값을 저장하지만, 컴퓨터는 2진수 밖에 모르기 때문에 10진수를 다시 2진수로 변환해서 변수에 저장한다.

10진법과 2진법

일상생활에서 가장 많이 사용하는 진법은 10진법으로 0~9 , 즉 10개의 수를 표현할 수 있다.

9 보다 큰, 즉 10진수가 표현하지 못하는 수로 넘어가면, "올림"이 발생한다.

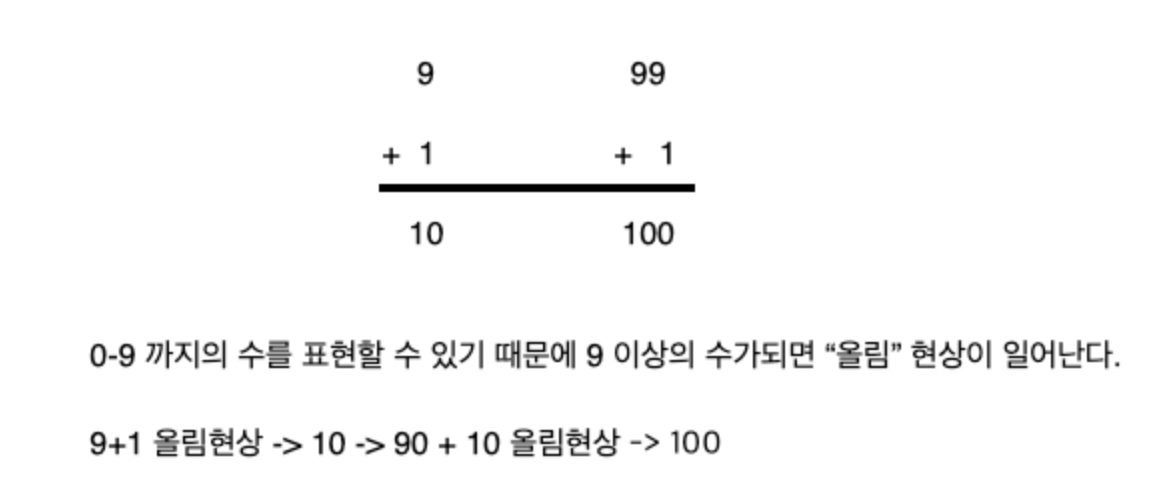
모든 진법에서 표현하는 수 이상을 넘어가게 되면 "올림"이 발생한다.
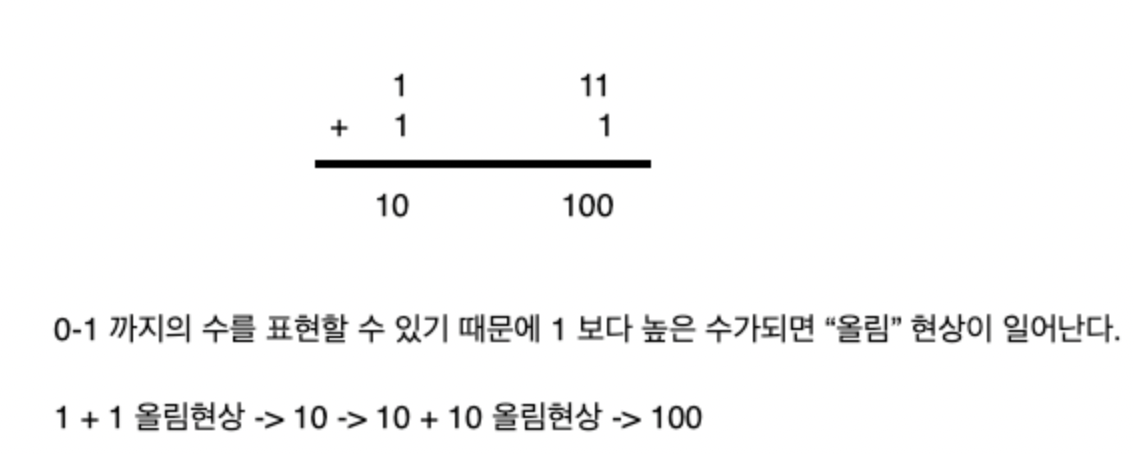
2 진법은 0-1 , 즉 2개의 수를 표현할 수 있으므로 1 보다 높은 수는 "올림"으로 표현한다.

bit 와 byte

1자리의 2진수를 표현할 수 있는 단위 를 bit 라고하며, 1bit 는 컴퓨터가 값을 저장할 수 있는 최소단위 이다.

8bit[2진수 8자리] 를 묶어 1byte 라고 하며, 1byte는 데이터의 기본단위 이다.

Word(워드)는 CPU 가 한 번에 처리할 수 있는 데이터의 크기를 의미한다.

Word 는 CPU 에 따라 다르며 32bit CPU 는 bit 32(4byte) 를 한 번에 처리할 수 있으며, 64bit CPU 는 64bit(8byte) 를 한 번에 처리할 수 있다.

하나의 바이트가 표현할 수 있는 값의 수는 2의 8승[8자리의 이진수]
→ 표현할 수 있는 가짓수를 곱한 것, 2x2x2x2x2x2x2x2

이를 일반화 시키면 n 비트로 2^n 만큼의 값을 표현할 수 있는 것이다.

n 비트로 표현할 수 있는 부호 없는 10 진수의 범위 : 0 ~ (2^n)-1
n 비트로 표현할 수 있는 값의 개수 : 2^n

8진법, 16진법

2진법으로도 10진수를 표현할 수 있으나, 표현할 수 있는 수의 한계 때문에 올림현상이 일어나 자릿수가 점점 더 많아진다. 이런 단점을 보완하기 위해서 8진법과 16진법을 사용한다.

8진법은 0~7, 16 진법은 0~F(15)까지의 값을 표현할 수 있으며, 더 큰 수는 올림처리 된다.

2진법은 2가지, 8진법은 8가지, 16진법은 16가지의 수를 표현하는데, 이렇게 계산하면..

2진법 2의 1승 가지의 수
8진법 2의 3승 가지의 수
16진법 2의 4승 가지의 수

대체할 수 있는 자릿 수를 파악해보면 이러하다.

8진법 2진수 3자리의 수를 대신한다.
16진법 2진수 4자리의 수를 대신한다.

2진수를 8진수 16진수로 변환

서론에 설명했던 것 처럼, 2진수 3자리를 8진수 1자리가 대신할 수 있고, 2진수 4자리를 16진수 1자리가 대신할 수 있다.

변환 방법은 이진수를 대신할 수 있는 자릿수만큼 뒤에서부터 끊어서 해당 진수로 변환하는 것이다.

1010101100 > 512+128+32+8+4 > 684 // [ 10진수 ]
1010101100 > 1_010_101_100 > 1_2_5_4 > 1254 // [ 8진수 ]
1010101100 > 10_1010_1100 > 2_A_C > 2AC // [ 16진수 ]

10 진수를 n 진수로 변환

10진수를 나눌 수 없을 때까지 진수 값으로 나눈 후, 몫 부터 나머지까지 순서대로 적어주면 된다.

public static void main(String[] args) {
        int num = 46;
        StringBuffer sb = new StringBuffer("");
        int n = 2;

        while (num >= n) {
            sb.append(num%n);
            num /= n;
        }
        sb.append(num);
        String result = sb.reverse().toString();

        System.out.println(result); // 101110
    }

n 진수를 10 진수로 변환

각 자리의 수 x 진수의 수^단위 을 구해서 더하면 된다.

public static void main(String[] args) {
    String arg = Integer.toBinaryString(46);
    int n = 2;//진수
		int result = 0;

    String[] strNum = arg.split("");

    result = strNum[strNum.length-1].equals("0") ?
								 0 : Integer.parseInt(strNum[strNum.length-1]);

    for(int i = 1; i < strNum.length; i++) {
        Integer number = Integer.valueOf(strNum[strNum.length - (i+1)]);
        int unit = 1;

        for(int j = 0; j < i; j++){
            unit *= n;
        }

        result += number * unit;
    }

    System.out.println("10 진수 변환 : "+result);
}

음수의 2진수 표현 - 2의 보수법

n 비트로 표현할 수 있는 값의 개수는 2^n 이다. 즉, 4bit 로 표현할 수 있는 값의 개수는 2^4=16가지의 수를 표현할 수 있다.

이 값을 부호 없는 정수(0, 양수)로 표현하면 다음과 같다.

이 때, 음수 표현을 위해 값의 가짓수를 절반으로 나누고
구분자로 가장 앞 bit를 기준으로 0은 양수, 1은 음수로 표현해보자

여기서 모순이 생긴다.
1. 0과 -0이 존재한다.
2. 2진수가 증가할 때, 10진 음수는 감소하고있다.

이 모순을 2의 보수법 을 이용하면 해결할 수 있다.

2의 보수법을 사용하면 10진수 기준으로 절댓값이 같은 2진수를 더하는 것으로 10진수 0을 도출할 수 있다.
또한, 2진수가 증가할 때 10진 음수도 증가하게 됬다.
-> 하지만 가장 앞 비트를 바꾸는 것으로 10진 양수의 음수를 표현할 수는 없어졌다.

2의 보수법

n의 보수 란 더했을 때 n이 되는 수를 의미한다. 3의 10의 보수는 7이며, 7의 10의 보수는 3이다.

이 때, 3과 7은 "10의 보수관계에 있다" 라고 한다.
그렇다면 2의 보수 란, "더했을 때 2가 되는 수" 를 의미하게 되며, 2진수 기준으로 2는 10이다.

2진수의 10(2)은 올림이 발생하는 수 이며,
2진수에서 2의 보수관계란 더했을 때 모든 단위에 올림이 발생하는 수를 의미한다.

해당 규칙을 10진수에 적용하면, 0101은 5 이고 1011은 -5가 되야한다.
이처럼 2의 보수관계에 있는 2진수를 "절댓값이 같고 부호가 다른 10진수로 표현하는 것"을 2의 보수법 이라고 한다.

10진 음수를 2진수로 표현하기

앞의 2의 보수법을 이해했다면 구하기 쉽다.
절댓값의 2진수의 2의 보수를 더하면 0000.. 10진수로 "0"이되므로, 절댓값의 2진수의 2의 보수는 해당 절댓값의 음수가 된다.

2의 보수를 구하는 법

이해는 했으나 구하는 법을 아직 모른다.
2진수의 2의보수, 즉 더해서 0이 되는 수는 2진수의 1의보수 +1 이 된다.

    public static void main(String[] args) {
        // 컴퓨터는 0 과 1만 알고 있으므로, 10진수 리터럴은 메모리에 2진수로 저장된다.

        int num = 5; // 0101

        // 이진수의 "1의 보수"는 더해서 모든 단위의 수가 1이 되는 수를 말한다.
        int num1 = ~num;
        // 이진수의 1의 보수 +1 은 "이진수의 2의 보수"가 된다. 이진수의 2의 보수는 더해서 0이 되는 수이다.
        int num2 = num + (num1+1);
        
        System.out.println(num2); //0
    }