😃[2주차 - Day1]😃

Linear system (선형시스템) ?
3x + y = 2
x - 2y = 3중학교 때 배운 소거법으로 위의 연립일차방정식을 간단히 해결할 수 있습니다.
이것을 정형화한 것이 Gauss 소거법입니다. Gauss 소거법에 대한 내용은 추후에 다룹니다.
3x + y + z = 4
x - 2y - z = 1
x + y + z = 2위의 연립일차방정식 또한 우리가 가지고 있는 지식 안에서 쉽게 해결할 수 있습니다.
하지만 식이 1000개 이상, 미지수가 몇천개 이상이면 어떻게 해야 일반적인 방법으로 풀이할 수 있는가에 대한 문제에 봉착하게 되었습니다.
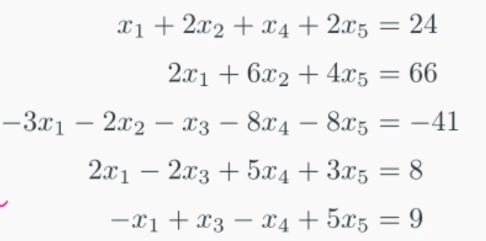
위의 식은 미지수(unknown)이 5개임에도 불구하고 한눈에 계산하기 어렵습니다.
어떤 연립일차방적식, 즉 linear system이어도 정형적인 방법으로 표현하고 해결하는 방법을 배우는 것이
선형 대수의 목표. Linear Algebra 입니다.
3x + y + z = 4
x - 2y - z = 1
x + y + z = 2위와 같은 형태의 방정식들을 각각 Linear equation(선형방정식) 이라고 합니다. 선의 형태라는 것을 표현하는 방법이죠.
평면에 올곧게 그려진다고 하면, 선형방정식이라고 합니다. 또한, 미지수들을 unknown (or variable) 이라고 부르기로 합니다.
3개의 Linear equations과 3개의 unknown으로 구성된 연립일차방정식을
3 x 3 linear system이라고 합니다.
미지수의 차수가 1차고, sin과 같은 특수한 경우가 아니라면 선형방정식으로 생각합니다.

xy+z=3이 수식은 선형방정식인가요, 비선형방정식인가요?
위와 같은 수식은 쌍곡선 형태로 그래프에 그려지는 걸 알고 있습니다. 또한 xy를 곱하게 되면 차수가 2차 이상으로 올라가기 때문에 선형방정식이 아니라는 것으로 귀결됩니다.
어떻게 하면 Ax=b 형태로 표현할 것인가 = 선형시스템의 대수적 표현 이라고 말합니다.
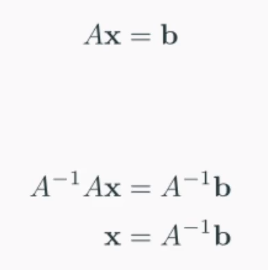
미지수를 열벡터 x로 표현하고, 계수를 모아 행벡터 형태 A로 표현, 상수를 모아 b에 표현하여 Ax=b로 나타내는 방식을 차용합니다.
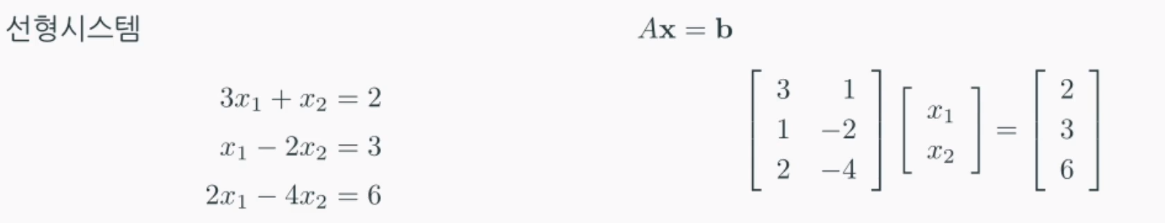
위와 같은 선형시스템은 3 x 2 선형시스템입니다.
Ax=b에서 A는 항상 m x n 행렬입니다. 이는 3 x 2 == m x n 으로 표현합니다.
Numpy 실습
A = np.array([[3,1,1], [1,-2,-1], [1,1,1]])
print(A)
print(np.shape(A))
b = np.array([4,1,2])
print(b)
print(np.shape(b))b는 세워져있는 열벡터라고 생각하셔도 무방합니다.
위와 같은 코드로 Ax=b를 표현하려고 합니다.
A-1Ax = A-1b 를 하여 결과를 구합니다.
역행렬 구하기
A_inv = np.linalg.inv(A)
print(A_inv)A-1를 위와같은 방식으로 구하여 곱해주기로 합니다.
역행렬을 이용한 선형시스템 Ax=b의 해 구하기
x = A_inv @ b
# x = np.matmul(A_inv, b)
print(x)
print(np.shape(x))결과 검증
# bb = np.matmul(A, x)
bb = A @ x
# @는 행렬과 행렬, 벡터와 벡터를 곱한다는 뜻
print(np.shape(bb))
print(bb)
if np.linalg.norm(b - bb) < 1e-3:
print("OK")
else:
print("Wrong!")b랑 bb의 차이가 거의 없다고 검증하면, 이 결과가 맞는지 아닌지 검증할 수 있습니다.
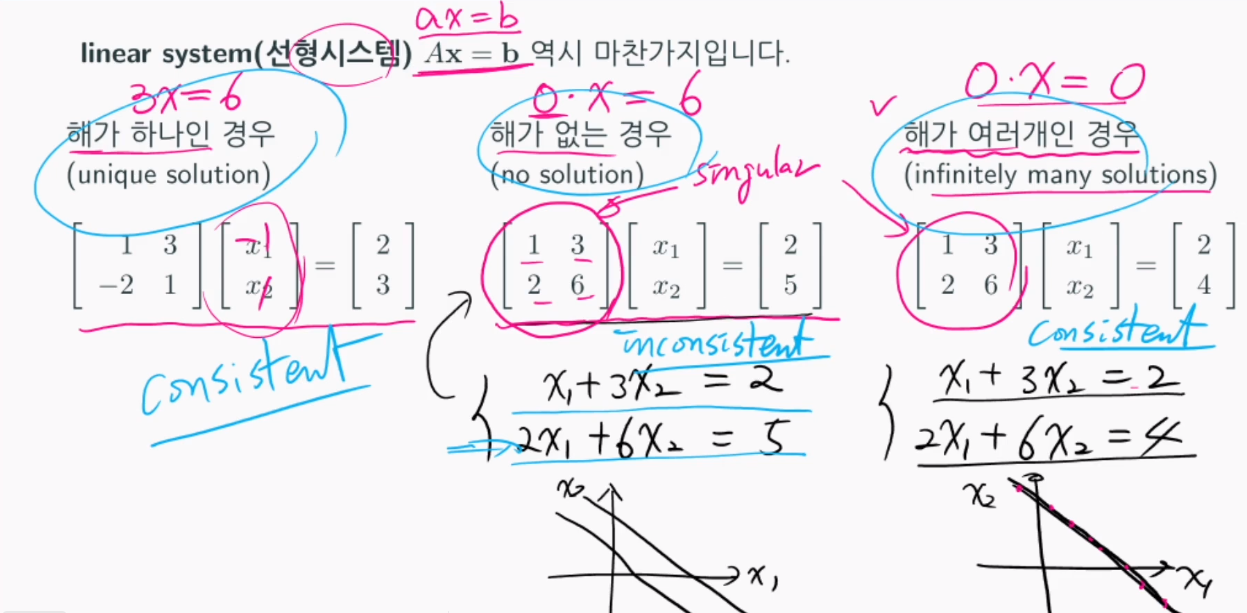
선형시스템의 Ax=b 문제를 살펴볼 때, A = 0일 경우 문제가 발생한다. a의 역수가 존재하지 않는 경우, a가 특이(singular)하다고 한다.
해가 있으면 선형시스템이 consistent하다고 하고, 해가 없으면 선형시스템이 inconsistent하다고 한다.
가우스 소거법
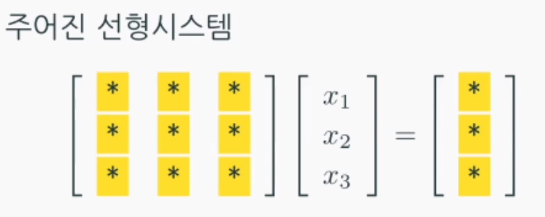
Gauss elimination (가우스 소거법)은 임의의 m x n 선형시스템의 해를 구하는 가장 대표적인 방법입니다. 가우스 소거법은 다음의 두 단계로 수행됩니다.
- Forward elimination (전방소거법): 주어진 선형시스템을 아래로 갈수록 더 단순한 형태의 선형방정식을 가지도록 변형한다. 중요
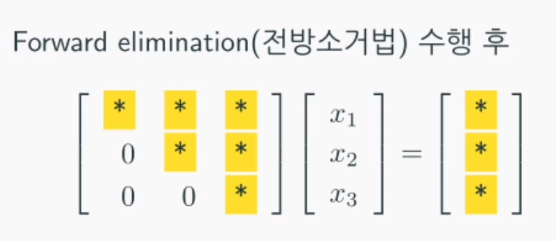
마지막 줄의 연산이 굉장히 간단해져서 x3의 결과를 쉽게 얻을 수 있습니다.
이를 알아내게되면 윗줄도 충분히 쉽게 얻을 수 있고 미지수를 모두 쉽게 알아낼 수 있다. 이를 후방대입법이라고 말합니다.
- Back-substitution (후방대입법): 아래에서부터 위로 미지수를 실제값으로 대체한다.
이러한 일련의 과정을 가우스 소거법이라고 합니다.
Elementary Row Operations ( EROs, 기본행연산 )

자세한 사항은 Numpy나 Scipy에 이미 이 방식대로 구현이 되어있습니다.
Forward Elimination (전방소거법)의 가치
rank라 하면, 식이 2개의 식인지 1개의 식인지 알려준다는 것!
(eg. 1x+2y = 1 이랑 2x+4y = 2랑은 하나의 식이다 라는 것)

또한 해가 있는지 없는지도 확인이 가능합니다.
