[알고리즘] 행렬의 곱셈 알고리즘

원래는 이과생이 아닌 문과생이였던 입장에서 행렬의 곱셈을 코드로 구현하고자 하였을 때, 적잖은 멘붕이 있었다. 따라서, 차근차근 복습하는 의미로 포스트를 남긴다.

1. 행렬의 곱셈이란?

말 그대로 두 행렬을 곱하는 것을 말한다. 가장 대표적으로 2×2행렬과 2×2행렬을 곱하는 것을 예시로 들어보겠다.

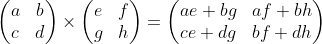
• 수정 : bf + dh 가 아닌 cf + dh

첫번째 행렬을 A, 두번째 행렬을 B, 결과 행렬을 C라고 해보자.

C의 i행 j열의 값 = A의 i행의 값 × B의 j열의 값

으로 정의할 수 있다.

이 예시의 경우, 곱하는 두 행렬의 행의 수와 열의 수가 똑같은 경우이다. 만약 다를 경우는 어떻게 될까?

2×3행렬과 3×2행렬을 곱했을 때이다. 앞서 본 예시와 별다른 차이가 없다. 이번에도 첫번째 행렬을 A, 두번째 행렬을 B, 결과 행렬을 C로 한다면 A의 행과 B의 열을 곱하는 성질때문에 결과 행렬의 경우 (A의 행의 수)×(B의 열의 수)가 된다. 따라서 A의 행의 수와 B의 열의 수가 같아야지만 행렬의 곱셈을 할 수 있다.

2. 소스 코드 구현

구현하는 데 사용한 언어는 C++이다.

#include <iostream>
using namespace std;

int main() {
	int A[2][3] = { {1, 2, 3}, {4, 5, 6} };
	int B[3][2] = { {7, 8}, {9, 10}, {11, 12} };
	int C[2][2];

	int A_col = sizeof(A[0]) / sizeof(int); 
	int A_row = sizeof(A) / sizeof(A[0]);
	int B_col = sizeof(B[0]) / sizeof(int);
	int B_row = sizeof(B) / sizeof(B[0]);

	// 행렬의 곱셈
	int sum;
	for (int r = 0; r < A_row; r++) {
		for (int c = 0; c < B_col; c++) {
			sum = 0;
			for (int k = 0; k < A_col; k++) {
				sum += A[r][k] * B[k][c];
			}
			C[r][c] = sum;
		}
	}

	// 결과 행렬 출력
	for (int r = 0; r < A_row; r++) {
		for (int c = 0; c < B_col; c++) {
			cout << C[r][c] << '\t';
		}
		cout << endl;
	}

	return 0;
}

앞서 보았던 형태처럼 A의 행의 값 x B의 열의 값 으로 계산한다. 시간 복잡도의 경우 O(N^3)이지만 다른 알고리즘을 쓰면 시간 복잡도를 더 개선할 수 있다고 한다. 이는 나중에 다뤄보겠다.

3. 참조

"행렬 곱셈", 위키피디아, https://ko.wikipedia.org/wiki/%ED%96%89%EB%A0%AC_%EA%B3%B1%EC%85%88