확률 변수는 어떠한 형태의 확률 분포(정규 분포, 균일 분포, 이항 분포, 베르누이 분포 등)를 따르고, 해당 확률 변수로부터 어떤 사건(event)을 관측할 수 있다. 확률 변수는 불확실성을 가진다. 또한 확률 변수로부터 실현된 어떤 사건(event)은 불확실성에 대한 정보를 가진다.
Entropy는 확률 변수에 대한 불확실성을 수치화 한 개념으로 이해하면 된다.
이산 확률 분포를 대상으로 글을 작성했으며, 연속 확률 변수의 경우, 을 로 치환함으로써 일반화가 가능하다.
어떤 이산 확률 분포를 따르는 확률 변수 가 존재한다고 하자. 이때 의 분포를 아래와 같이 나타낸다.
총 개의 사건이 발생 가능하며, 각각의 사건에 대한 확률은 로 표현한 것이다.
1. Shannon Information Content of single event
Shannon Information content는 확률 변수로부터 실현된 하나의 사건 가 가지는 정보량을 수치화 한 것이다.
공식은 아래와 같다.
발생 가능성이 높은 사건의 발생은 적은 정보량을 가지고, 반대로 발생 가능성이 희박한 사건의 발생은 높은 정보량을 가진다는 직관으로 이해할 수 있다. 이 때, shannon information content의 단위는 bit이다.
2. Entropy of the Random Variable
확률 변수 의 엔트로피는 해당 확률 변수의 불확실성으로 이해할 수 있다.
Entropy는 shannon information content의 기댓값(expectation)이다. 즉, 아래와 같이 구해진다
이렇게 정의된 엔트로피는 아래와 같은 성질을 갖는다.
확률분포가 결정론적일 때, 엔트로피는 0이 되고, 확률분포가 균일분포일 때, 엔트로피는 최대가 된다. (Jensen’s Inequality로 증명 가능).
직관적으로 이해하자면, 확률분포가 결정론적이면 즉, 언제나 같은 사건이 발생한다면 불확실성이 낮으니(없으니) 엔트로피가 0이고, 확률분포가 균일 분포이면, 어떤 사건이 발생할 지 종잡을 수 없으므로 엔트로피가 높다고 이해하면 된다.
어떤 이산 확률 분포가 주어졌을 때, 해당 분포의 엔트로피는 아래의 python 코드를 통해서 구해볼 수 있다.
3. Joint Entropy
Joint Entropy도 Entropy와 거의 유사한 개념이다. 다만 확률 변수가 두 개 이상인 joint distribution에 대해 entropy를 계산할 뿐이다. 두 개의 확률변수에 대한 joint entropy 공식은 아래와 같다.
Joint Entropy의 경우, 확률 변수들이 독립이면 각각의 확률 변수들의 엔트로피의 합과 일치한다. 즉,
and are independent
4. Cross Entropy
Cross Entropy는 딥러닝에 사용되는 손실함수에서 등장하는 개념이다. 쉽게 말하면, 같은 정의역(domain)을 갖는 두 확률 분포 간의 유사도 라고 이해하면 된다. classification에서 사용되는 cross entropy loss도 마찬가지다. 어떤 이미지가 주어졌을 때, 모델이 예측한 해당 이미지의 class의 분포 와, 원 핫 인코딩 된 실제 class의 분포 사이의 cross entropy를 최소화하는 것이 cross entropy loss의 역할이다.
두 분포 와 가 있을 때, 두 분포간의 cross entropy는 아래 수식을 통해 구할 수 있다.
Cross Entropy는 몇 가지 성질들을 가진다.
- , P=Q일 때 등식이 성립
위 2 은 Gibb's Inequality를 통해 증명할 수 있다.
5. KL-Divergence
KL-Divergence 또한 같은 공간상에서 정의되는 두 확률 분포 사이의 다른 정도를 수치화하는 데 사용된다. 이는 아래 공식과 같이 정의된다.
cross entropy와 유사한 개념이나 공식은 조금 다르다. 하지만 앞서 언급했듯, 이므로, 머신러닝의 관점에서 분포 를 최적화 한다고 했을 때(분포 와 유사해지도록), cross entropy를 최소화하는 것과 KL-Divergence를 최소화하는 것은 동일하다.
KL-Divergence 또한 기억해야 할 몇 가지 특징들이 있다.
- - Gibb's Inequality, P=Q 일 때, 등호가 성립
첨언하자면, KL-Divergence의 경우 두 분포 사이의 거리를 의미한다고 해석되므로, 이것이 하나의 metric(distance measure)처럼 보일 수도 있지만, KL-Divergence는 metric이 아니다. metric의 조건인 transitivity를 만족하지 않기 때문이다.
5.5. Jensen's Inequality, Gibb's Inequality
위에서 Jensen's Inequality와 Gibb's Inequality와 같은 부등식들이 등장했는데, 이 부분에 대해서 잠시 설명을 하자면,
- Jensen's Inequality
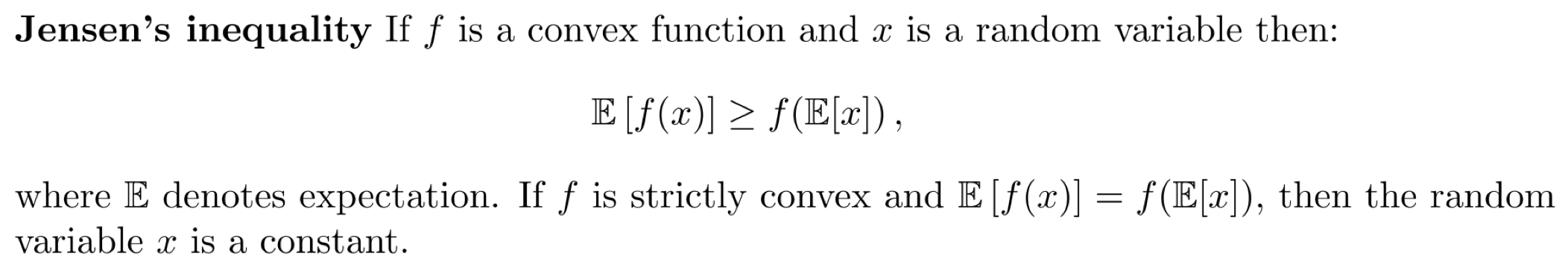 즉, 함수 f가 convex일 때, f(X)의 기댓값이, X의 기댓값에 f를 취한 것보다 크거나 같다는 것이다. 증명 과정은 아래와 같다.
즉, 함수 f가 convex일 때, f(X)의 기댓값이, X의 기댓값에 f를 취한 것보다 크거나 같다는 것이다. 증명 과정은 아래와 같다.

- Gibb's Inequality
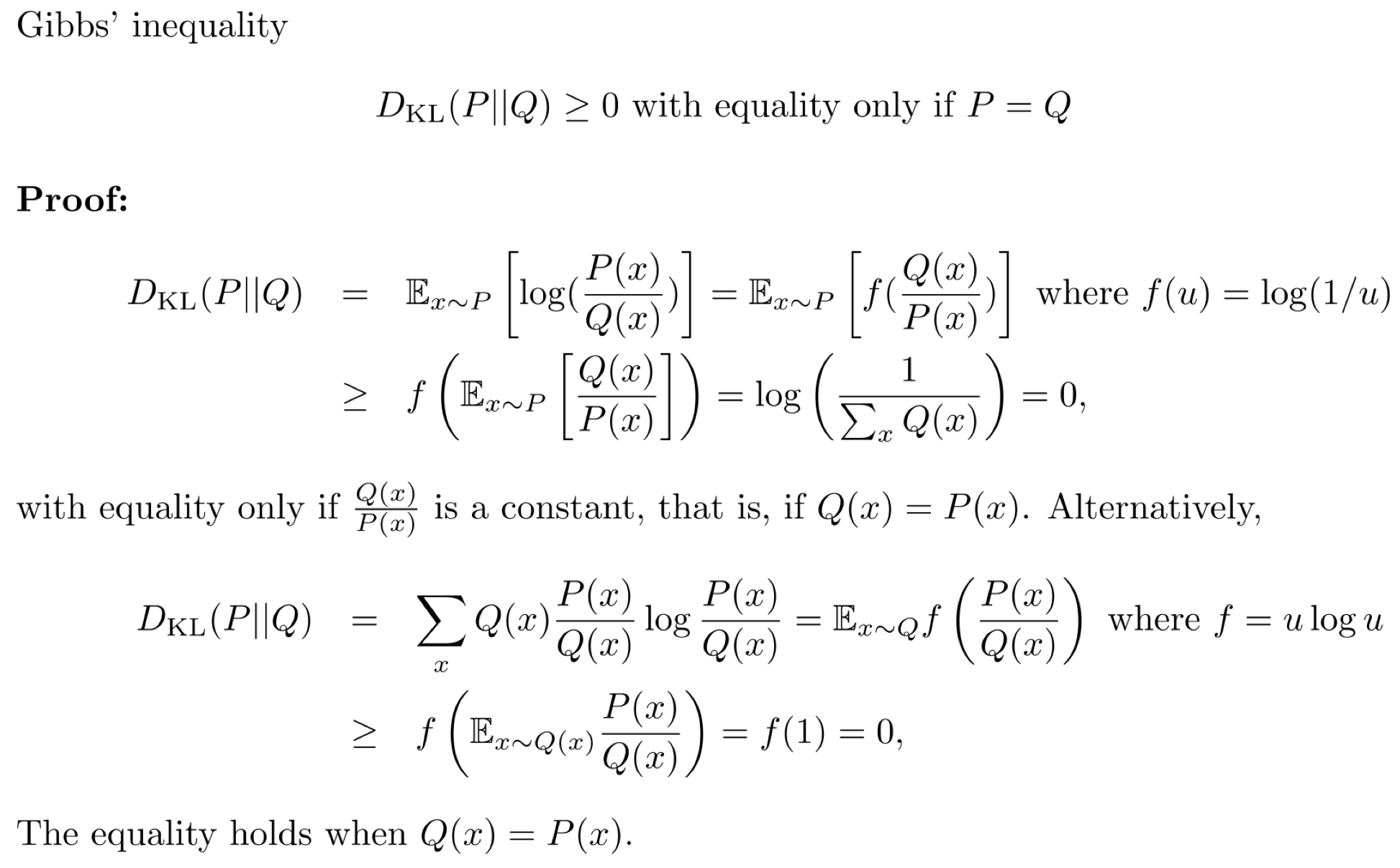 즉, KL Divergence는 항상 0보다 크거나 같다는 것이다.
즉, KL Divergence는 항상 0보다 크거나 같다는 것이다.
