ML/DL Basics

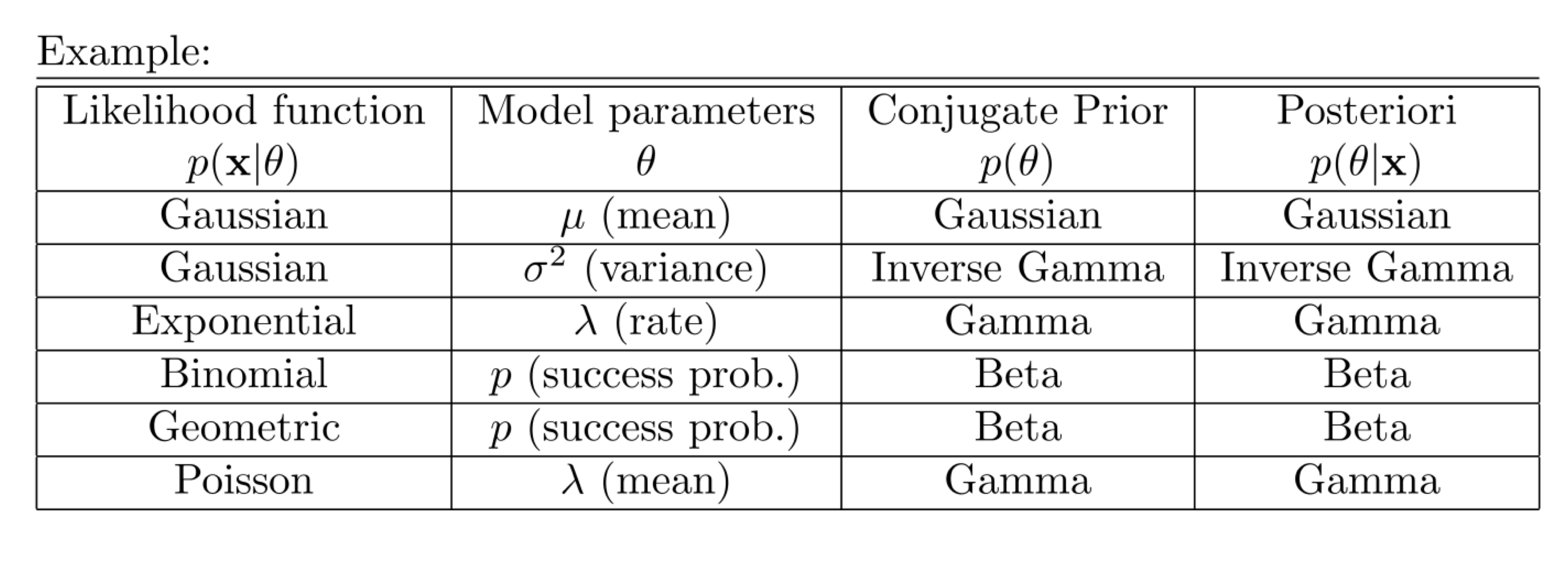
bayesian estimation은 어떠한 모수(Parameter)가 unknown constant가 아닌, 어떠한 확률 분포를 가지는 확률 변수라고 가정한다. 이러한 가정을 바탕으로 데이터 $\\mathbf{x}$가 주어졌을 때, 모수 $\\theta$의 확률 분포

확률 변수는 어떠한 형태의 확률 분포(정규 분포, 균일 분포, 이항 분포, 베르누이 분포 등)를 따르고, 해당 확률 변수로부터 어떤 사건(event)을 관측할 수 있다. 확률 변수는 불확실성을 가진다. 또한 확률 변수로부터 실현된 어떤 사건(event)은 불확실성에

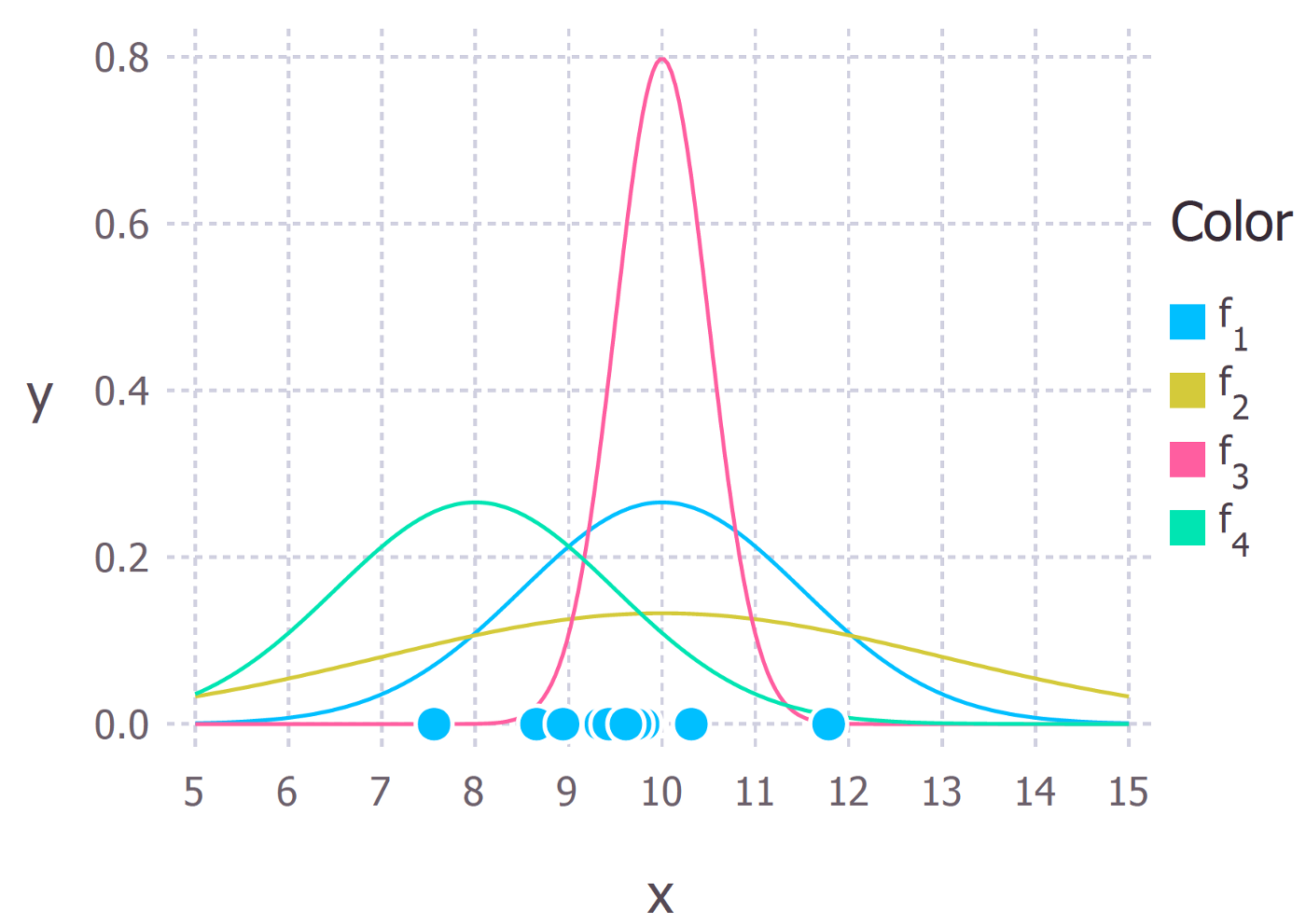
maximum likelihood estimation은 빈도주의 통계학에서 파라미터를 점추정할 때 흔히 사용하는 방법입니다.추정의 대상이 되는 파라미터는 특정 분포의 파라미터일수도 있고, 어떤 모델의 파라미터일 수도 있습니다. 이번 포스팅에서는, 모델의 파라미터를 추정