[GRL Book 5.2] Aggregation Functions

GNN의 한 레이어는 두 스텝으로 구성됩니다.

1. 주변 노드들의 정보를 aggregate하여 message를 생성하는 aggregation step
2. message와 노드의 현재 임베딩을 취합하여 노드의 임베딩을 업데이트하는 updating step

본 포스트에서는 1번에 해당하는 aggregation의 다양한 방법론에 대해 설명해 보겠습니다.

1. Neighborhood Normalization

Node degree

앞서 기본적인 Neural massage passing 구조에 대해 다루었습니다. 수식으로 아래와 같이 표현될 수 있습니다.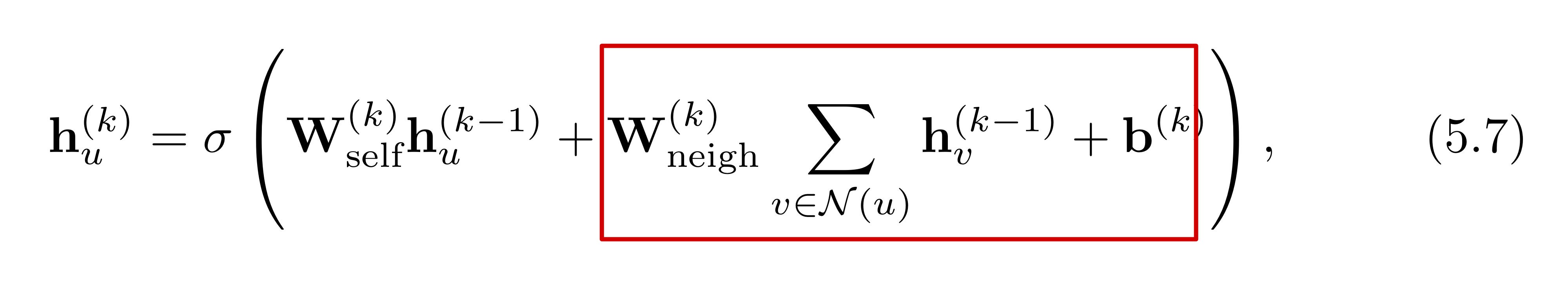네모로 표시된 부분을 보면, 이웃 노드들의 임베딩을 aggregate하는 것에 있어 단순 합을 수행합니다. 하지만 만약 특정 노드의 node degree(다른 노드와 연결된 간선(edge)의 수)가 매우 높다면, aggregation을 수행하는 과정에서 numerical instability가 생길 수도 있고, 최적화에 어려움이 생길 수도 있습니다.

따라서, aggregation과정에서 normalization을 수행할 필요가 있습니다. 이웃 노드들의 단순 합을 해당 노드의 node degree로 나누어 주는 것이죠. 다음과 같이 표기할 수 있습니다.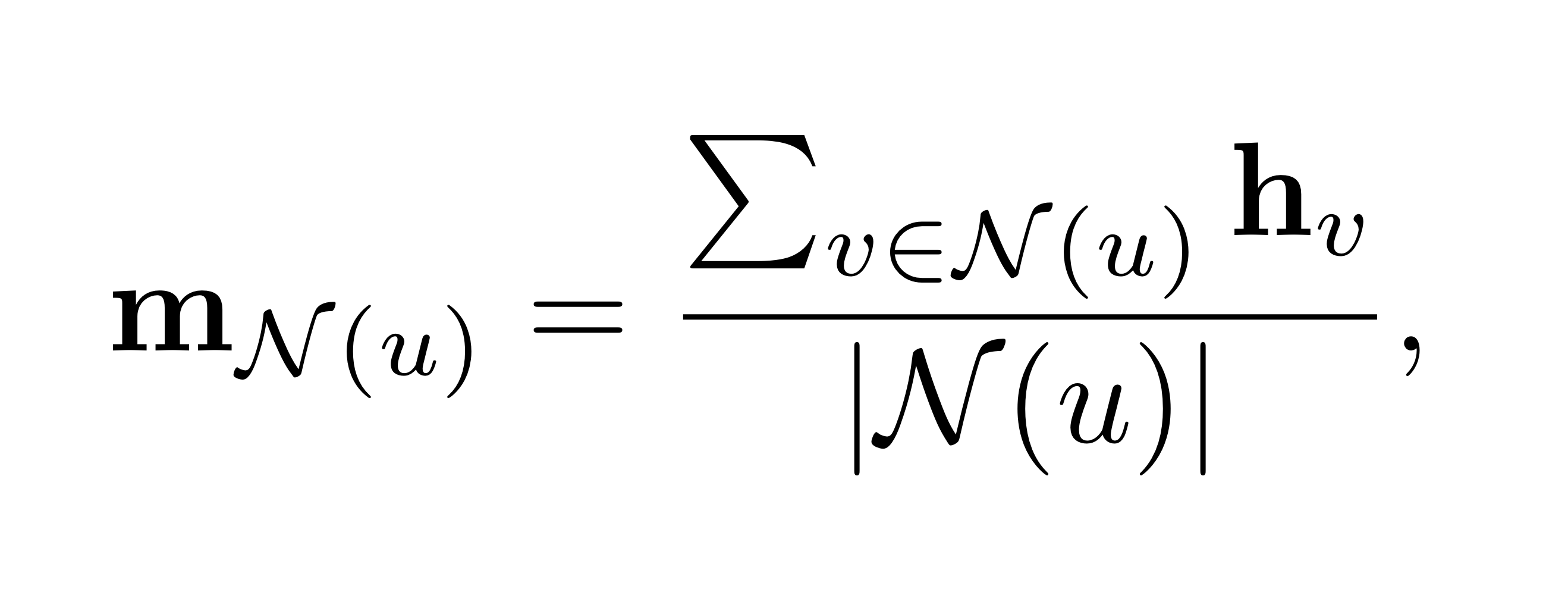혹은, symmetric normalization을 적용하여, 아래와 같이 noramlization을 수행할 수도 있습니다. 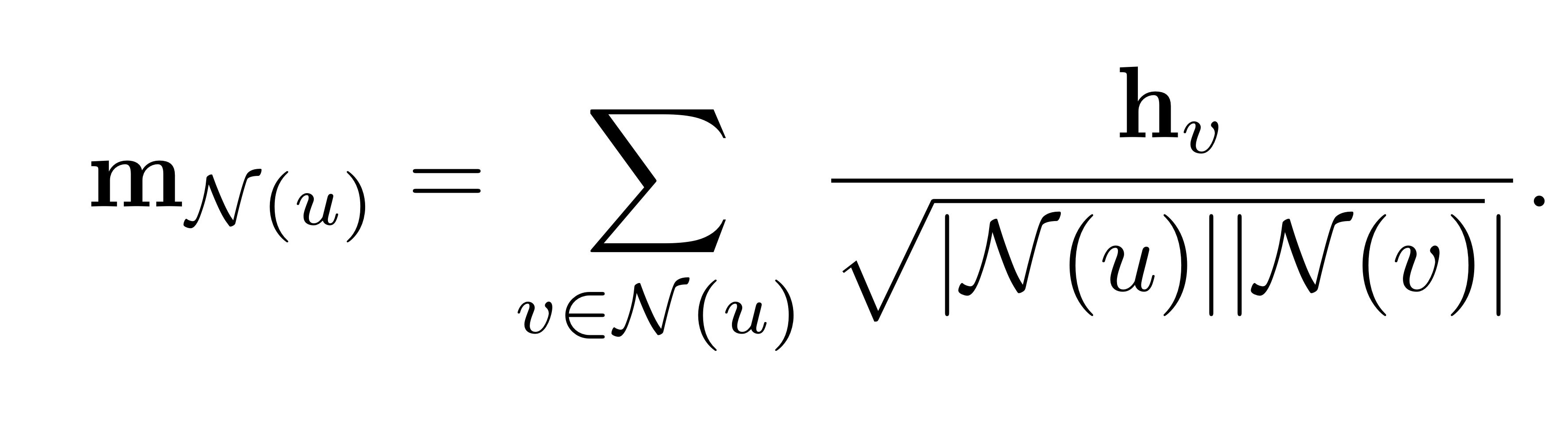위와 같이 symmetric normalization을 통해 aggregation을 수행하는 방식이 Graph Convolution Network(GCN)입니다.

Graph Convolution Network

GCN의 $k^{th}$ layer 연산은 아래와 같이 표현할 수 있습니다.(self loop적용)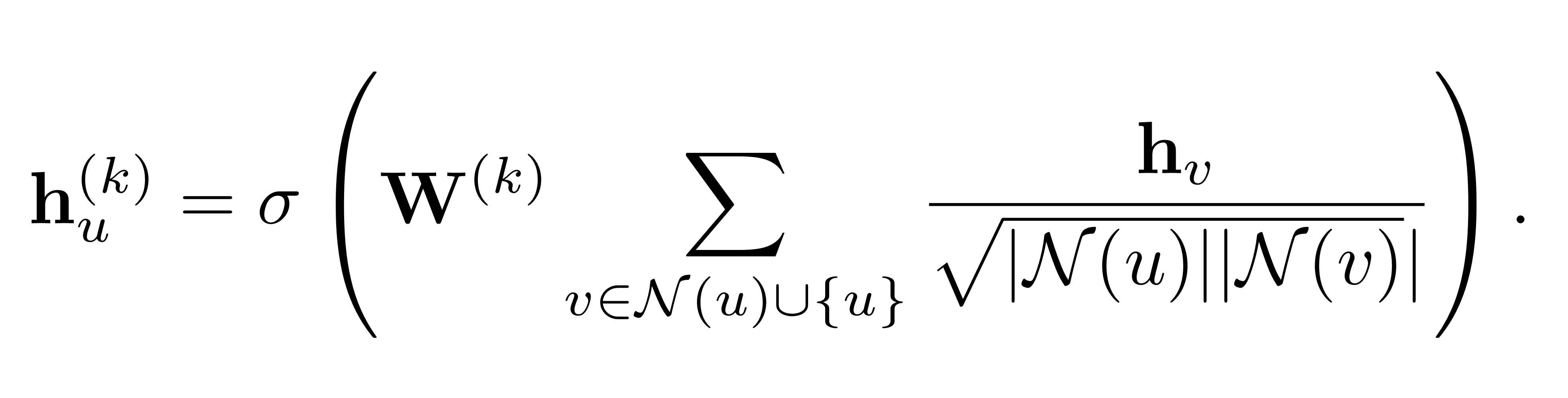위와 같은 노드 단위의 연산을 행렬 연산으로도 다음과 같이 표기할 수 있습니다.
$\mathbf{H}^{(k)} = \sigma[\mathbf{D}^{-{1\over 2}}\cdot(\mathbf{A}+\mathbf{I}) \cdot \mathbf{H}^{(k-1)}\cdot\mathbf{D}^{-{1\over 2}}\cdot \mathbf{W}^{(k)}]$

여기서,
$\mathbf{A}$ : adjacency matrix
$\mathbf{D}$ : diagonal degree matrix where $D_{u,u} = |\mathcal{N}(u)|$
$\sigma$ : activation function(ReLU, tanh등)
입니다.

2. Set aggregation

node degree를 사용하여 node aggregation시 normalization을 해 주는 것도 좋은 방법이지만, 조금 더 복잡한 모델링을 위해서는 node degree를 고려하는 것 외에도 encoder구조 자체를 개선할 필요가 있습니다.

특정 노드의 이웃 노드들 간에는 정해진 순서가 없습니다. 따라서, Neighborhood aggregation operation은 permutation invariant해야 합니다. 따라서 단순히 이웃 노드들의 임베딩을 이어붙인 후(concatenate) MLP를 적용하는 방식은 적절하지 않습니다.

가장 기본적인 aggregation operation은 이웃 노드의 임베딩에 대해 단순 합을 하는 것입니다. 하지만, 이것 말고도 다양한 방법들이 있습니다.

Set pooling

첫 번째 방법은 기존의 sum aggregation 방식(GCN)을 일반화하는 것입니다. 수식으로는 아래와 같이 표현할 수 있습니다.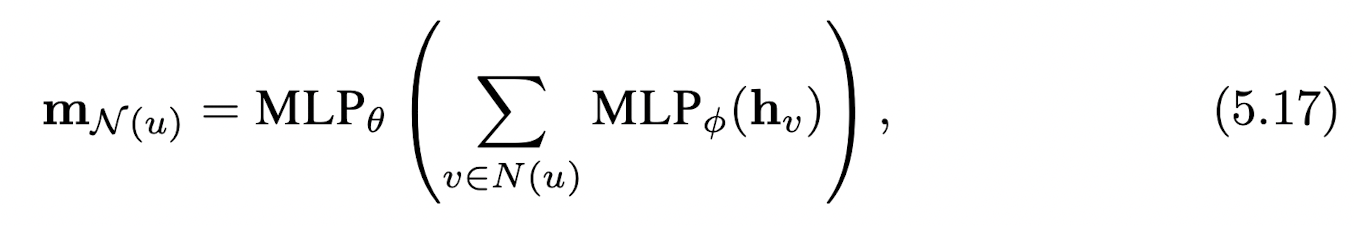 여기서 $\phi$와 $\theta$는 학습 가능한 파라미터입니다. 단순히 주변 노드 임베딩에 대한 summation을 하는 대신, 주변 노드 임베딩에 대해 MLP를 취해 준 뒤에 summation을 수행하고 다시 여기에 대해 MLP를 취해 줌으로써 조금 더 expressive한 message $\mathbf{m}_{\mathcal{N}(u)}$를 얻을 수 있습니다.

$\mathbf{MLP}_{\phi}(\cdot)$에 대해 summation $\sum$ 말고도 다양한 permutation invariant operation(ex. Maxpooling, Average Pooling)을 적용할 수 있으며, 앞서 다루었던 normalization을 적용할 수도 있습니다.

Janossy pooling

Janossy pooling은 LSTM과 같은 permutation sensitive operation을 사용하여 주변 노드 임베딩을 aggregate한다는 점에서 위에서 설명한 set pooling과 다릅니다.

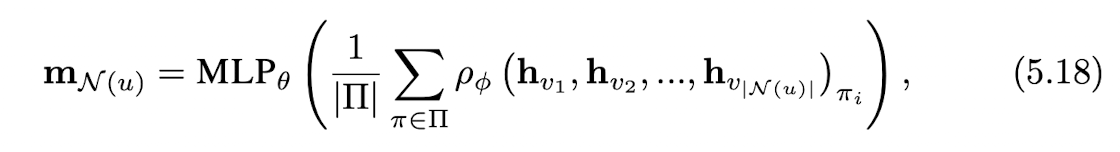해당 수식에서 $\rho_{\phi}(\cdot)$은 LSTM과 같은 permutation sensitive operator를 의미합니다. 이 경우엔, 여러 번$(= |\prod|)$의 permutation sampling을 통해 $\rho_{\phi}(\cdot)$를 여러번 계산한 후에, 평균값을 취함으로써 이웃 노드의 임베딩을 aggregate합니다.
Murphy et al.[2018]

3. Neighborhood Attention

Graph Attention Network(GAT)

aggregation function을 개선하는 또 다른 방법은 바로 어텐션 메커니즘을 사용하는 것입니다. 즉 이웃 노드들을 공평하게 취합하여 message를 aggregate 하는 것이 아니라, 학습 가능한 가중 합을 하는 것입니다.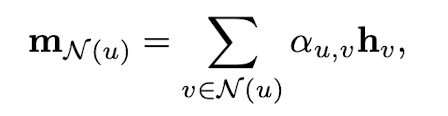 그리고, $\alpha_{u,v}$는 아래와 같이 정의됩니다.($\mathbf{a}, \mathbf{W}$는 trainable parameters) 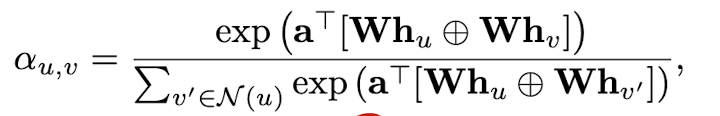혹은, 아래와 같은 variants들을 통해 attention weight를 정의할 수도 있습니다.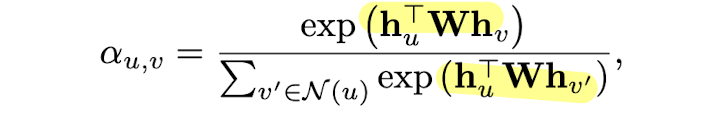

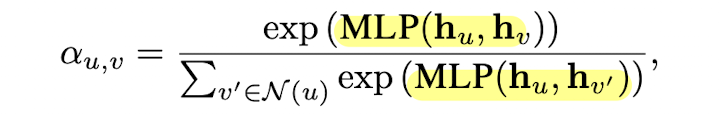
Relation to Multihead Attention

위와 같이 attention head를 하나로 구성할 수도 있지만, attention head를 여러 개로 구성할 수도 있습니다. 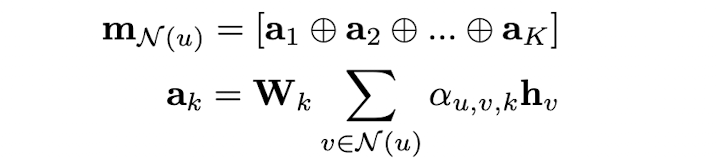위와 같이 $K$개의 attention parameter를 설정하고, 각 head에 대해서 aggregated message인 $\mathbf{a}_k$를 뽑은 후에, $\mathbf{a}_1 ...\mathbf{a}_K$를 concatenate하여 message $\mathbf{m}_{\mathcal{N}(u)}$를 정의할 수도 있습니다. 이 경우, 만약 모든 노드들이 연결되어 있다면 NLP에서의 multihead attention transformer와 같아집니다.(token이 노드, token간의 연결관계를 간선에 비유)

따라서, multihead attention이 적용된 GNN을 구현할 때, transformer에 attention mask(=adjacency matrix)를 적용한다는 관점에서 접근하는 것도 가능합니다.