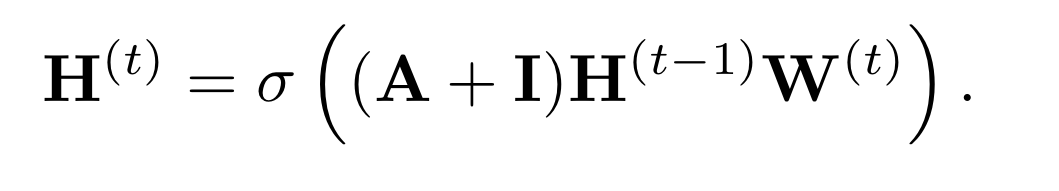[GRL Book 5.1] Basic Neural Message Passing Framework

오늘은 가장 기본적인 Graph Neural Network의 프레임워크인 neural message passing에 대해 소개하겠습니다.

node2vec이나 DeepWalk와 같은 방식으로, 각 노드에 상응하는 임베딩(shallow embedding)을 학습할 수도 있지만 조금 더 복잡한 encoder구조에 대해 다루어 보려고 합니다.

Intuitions

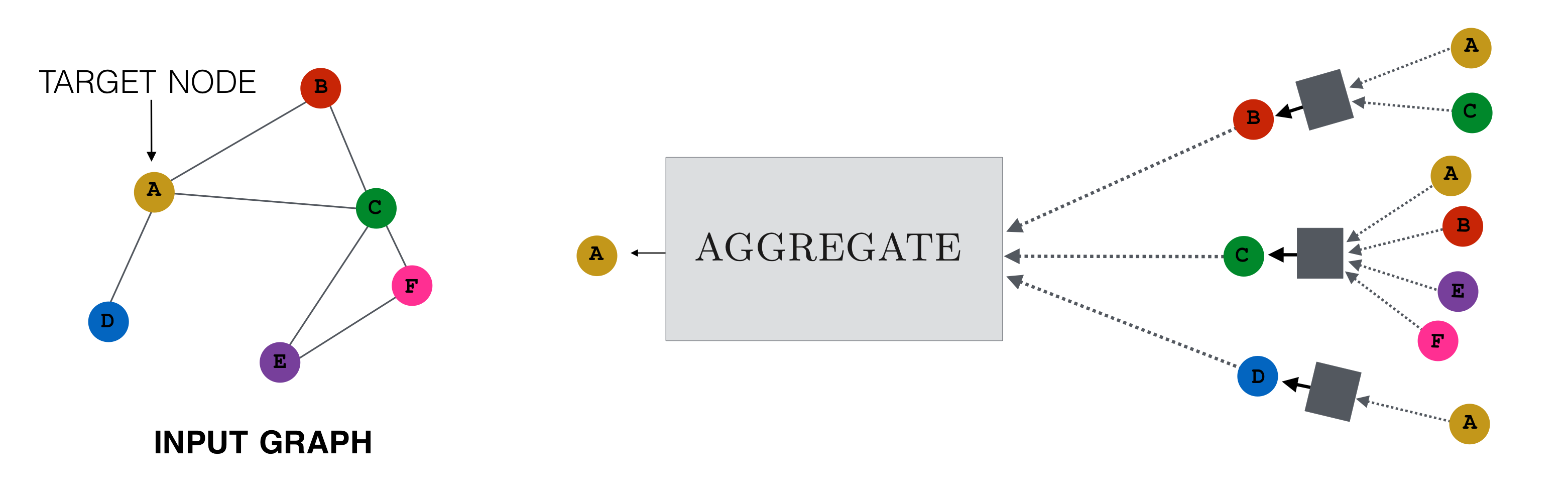Input Graph에서 노드A 에 대한 임베딩을 학습하려고 합니다. 기존의 node2vec의 접근에서는 각 노드에 대한 unique한 embedding을 학습했으나, neural message passing에서는 주변 노드들의 정보를 취합(aggregate)하여 message를 만들고, 이것을 바탕으로 해당 노드를 update하는 함수들을 학습합니다.

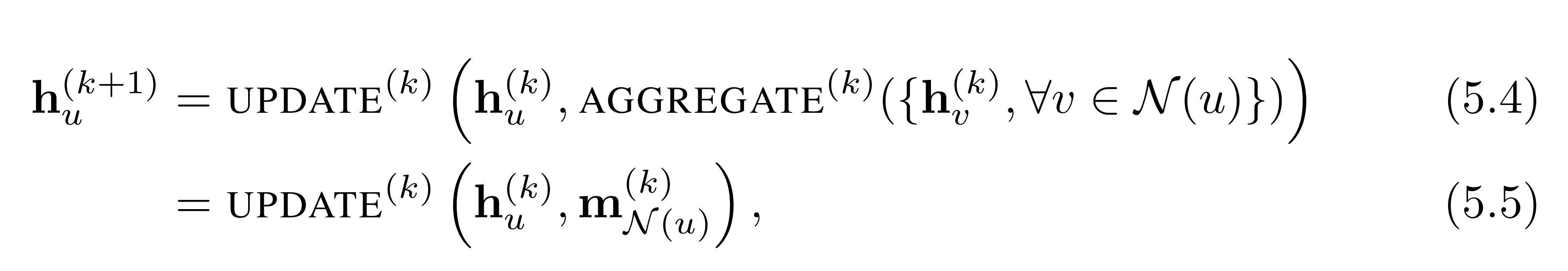
• $\mathbf{h}_u^{(k)}$ : k번째 update에서 노드 u의 임베딩
• $\mathcal{N}(u)$ : 노드 u의 이웃 노드들의 집합

여기서 $k = 1...T$ 까지 노드 임베딩에 대한 업데이트가 이루어지며, 여기서 $T$를 해당 graph neural network의 layer의 수라고 이해하시면 됩니다. 그리고 초기의 노드 임베딩 $\mathbf{h}_u^{(0)}$ 은 노드 u의 node feature로 설정합니다.

GNN의 layer의 개수가 가지는 의미에 대해서 간략하게 설명하자면,

$k = 1$이면, 노드 $u$는 해당 노드의 1-hop neighborhood인 $\mathcal{N}(u)$의 정보만 aggregate함
$k = 2$이면, 노드 $u$는 해당 노드의 2-hop neighborhood($\mathcal{N}(u)$에 속하는 노드들의 이웃노드까지)의 정보도 aggregate함
.
.
.
$k = K$이면, 노드 $u$는 해당 노드의 $K$-hop neighborhood의 정보까지 aggregate함

즉, layer가 많아질수록 특정 노드가 message를 전달 받는 범위(일종의 receptive field)가 넓어지는 것이죠. Convolution Neural Network와 비슷합니다. 픽셀들을 노드라고 하고 3x3 kernel을 사용한다고 하겠습니다. layer가 하나밖에 없으면 3x3 pixel grid로 이루어진 local node에 대한 정보만 aggregate 할 수 있습니다. 하지만 layer가 많아지면, receptive field가 넓어지게 되죠.

Formulation

Neural Message passing은 Aggregation function과 Update function으로 구성됩니다.
가장 기본적인 형태는 아래와 같습니다.

• $\mathbf{Aggregate}^{(k)} = \mathbf{W}_{neigh}^{(k)} \cdot \sum_{v \in \mathcal{N}(u)}\mathbf{h}_v^{(k-1)}$
• $\mathbf{Update}^{(k)}(\mathbf{h}_u^{(k-1)}, \mathbf{Aggregate}(\cdot)) = \sigma(\mathbf{W}_{self}^{(k)} \cdot \mathbf{h}_u^{(k-1)} + \mathbf{Aggregate}(\cdot))$

단순히 이웃 노드 임베딩들의 합으로 aggregation을 수행한 것이고, $\sigma$는 activation function으로 ReLU나 tanh입니다. 하나의 식으로 정리하면 아래와 같습니다.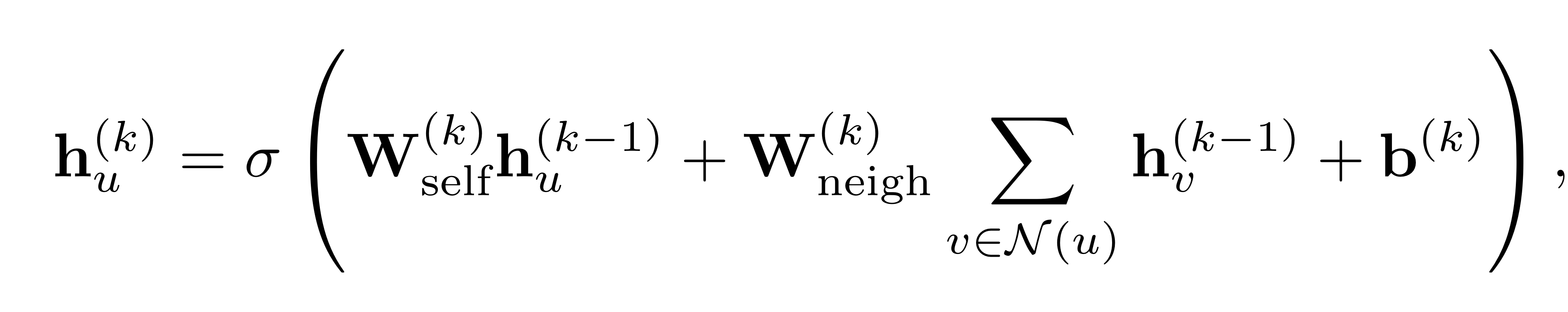 그리고, 이 연산 과정을 희소 행렬 연산(sparse matrix multiplication)으로 단순하게 표현할 수도 있습니다. 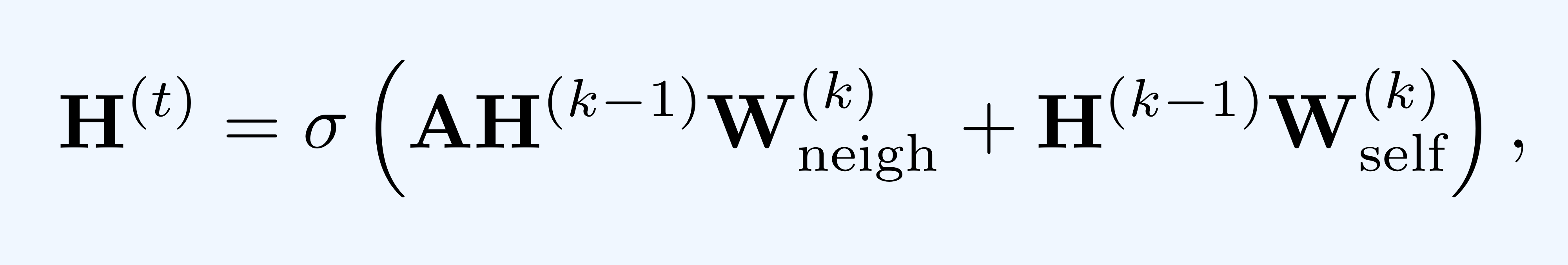이 경우, $\mathbf{A}$는 인접행렬(adjacency matrix)이고, $\mathbf{H}^{(t)}$는 $t$번째 layer에서의 각 노드 임베딩을 담고 있는 $\mathbb{R}^{|V| \times d}$차원의 행렬입니다.(notation에 오류가 있네요. 우항의 $k$를 $t$로 바꾸어야 합니다.)

Update함수 없이, Self-loop를 적용하여 더 간단하게 구현할 수도 있습니다.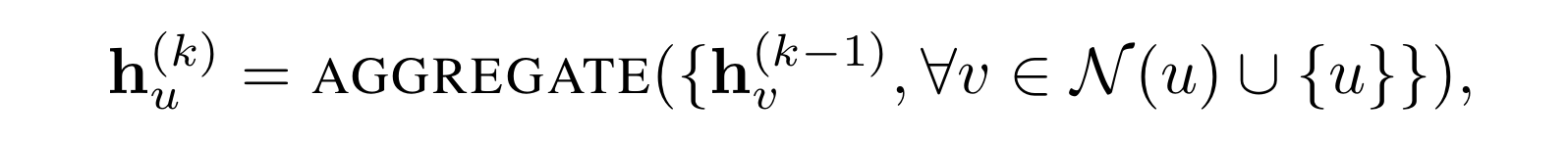 그리고 이것을 행렬 연산으로 아래와 같이 표현할 수 있습니다.