Glove(Global Word Vectors)

논문 출처 : Glove: Global Vectors for Word Representation
참고 자료 : ratsgo.github.io

Glove는 2014년 스탠포드대학교연구팀에서 개발한 단어 임베딩 방식으로 Word2Vec의 단점을 언급하며 더욱 나은 방법론을 소개하였다.

1. 기존 방법론들의 단점과 Gloved의 목적성

저자는 현재 단어 벡터를 얻는 가장 주요한 두 방법론에 대해 각각 장단점을 언급하였다. 단어-문맥 행렬(word-context Matrix)에 대한 행렬 분해(Matrix Factorization) 방식의 잠재의미분석(LSA), 그리고 Word2Vec 같은 local context window의 방식이 있다. LSA는 단어와 맥락에 관한 모든 통계 정보들을 효율적으로 잘 사용하는 반면, 단어간 비교분석(analogy) 부분에서는 매우 낮은 성능을 보였다. Word2Vec은 비교분석(analogy)에서는 뛰어난 성능을 보이지만 local한 window size 내에서만 학습을 진행하기 때문에 전체의 단어 통계 정보를 활용하지는 못하였다. 즉 각 방법론은 유사도와 전체 단어에 대한 동시발생도(co-occurrence)의 정보들을 모두 취하기는 어려웠다는 것이다.
이에 Glove는 임베딩된 두 단어벡터의 내적이 곧 두 단어의 co-occurrence 확률의 로그값이 되도록 목적함수를 설정하여 두 마리의 토끼를 모두 잡겠다는 것이 그 목적이라 할 수 있다. 즉, Method의 이름처럼 단어 벡터를 얻되 전체 통계 정보를 최대한 담겠다는 것이 그 목표이다.

2. Glove의 목적함수

시작은 $X$라는 단어-문맥 행렬을 만드는 것이다. 단어 $i$의 맥락(context)에서 단어 $j$가 몇 번 등장하였는지 그 co-occurrence 횟수가 곧 $X_{ij}$가 된다. 추가적으로 표기의 편의성을 위해 $X_i = \textstyle\sum_{k}X_{ik}$ 라고 정의한다. 그렇다면 $P_{ij} = P(j|i) = X_{ij}/X_i$ 라고 정의할 수 있다. 즉, 단어 i의 맥락(context)에서 단어 j가 등장할 확률을 의미한다.

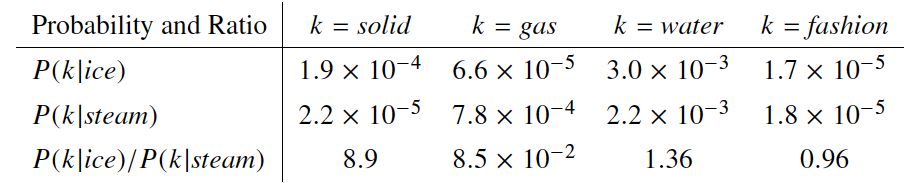
위 표를 보면 ice나 steam이라는 단어의 맥락안에 $k$라는 단어가 등장할 확률을 예시로 들고 있다. 주목해야 할 점은 두 확률 간 Ratio이다. $k$라는 단어가 두 단어와 모두 관련이 깊거나 모두 관련이 별로 없다면 이 Ratio는 1에 가까울 것이고, 둘 중 하나에만 관련이 깊다면 값이 매우 크거나 매우 작은 값이 나올 것이다. 저자는 확률 자체를 지표로 사용하는 것보다 이 Ratio를 사용하는 것이 유사도를 판단하기에 더 좋다고 판단하였다. 따라서 저자는 목적함수의 시작점을 다음과 같이 잡았다.

여기서 $w \in \reals^d$, $\tilde{w} \in \reals^d$ 는 각각 $W$와 $W'$이라는 다른 행렬에서 온 단어벡터이며 맥락단어와 타겟단어를 구별하기 위함이다. 이에 대한 자세한 설명은 뒤에서 하겠다.
Vector space는 inherently linear structure이기 때문에 Vector diffenrence로 argument를 표현하는 것이 좋다. 또, 우변이 Scalar 값이기 때문에 좌변도 Scalar값으로 표현될 수 있도록 이를 내적(inner product)로 표현한다. 여기까지 식을 변형한 과정은 다음과 같다.

타깃단어와 맥락단어는 언제든지 그 입장이 바뀔 수 있으며 이를 구분하는 것 또한 모호하다. 따라서 저자는 이를 자유롭게 바꿀수 있어야하고 이는 곧 $w \leftrightarrow \tilde{w}$ 이자 $X \leftrightarrow X^T$ 가 가능해야 한다는 것이다. $X$는 또한 Symmetry matrix이므로 $F$ 역시 이런 Symmetry 조건을 만족시키기위해 F를 $(\reals, +)$와 $(\reals_{>0}, \times)$의 groups에서 homomorphism하게 만들어야한다. 조건을 만족시키려면

이어야 하며, 이전의 식을 이용해

로 표현할 수 있다. 이것이 가능하려면 $F=exp$ 이어야하고 우리는 로그를 활용해 다음과 같이 식을 정리할 수 있다.

대칭성을 만족하려면 $\log(P_{ik})$ 와 $\log(P_{ki})$가 같아야 하는데 위 식의 $\log(X_{i})$이 걸리게 된다. 따라서 저자는 $\log(X_{i})$가 $k$에 independent하기 때문에 이를 $w_i$에 대한 bias term $b_i$로 처리하였다. 마지막으로 $\tilde{w}_ k$에 대한 bias term인 $\tilde{b}_ k$를 추가하여 다음과 같은 식을 완성하였다.

우변은 우리가 이미 알고 있는 값이며 좌변과 우변이 차이를 최소로 하는 것이 최종 목적이라고 할 수 있다. 따라서 least squares regression model을 활용하여 다음과 같은 식을 완성한다.

이때, Word2Vec의 Subsampling 기법처럼 지나치게 빈도가 높은 단어들에 대해 이에 대한 overweight를 방지하고자 $f(X_{ij})$를 정의하였다. $f$는 다음과 같은 세 가지 성질을 만족해야 한다.

1. $f(0)=0$
2. $f$는 동시 발생(co-occurrence)빈도가 낮은 경우에 대해 overweight되지 않도록 non-decreasing이어야 한다.
3. $f$는 동시 발생 빈도가 높은 경우에 대해 상대적으로 작은 겂을 주어 overweight되지 않도록 한다.

이러한 성질을 만족하도록 $f$를 다음과 같이 수식으로 정의하였다.

저자는 $x_{max} = 100, \alpha = 3/4$ 로 하였을 때 가장 좋은 성능을 낸다고 하여 다음과 같이 값을 고정하였다. 이때 그래프는 다음과 같다.

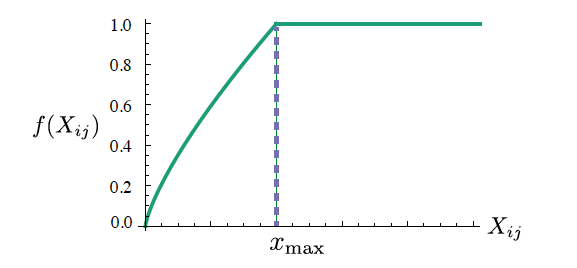
이러한 과정을 통해 최종적으로 목적함수를 최소화 하는 $W$와 $\tilde{W}$를 만들게 되고(X에 대한 matrix factorization) 이를 각각 임베딩 벡터 모음으로 사용해도 되지만 저자는 $W+\tilde{W}$를 사용하는 것이 더 좋다고 하였다.

3. 결론

같은 해 Neural Word Embedding as Implicit Matrix Factorization 논문을 통해 Skip-gram 모델이 말뭉치 전체의 global 통계량인 Shifted-PMI 행렬에 대해 matrix factorization 하는 것과 동치임이 밝혀졌다. 그럼에도 불구하고 Word2Vec의 단점을 극복하려 했다는 시도자체와 matrix factorization을 활용하려 했다는 점에서는 주목할 만 하다. 그러나 계산 복잡성이 큰 것은 matrix factorization의 고질병이다.