Word2Vec

논문출처 : Efficient Estimation of Word Representations in Vector Space / Distributed Representations of Words and Phrases and their Compositionality
참고자료 : ratsgo.github.io

Word2Vec은 2013년 구글의 Tomas Mikolov가 발표한 단어 임베딩 기법으로, 이전 글에서 다뤘던 신경망을 통한 단어의 분산표현(Distributed Representation) 학습을 바탕으로 한다. 기법 이름처럼, 그리고 우리가 아는 것 처럼 단어를 벡터로 표현하는 개념과 장점은 이전 글인 NPLM에서 소개한 바 있다. 그러나 NPLM의 분산표현 학습을 위해 Projection layer, Hidden layer 등 너무 많은 파라미터들의 계산이 필요하기 때문에 이 문제를 해결한 것이 바로 Word2Vec이라고 할 수 있다.

두 논문은 한 달의 간격을 두고 발표되었는데, 9월에 발표된 Efficient Estimation of Word Representations in Vector Space는 Word2Vec의 두 가지 방법론(CBOW, Skip-gram)에 대한 소개가 주를 이루고 있고, 10월에 발표된 Distributed Representations of Words and Phrases and their Compositionality는 두 방법 중 Skip-gram이 더 낫다고 이 전 논문에서 결론을 내린 바, Skip-gram의 성능을 개선하기 위한 3가지 최적화 방법론(Hierarchical Softmax, Negative Sampling, Subsampling)이 담겨있다.

먼저 새롭게 고안된 두 가지 모델을 소개할 예정이다. 저자는 단어의 분산 표현 학습에서 계산복잡도에 가장 크게 영향을 끼치는 것은 non-linear hidden layer이며, 이것이 우리가 신경망을 쓰는 이유이지만 더 Simpler한 모델이 필요하다고 말하고 있다. 신경망만큼 정확하지는 못해도 더 많은 데이터를 효율적으로 학습하는 모델이 저자의 목표라고 한다.

1. CBOW (Continuous Bag-of-Words) Model

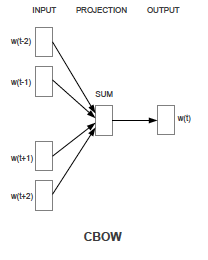
CBOW모델은 Context words로부터 Target word를 추론하는 목적의 모델이다. 이 Context의 사이즈는 임의로 지정할 수 있는데, 타겟단어의 앞(history) 과 뒤(future) 의 단어들을 동일한 개수만큼 input으로 넣게 된다. 그림에선 타겟단어 앞 뒤 단어를 2개씩 context words로 사용하였다.

각 단어는 one-hot vector 형태의 $w(t)\in\Reals^{1\times V}$ 로 표현되고, Vocabularly size를 $V$, Projection layer의 노드 개수를 $N$이라고 했을 때 Input layer 와Projection layer 사이의 가중치 행렬인 $W\in\Reals^{V \times N}$ 가 각 context word와 곱해지고(이전처럼 w(t)가 one-hot vector이기 때문에 원소가 1인 index의 해당 행벡터를 참조(look-up)하는 것 뿐이다), 이들을 모두 더해 평균낸 벡터 $H\in\Reals^{1\times N}$가 그 결과물이 된다. 이 벡터 $H$는 Projection layer와 Output layer사이의, $W$과 전치(Transpose)된 형상의 가중치 행렬 $W'\in\Reals^{N \times V}$과의 곱을 통해 최종 추론 결과 벡터인 $O\in\Reals^{1\times V}$가 된다. (참고로 $W$와 $W'$은 그 형상만 전치된 형태이지 $W^{T} = W'$의 관계가 성립하지 않는다.) Output vector $O$는 softmax를 통해 정규화된 확률값으로 변환된다. 학습과정에서는 이를 Cross Entropy error를 통해 정답레이블과 비교하여 역전파(Backpropagation) 방법으로 학습하게 된다. 학습을 마친 $W$는 각 단어의 분산 표현으로 사용할 수 있다.

CBOW모델의 특징은 순서를 신경쓰지 않는다는 점이다. History words와 Future words의 order가 학습시에 고려되지 않기 때문이다. 그렇기 때문에 Bag-of-words라는 이름이 붙는 것이다. $n$을 context의 size라고 할 때, 이 모델의 Training Complexity Q는 다음과 같다.

마지막에 $\log_2 (V)$ 가 되는 것은 연산량을 줄이기 위해 softmax 대신 Hierarchical Softmax를 사용했기 때문이다(추후 설명).

2. Skip-gram model

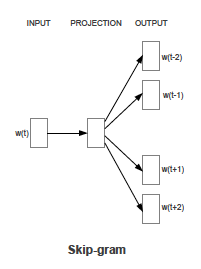
Skip-gram 모델은 CBOW 모델과 반대로 Target 단어로 부터 그 주변 Context 단어들을 예측하는 모델이다. Context의 크기인 Window 사이즈를 정해놓고, 그만큼 추측한다고 보면 된다. 그림에선 $w(t)$에 대해 앞뒤로 2개씩의 단어를 추론하는 것을 보여주고 있다.

Input으로 들어가는 Target 단어는 $w(t)\in\Reals^{1\times V}$ 형태의 one-hot vector로 Input layer 와Projection layer 사이의 가중치 행렬인 $W\in\Reals^{V \times N}$ 과 곱해진다. 그 결과물인 $H\in\Reals^{1\times N}$ 가 Projection layer와 Output layer사이의, $W$과 전치(Transpose)된 형상의 가중치 행렬 $W'\in\Reals^{N \times V}$과의 곱을 통해 최종 추론 결과 벡터인 $O\in\Reals^{1\times V}$가 된다.

$C$를 context의 size라고 할 때, 이 모델의 Training Complexity Q는 다음과 같다.

Skip-gram model의 특징이자 학습에 있어 장점인 것은 한 Target 단어에 대해 여러번 학습을 진행한 다는 것이다. 그림을 예시로 들면, 한 Target 단어에 대해 총 4개의 context 단어들을 추론해야 하는데, 이를 한번에 하는 것이 아닌 Target 단어와 context 단어들 중 하나씩 쌍을 맺어 추론한다는 뜻이다. 이때 이 방법을 좀 더 최적화 하기 위해 위에서 언급한 Negative Sampling 과 Subsampling 이 등장한다.

(1) Negative Sampling

서동건은 오늘 여자친구와 식당에 가서 마라탕을 먹었다.

예시를 드는 것이 이해하기 쉬울 것 같다. 식당에 라는 타겟단어를 주고 오늘, 여자친구와, 가서, 마라탕을 이라는 맥락단어를 추론해내야 한다. 이때 앞에서 언급한대로 (식당에, 오늘), (식당에, 여자친구와) ... 의 순서쌍을 만들게 되는데, 이렇게 맥락에 실제로 등장한 단어들과 타겟단어들을 쌍 맺은 것을 Positive Sample이라고 한다. 반면, 맥락에 등장하지 않은 단어와 쌍을 맺은 것을 Negative Sample이라고 한다. 예를 들면 (식당에, 책상), (식당에, 민수는) 등이 될 수 있을 것이다. 이렇게 한다면 한 corpus(말뭉치) 에 대해서 많은 학습 데이터 쌍을 만들어 낼 수 있다.

$c$를 window size라고 하고 $T$를 Sequence length라고 한다면, Basic한 Skip-gram 모델의 목적함수는 다음과 같다.

이때 $p(w_o|w_t)$ 형태의 조건부 확률은($w_o$는 맥락 단어)

식의 일반적인 Softmax의 방법으로 구해지는데, 모든 단어와 Target 단어의 내적 후 exp를 취하는 것은 많은 계산량을 요구한다. 따라서 모든 단어가 아닌 일부 단어만 뽑아서 계산을 하게 된다. 이때 등장하는 것이 Negative Sample이다. $k$라는 하이퍼파라미터를 지정하여 한개의 Positive Sample마다 $k$개의 Negative Sample을 같이 학습하는 과정인 것이다. 이때 k의 값에 대하여, 작은 데이터셋에 대해서는 k를 5~20, 큰 데이터셋에 대해서는 k를 2~5로 지정하는 것이 좋다고 하였다. 저자는 말뭉치에 등장하지 않는 희귀한 단어가 Negative Sample에 조금 더 잘 뽑히도록 다음과 같이 그 확률을 정의하였다.

$U(w_{i})$는 유니그램 확률로 (해당 단어 빈도/전체 단어 수)를 의미한다.

이러한 확률을 통해 $p(w_o|w_t)$ 을 매번 Softmax로 구하는 것이 아닌 다음과 같은 식으로 대체하게 된다.

해당 타겟단어와 맥락단어가 Positive Sample(+) 일 확률과 Negative Sample(-) 일 확률은 시그모이드 함수를 통해 위와 같이 표현하였다. 이런 방식을 Binary Classification이라고 한다. Positive Sample의 경우 두 벡터의 내적을 최대화 하는 것은 곧 cosine similarity를 최대화하는 것과 같다. 즉 타겟 단어와 맥락 단어의 연관성을 높이는 과정인 것이다. Negative Sample의 경우 그 반대라고 생각하면 된다. 또한 $v_{w_o}^{\prime}$는 $W'$에서 참조한 벡터이고, $v_{w_t}$는 $W$에서 참조한 벡터이다. $p(w_o|w_t)$을 최대화 시키면 Skip-gram의 목적함수 역시 최대화 되는 것과 같다.

(2) SubSampling

SubSampling의 목적은 조사 같은 자주 등장하는 단어에 대해 학습에서 아예 제외시키는 기법이다. $f(w_i)$를 단어 $w_i$의 빈도라고 할 때, 해당 단어가 학습에서 제외될 확률은 다음과 같다.

저자는 $t$의 값을 $10^{-5}$로 설정하였다. 학습 전 위의 $P_{negative}(w_i)$과 더불어 학습 전에 일괄적으로 미리 계산되어 학습시에 사용하는 수치이다.

(3) Hierarchical Softmax

사실 Negative Sampling을 통해 대체된 기법이나, 저자가 발표한 첫 번째 논문에서는 CBOW와 Skip-gram에서 Hierarchical Softmax을 사용하여 마지막 $p(w_o|w_t)$의 계산량을 줄이려고 하는 Negative Sampling과 같은 목적을 가지고 있었다. 성능은 Negative Sampling이 앞선다. 구체적인 내용은 Hierarchical Probabilistic Neural Network Language Model 논문을 참고하길 추천한다. 여기선 저자의 논문에 기재된 설명을 요약해서 서술하겠다.

모든 $W$개의 단어들을 binary tree representation으로 나타낸 후 각 노드마다 자손 노드와의 상대적 확률(relative probability)를 표현한다. 이 과정이 곧 단어의 나열에 확률을 부여하는 수단이 될 것이기 때문이다. $n(w,j)$를 root에서 $w$라는 단어로 가는 path의 $j$번째 노드라고 하고 $L(w)$를 그 path의 길이, $n$이라는 노드에 대해 임의의 자손노드 $ch(n)$, $\llbracket x \rrbracket$ 을 $x$가 참이면 1, 거짓이면 -1의 값을 가진다고 할 때, $p(w|w_t)$를 다음과 같이 정의한다.

당연히, $\textstyle\sum_{w=1}^W p(w|w_t)=1$ 이다. 저자는 Hierarchical Softmax의 Tree를 Huffman Tree를 사용했다고 한다.

3. Conclusion

여러 모델과 복잡한 내용의 최적화 기법들이 소개되었지만 결론적으로 우리에게 중요한 건 단어 임베딩 벡터이다. $W$을 사용하거나, 혹은 $W'$을 Transpose한 뒤 더해서 사용하거나, 어쩌면 두 행렬을 concatenate하여 $2\times N$ 차원의 임베딩 벡터로 사용할 수도 있다. 선택은 데이터셋과 학습 결과에 따라 다를 것이다. word2vec은 2013년에 발표되었지만 지금까지도 추론적인 방식을 통한 단어 임베딩을 구성하는데 있어 근본이 되는 모델이다.