NPLM(Natural Probabilistic Language Model)

논문 출처 : A Neural Probabilistic Language Model, 2003 Bengio et al
참고자료 : https://ratsgo.github.io/

단어를 임베딩하여 벡터로 바꾸는 과정에서 신경망기반의 기법을 제시하여 향후 Word2Vec으로 가는 기반이 된 NPLM에 대해 알아보고자 한다.

1. Curse of Dimensionality with Distributed Representations

저자는 단어를 컴퓨터에게 입력시키는 과정에서 그 차원이 커지는 것이 학습을 어렵게 만드는 근본적인 문제라고 말하고 있다. 예를 들어, 10000개의 Vocabulary size가 있고 단어를 one-hot-encoding 으로 처리한다면 해당하는 단어의 element만 1이 될 것이고 나머지는 0이 될 것이다. 이러한 벡터는 sparse vector이며 여러 측면에서 효율성이 매우 떨어지고, Vocabulary size가 매우 큰 real problem에서는 계산복잡도가 크게 늘어날 것이기 때문에 학습을 방해할 것이다. 또한 저자는 단어간의 의미적, 문법적 유사성을 표현하는 것 역시 중요하나 이런 점도 잘 이뤄지지 않고 있다고 한다. 이러한 문제점들을 극복하기 위해 고안된 것이 분산표현(Distributed Representation) 이다.

이 분산표현은 단어를 기존의 원핫벡터처럼 차원수를 Vocabulary size 전체로 하는 것이 아니라 그보다 훨씬 작은 m차원 벡터로 표현하여 sparse vector가 아닌 Dense vector 로 나타낼 수 있게 한다. 이때 element들은 discrete한 variable이 아닌 continuous한 variable인데, 저자는 Continuous variable들을 modeling 할 때가 smoothness 측면에서 discrete variable보다 훨씬 쉽고 효율적이라며 Continuous variable의 중요성을 강조하고 있다. 차원수를 줄이는 것이 주 목적이지만 element들이 Continuous variable이기 때문에 벡터간 유사도와 거리 계산이 가능하고 이는 곧 앞에서 언급한 단어의 유사성을 표현하는 것이 가능하다는 뜻이다.

2. n-gram

Statistical Language Model(통계적 언어모델) 은 이전 단어들이 주어졌을 때에 대한 다음 단어의 조건부 확률들의 곱으로 표현된다.

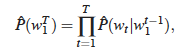
여기서 단어 순서를 고려하는 이점을 살리고 Word Sequence에서 가까운 단어들은 통계적으로 더 dependent하다는 사실을 적용, 이 방법을 개선하여 이전 n-1개만의 단어들 혹은 맥락(context)에 대한 조건부 확률을 활용하는 것이 바로 n-gram model이다.

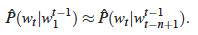
그러나, 만약 어떤 n개의 word sequence가 Training corpus(말뭉치)에 없다면 어떻게 할까? 확률을 0으로는 할 수 없을것이다. 저자는 새로운 word sequence는 얼마든지 등장할 수 있고 context가 커질 수록 더욱 이런 상황이 빈번할 것이라고 얘기한다. 이에 대한 대표적인 해결책으로 더 작은 context를 사용해 살펴보는 Back-off 방법(Katz, 1987)과, 특정한 값을 더해 확률을 0으로 만들지 않는 Smoothing 방법이 있다. 저자는 그러나, 이 n-gram 모델은 context 범위를 벗어난 단어와의 연관성을 고려하지 않으며 단어간 유사성을 고려하지 않는다고 말하고 있다.
NPLM은 n-gram모델을 본질로 하되, 이러한 단점들을 극복하기 위해 앞에서 언급한 분산표현(Distributed Representation) 을 이용하는 것이다.

3. NPLM

모델의 전체 개요는 다음과 같다.

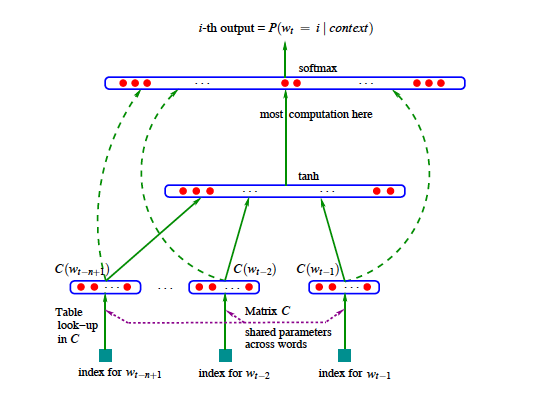
Input layer에선 n-1개의 $|V| \times 1$ 크기의 단어 one-hot-vector 인 $w_{t-n+1},\cdotp\cdotp\cdotp,w_{t-2},w_{t-1}$ 들과 이를 distributed feature vector로 바꿔주는 $m \times |V|$ 크기의 Random initialized 행렬 $C$ 을 각각 곱하여 묶어주면 input layer의 결과물인 $x$를 구할 수 있다. 아래는 단어 $w_t$와 행렬 $C$를 통해 해당하는 $x_t$를 구하는 식이다.

실제로 $w_t$는 one-hot vector이기 때문에 $C$와의 곱은 사실 $t$번째 열만 꺼내는 것과 같다. $x$를 최종적으로 표현하면 다음과 같다.

Input layer를 통해 나온 $x$가 Hidden layer와 Output layer를 거치는 연산은 다음과 같다.

$b$와 $d$는 각각 bias term이고 $H$는 hidden layer의 weights, $W$는 input layer와 output layer의 direct connection을 만들 경우의 weights를 의미한다. 이 direct connection 유무는 선택할 수 있으며 연결하지 않는다면 W를 영행렬로 만들면 된다.
이렇게 나온 $y$는 각 output 단어에 대한 unnormalized log-probabilities 이기 때문에 이를 확률로 나타내기 위해 소프트맥스 연산을 거치게 된다. 식은 다음과 같다

이 결과들을 정답테이블과 비교해 backpropagation방식으로 학습이 이루어집니다. 이때 확률적 경사하강법이 사용되고(Stochastic gradient ascent), 그 식은 다음과 같다. $\epsilon$은 학습률(learning rate)를 의미한다.

$h$는 은닉층의 유닛 개수, m은 각 단어의 feature 개수라고 할 때, 각 파라미터들의 shape를 정리하면 다음과 같다.

마무리

단어들을 $|V|$보다 작은 차원의 벡터로 표현할 수 있다는 시도 덕분에 이후 Word2vec으로 발전 할 수 있었다. 그러나 update 해야할 파라미터가 분산표현을 담당하는 $C$외에도 $H$, $U$등이 있어 여전히 계산복잡성이 높다는 것이 문제이다. 실제로 Word2Vec은 이러한 문제점을 고치기 위해 학습해야할 파라미터를 줄여냈다.