1. 트리의 개요
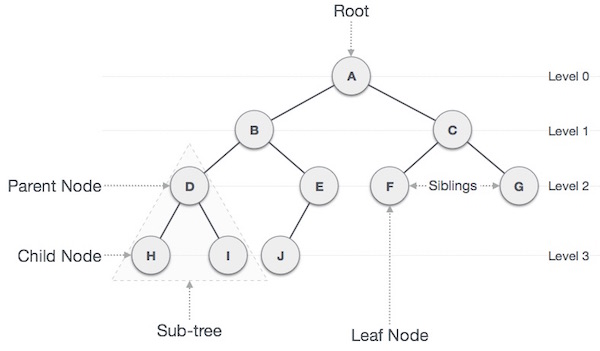
트리는 정점(Node,노드)과 선분(Branch,가지)을 이용하여 사이클을 이루지 않도록 구성한 그래프의 특수한 형태입니다.
- 트리는 하나의 기억 공간을 노드(Node)라고 하며, 노드와 노드 사이를 연결하는 선을 링크(Link)라고 합니다.
-
트리 관련 용어
-
노드 (Node)
- 트리를 구성하고 있는 기본 요소로서 자료 항목과 다른 항목에 대한 브랜치를 합친것
- 예) A, B, C, D, E, F, G, H, I, J
-
근 노드 (Root Node)
- 트리 구조에서 부모가 없는 최상위 노드
- 예) root node : A
-
디그리 (Degree)
- 각 노드에서 뻗어 나온 가지의 수
- 예) A = 2, B = 2, C = 2
-
단말 노드 (Terminal Node) = 잎 노드 (Leaf Node)
- 자식이 하나도 없는 노드, 즉 디그리가 0인 노드
- 예) H, I, J
-
자식 노드 (Son Node)
- 어떤 노드에 연결된 다음 레벨의 노드들
- 예) B의 자식 노드 : D, E
-
부모 노드 (Parent Node)
- 어떤 노드에 연결된 이전 레벨의 노드들
- 예) D, E의 부모 노드 : B
-
형제 노드 (Brother Node, Siblings)
- 동일한 부모를 갖는 노드들
- 예) F의 형제 노드 : G, D의 형제 노드 : E
-
트리의 디그리
- 노드들의 디그리 중에서 가장 많은 수
- 예) 노드 중에서 A, D, C, D, E 모두 2개의 디그리를 가지므로 앞 트리의 디그리는 2이다.
-
2. 트리의 운행법
트리를 구성하는 각 노드들을 찾아가는 방법을 운행법이라고 한다.
-
이진 트리를 운행하는 방법은 산술식의 표기법과 연관성을 갖는다.
-
이진 트리의 운행법은 세가지가 있다.
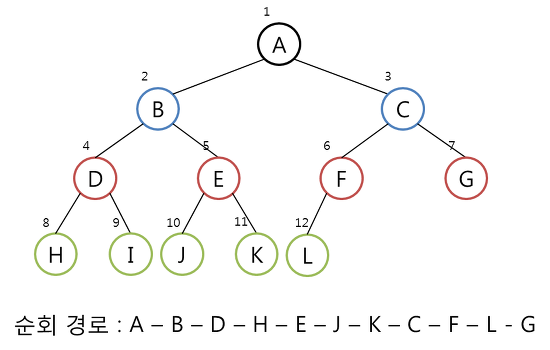
- Preorder 운행 (전위 순회)
- ROOT -> LEFT -> RIGHT 순으로 운행한다.
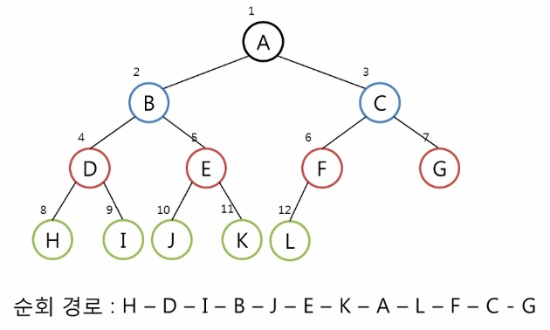
- Inorder 운행 (중위 순회)
- LEFT -> ROOT -> RIGHT 순으로 운행한다.
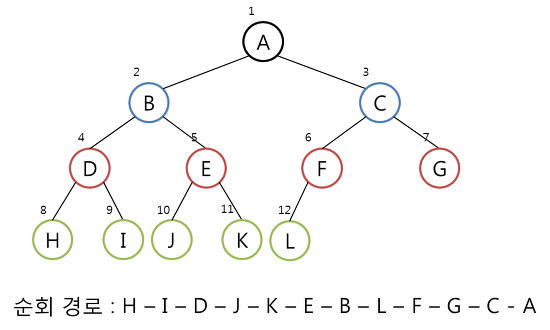
- Postorder 운행(후위 순회)
- LEFT -> RIGHT -> ROOT 순으로 운행한다.
- Preorder 운행 (전위 순회)
Preorder 운행법의 방문 순서
Inorder 운행법의 방문 순서
Postorder 운행법의 방문 순서
3. 수식의 표기법
산숙실을 계산하기 위해 기억공간에 기억시키는 방법으로 이진 트리를 많이 사용한다. 이진 트리로 만들어진 수식을 인오더, 프리오더, 포스트오더로 운행하면 가각 중위, 전위, 후위 표기법이 된다.
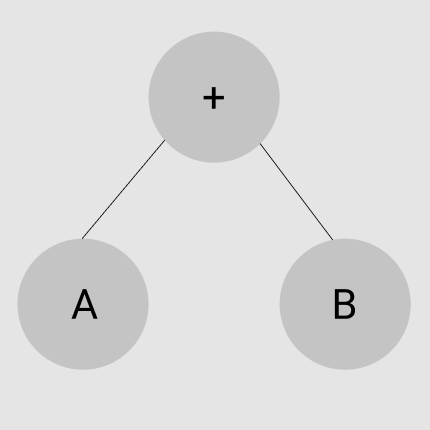
- 전위 표기법 (PreFix) : 연산자 -> LEFT -> RIGHT
- 중위 표기법 (InFix) : LEFT -> 연산자 -> RIGHT
- 후위 표기법 (PostFix) : LEFT -> RIGHT -> 연산자
Infix 표기를 Prefix로 변환하기
X = A / B * (C + D) + E
-
(X = (((A / B) * (C + D))+E)) : 연산 우선순위에 따라 괄호로 묶는다.
-
=(X+(*(/(A B)+(C D))E)) : 연산자를 해당 괄호 앞으로 옮긴다.
-
=X+*/AB+CDE : 필요 없는 괄호를 제거한다
Infix 표기를 Postfix로 변환하기
X = A / B * (C + D) + E
-
(X = (((A / B) * (C + D))+E)) : 연산 우선순위에 따라 괄호로 묶는다.
-
(X(((A B)/(C D)+)*E)+)= : 연산자를 해당 괄호의 뒤로 옮긴다.
-
XAB/CD+*E+= : 필요 없는 괄호를 제거한다.
Postfix 표기를 Infix로 변환하기
A B C - / D E F + * +
-
((A (B C -) /) (D (E F +) *) +) : 먼저 인접한 피연산자 두 개와 오른쪽 연산자를 괄호로 묶는다.
-
((A / (B - C)) + (D * (E + F))) : 연산자를 해당 피연산자의 가운데로 이동시킨다
-
A / (B - C) + D * (E + F) : 필요 없는 괄호를 제거한다.
Prefix 표기를 Infix로 변환하기
- / A - B C * D + E F
-
(+ (/ A (- B C)) (* D (+ E F))) : 먼저 인접한 피연산자 두 개와 왼쪽 연산자를 괄호로 묶는다.
-
((A / (B - C)) + (D * (E + F))) : 연산자를 해당 피연산자의 가운데로 이동시킨다
-
A / (B - C) + D * (E + F) : 필요 없는 괄호를 제거한다.
