Computer Architecture L03

Instruction Types

• Operate instructions: ALU가 계산하는.. (ex. ADD, SUB)
• Data movement instructions: MEM에서 R/W하는.. (ex. LOAD, STORE)
• Control flow instructions: 실행 순서 바꾸는.. (ex. BEQ, BNEQ)
  
  

Assembly Language

• The human-readable representation of 'instructions' or 'machine language'
• Has a direct mapping btwn assembly code and instructions (기계어)
  
  

---

von Newmann Model Properties

• Stored Program
  Instructions stored in a linear memory array together
  Memory is unified between instructions and data
  -> Control signal에 따라서 해당 값이 instr인지 data인지 판단
  
  
• Sequential instruction processing
  PC는 branch 등의 경우를 제외하고는 순서대로 instruction을 실행
  
  

Preview(?): ISA specifies..

• Memory organization (메모리가 어떻게 구성되어 있는지)
  Address space, Addressability (Word- or Byte- addressable)
• The register set (레지스터의 개수)
• The instruction set (instruction의 구성)
  Opcodes, Data types, Addressing modes, Length... 등등

---

Preview(?): Microarchitecture

마이크로아키텍처: 일종의 설계도 느낌!

• Architecture: visible to the software
  Address space, addressability, opcode 등....
• Microarchitecture: not visible to the software
  cache, instruction cycle, pipelining 등...
  
  
  

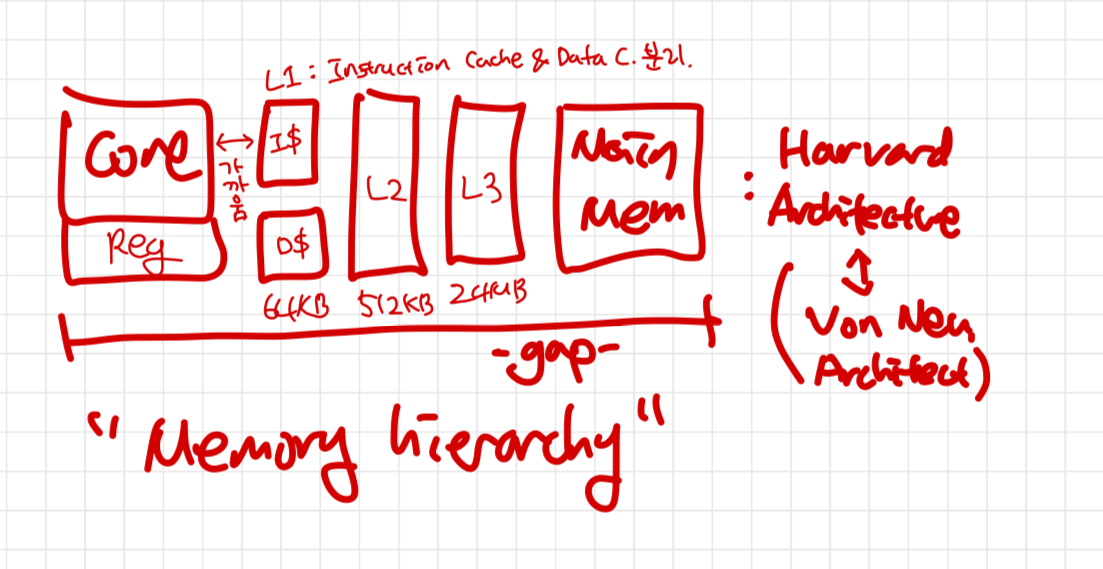
Memory hierarchy

---

Basic Metrics

Latency or delay (저저익선)

특정 일을 얼마나 빨리 하는 지!
단위: 초 (ms($10^{-3}$s), us($10^{-6}$s), ns($10^{-9}$s), ps($10^{-12}$s))

A measured latency is for some particular task!

A CPU doesn't have a latency (CPU는 실행의 '주체'니까)
An application has a latency on a particular CPU

Throughput (고고익선)

같은 시간에 일을 얼마나 많이 하는 지!
단위: 속도(?) (bytes/s, instrs/s, instrs/cycle)

Cost

🤑 ㅋㅋ

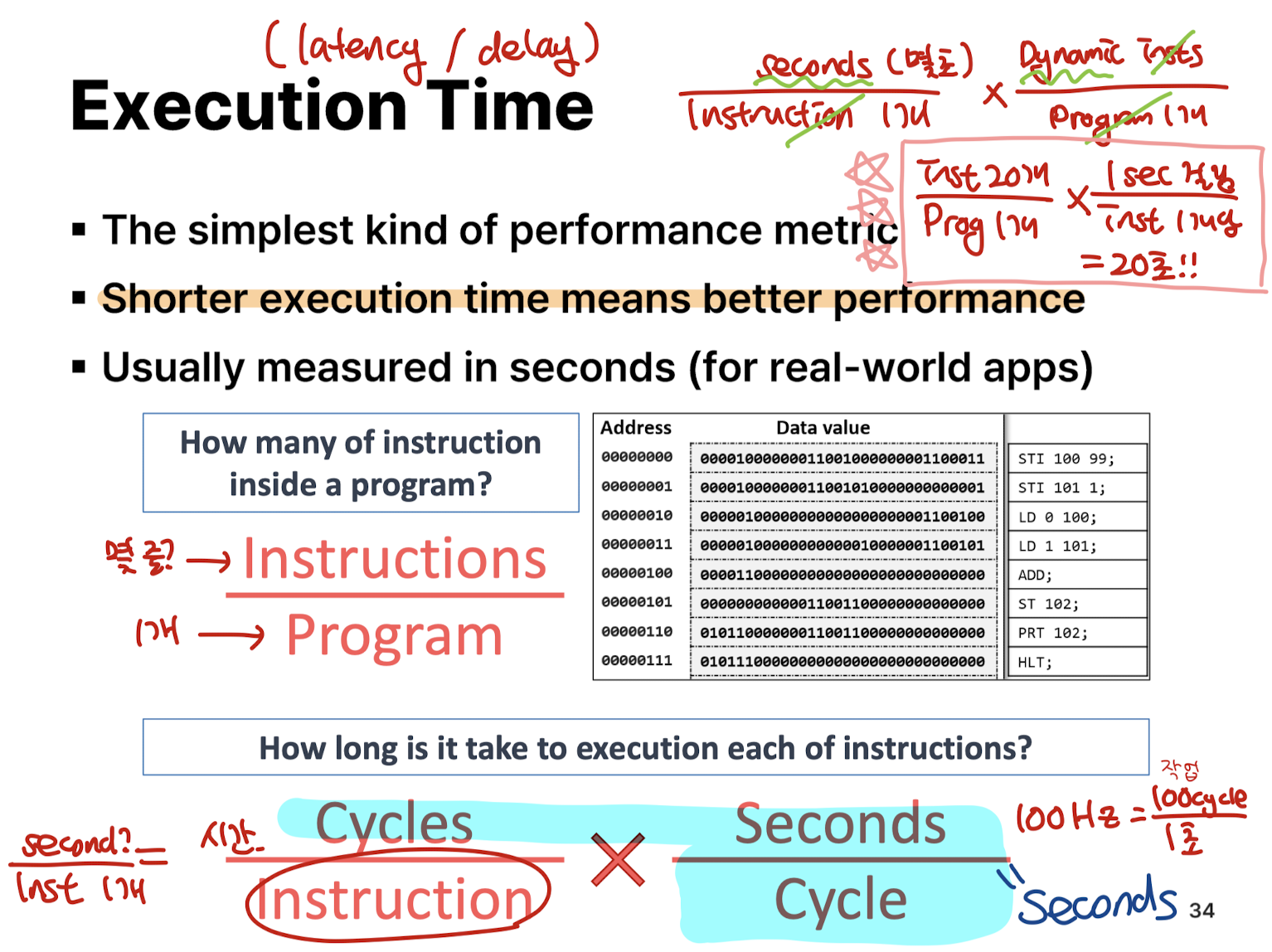
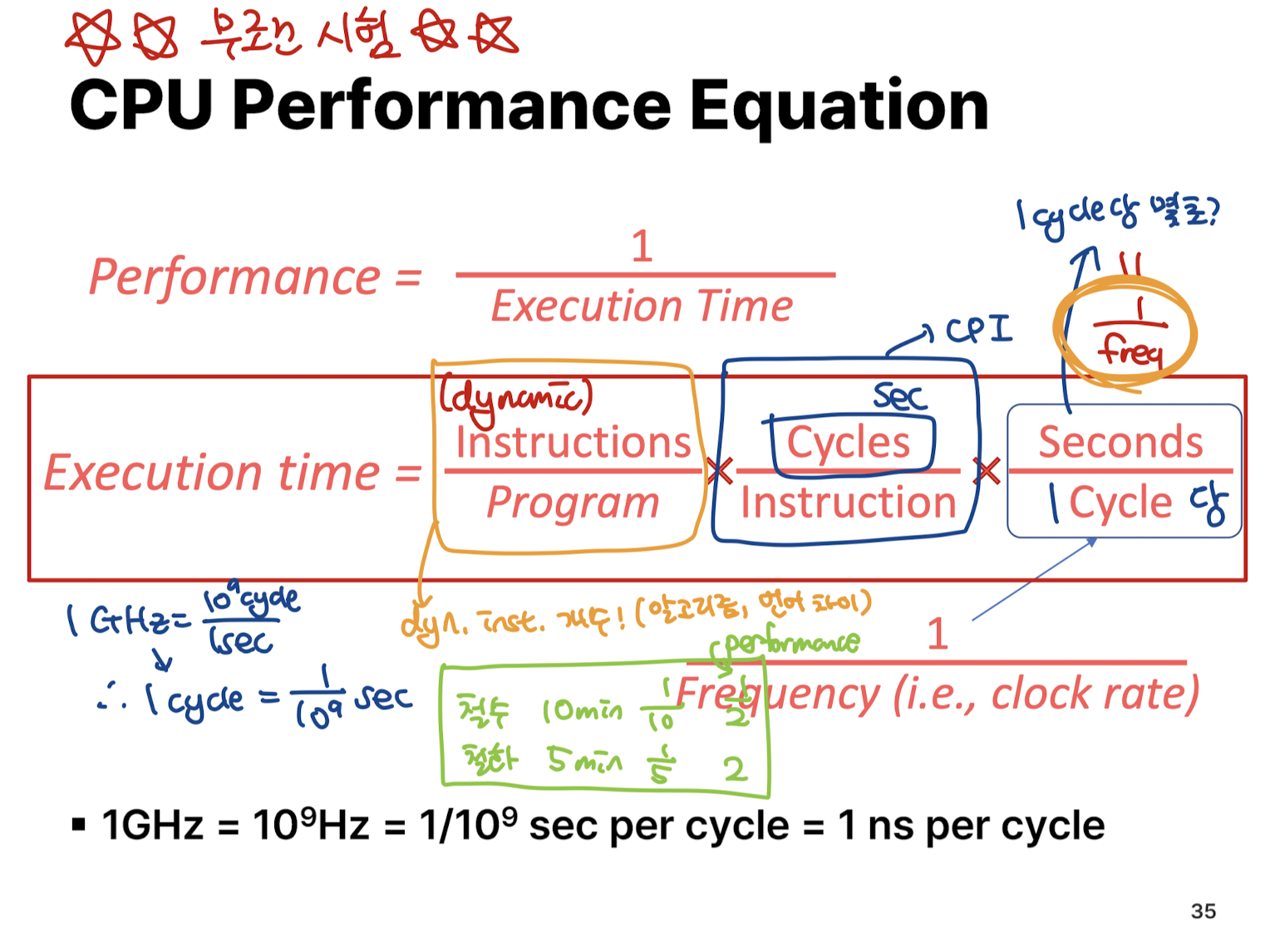
Execution Time (매우 중요!!!)

요건 피피티 필기자료로 대체~! (수식 표현하기 어려워잉..)

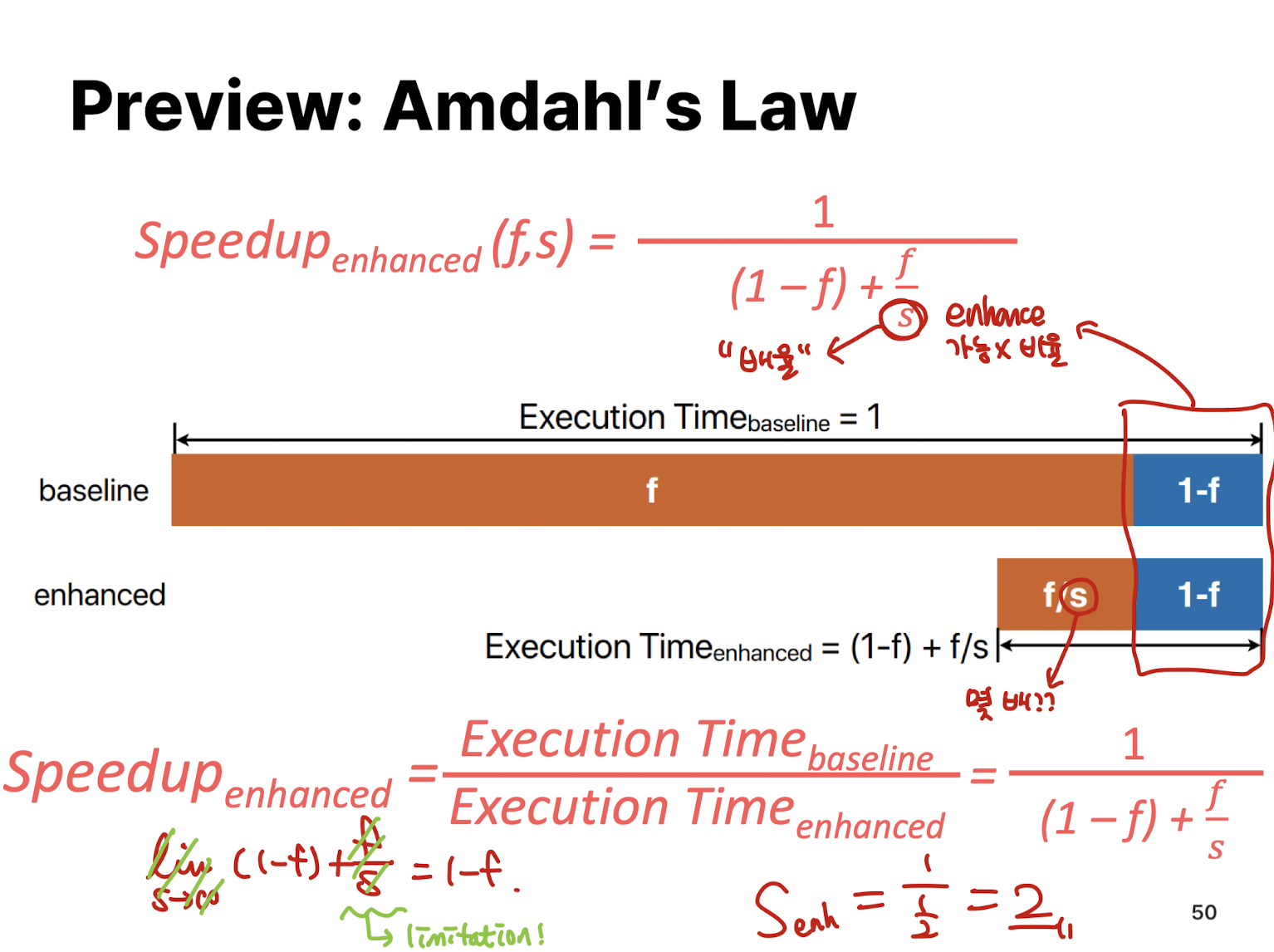
Amdahl's Law

얘도 수식이라서.. 스샷으로 대체

Comparing Performance

• A is X times faster than B if
  - Latency(A) = Latency(B) / X
  • Throughput(A) = Throughput(B) * X
• B is X% faster than B if
  - Latency(A) = Latency(B) / (1+X/100)
  • Throughput(A) = Throughput(B) * (1+X/100)

‼️ 예를 들어서 5배는 500%가 아닌 400%임! 계산할 때 조심하기

Mean (Avg) Performance Numbers

• Arithmetic (산술평균): 우리가 알고있는 그 엔빵 ^^
  치명적인 단점은.. 각 배율값(?)을 더해서 나누면 결과 처참해짐 -> 기하 사용
• Harmonic (조화평균): 대역폭이나 성능 구할 때 사용
  "For units that are inversely proportional to time (kbps, mbps..)"
  뒤집어서 더하고 다시 뒤집기!
• Geometric (기하평균): 배율 구할 때 굿 (speedup ratios)
  n개의 값을 각각 곱하고 n제곱근 값 구하기

---

Summary