[JavaScript] Data Structure - Linked List

Intro.

연결 리스트에 대한 비유는 뭐가 좋을까 생각하다가 방탈출이 생각났다. 얘도 코로나 때문에 가지 못하는 곳 중 하나인데, 까마득한 옛 기억을 더듬어보면 다음과 같다.

나는 무슨무슨 임무를 가진 에이전트. 적들의 함정에 빠져서 이 방 안에 갇혔다. 
적들의 목적은 앞으로 1시간 후 뉴욕을 폭파하는 것이다. 
나는 1시간 안에 이 방을 탈출해서 그들을 막아야 한다!

뭔가 방탈출은 이런 오글오글한 스토리로 시작하는 것 같던데ㅋㅋㅋ 몰입도를 위해서 한 번 따라해봤다. 아무튼 눈에 안대를 쓰고 팔목에 수갑을 찬 채로 조그만 방에 갇히고 나면 방탈출이 시작된다. 방탈출에서 가장 빡치는 점은 상자 A를 찾으면 그 안에 다른 상자 B를 위한 단서가 있고, B 상자 안에는 또다른 상자 C를 위한 단서가 있다는 것이다. 상자 A를 찾지 못하면 상자 B를 열 수가 없고, 그렇다면 상자 C 역시 열 수가 없다. 이렇게 연속적으로 다음 상자에 대한 단서를 가지는 것을 연결 리스트에 비유할 수 있지 않을까..? 완벽한 비유는 아니겠지만.

Linked List란?

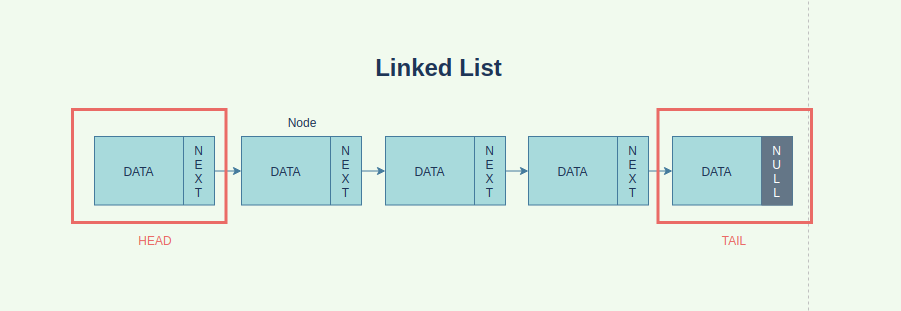
연결 리스트Linked List는 데이터를 저장하는 자료구조 중 하나이다. 연결 리스트는노드Node라고 불리는 데이터 구조들이 일렬로 연결된 구조를 가지고 있으며, 각각의 노드는 '데이터Data'와 '다음 노드의 정보Next'를 갖는다. 방탈출 비유에서 상자는 '노드'를, 다음 상자를 열 수 있는 열쇠는 '다음 노드의 정보'를 가리킨다고 할 수 있다. '데이터'는..? 데이터는 상자의 내용물, 말 그대로 노드에 저장된 데이터이다. 상자에 실뭉치가 담겨있다면 데이터는 실뭉치, 마네킹 손이 담겨있다면(도대체 공포 방탈출이 아닌데도 이런 걸 담아두는 건 뭐지ㅠㅠㅠ) 마네킹 손이 해당 노드의 데이터라고 볼 수 있다.
연결 리스트의 맨 처음의 노드를 head라고 하며, 마지막 노드를 tail이라 부른다.(tail을 찾으면 방을 탈출할 수 있다)

Linked List의 시간복잡도

그럼 왜 굳이 이런 방식의 자료구조를 사용할까? 이 자료구조는 수정, 즉 삽입과 삭제가 빈번하게 일어나는 상황에 유용하다.

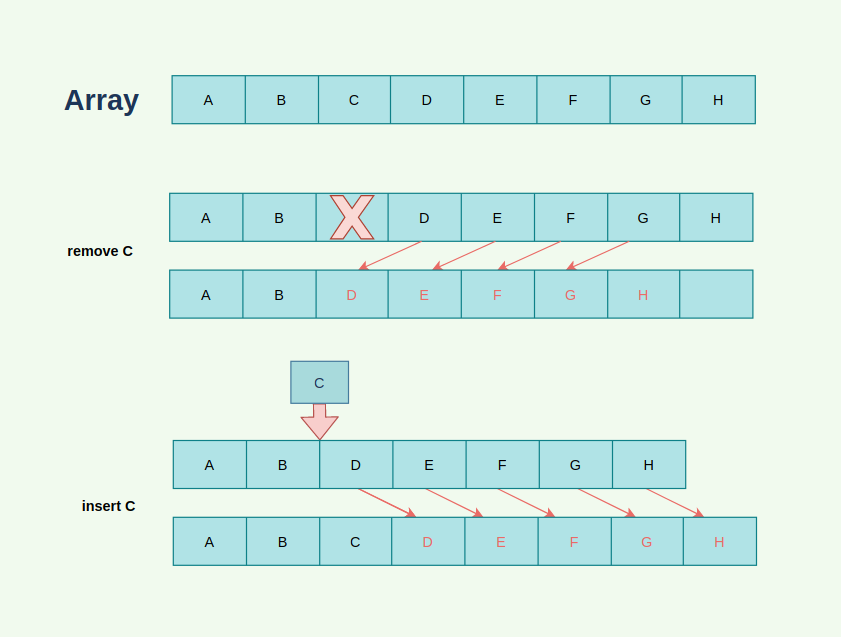
연결 리스트와 흔히 비교되는 대상은 배열인데, 배열을 칸막이 책장으로 비유해보자. 배열은 각 데이터를 순서대로 책장의 칸막이에 하나씩 넣는 자료구조다. 즉, 상자 A의 데이터는 1번 칸에, B는 2번 칸에, C는 3번 칸에.. 이런 식으로 10개의 데이터가 순서대로 나열되어 있다고 하자. 만약 상자 C가 불필요하다고 생각해서 제거해야 하는 경우, 뒤에 있는 D, E, F, G 등등의 친구들을 C가 있던 자리부터 앞으로 한 칸씩 땡겨 와야 한다.(정확히 말하면 C를 제외한 A부터 J까지의 친구들을 모두 새로운 배열로 옮겨주는 과정을 거친다.) 만약 이 상태에서 C를 다시 원래의 자리로 삽입한다면? (장난해?) 이 역시 번거로운 작업이다. 데이터들을 하나하나 다시 자리배치를 해주어야 하는 것이다.

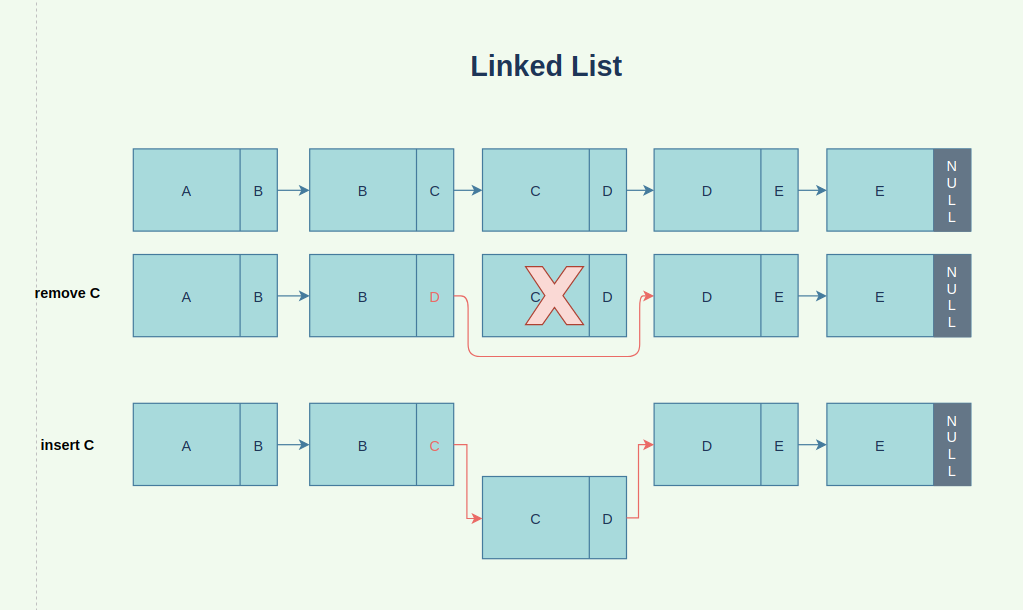
반면 연결리스트는 간단하다. C를 제거한다고? 그럼 상자 B에서 C의 열쇠를 제거하고 그 안에 D의 열쇠를 넣어두면 된다. C를 다시 원래 자리에 추가한다고? 그럼 상자 B에 C 열쇠를 두고, 상자 C 안에는 D 열쇠를 넣어두면 된다. 간단하다! (draw.io로 그리는 건 간단하지 않았다.. 그림이 개떡같아도 찰떡같이 이해해주시길..)

즉 연결 리스트는 삽입과 삭제에 O(1)의 시간복잡도를 가진다. 그러나 만일 탐색의 경우(그러니까 상자 E를 열어야 한다면) 앞선 노드들을 모두 거쳐야만 해당 노드의 데이터를 알 수 있기 때문에 최악의 경우 O(n)의 시간복잡도를 가진다.

삽입과 삭제

• 배열 : O(n)
• 연결리스트 : O(1) (다만 탐색 과정 이후에 삽입과 삭제를 하기 때문에, 삽입과 삭제 과정 자체는 O(1)이지만, 전체 과정으로 본다면 O(n)이다.)

탐색

• 배열 : O(1) <- 데이터의 인덱스만 알고 있으면 바로 찾을 수 있다.
• 연결리스트 : O(n)

Linked List의 활용

음악을 들을 때 재생 버튼 양 옆으로 뒤로 가기, 앞으로 가기 아이콘이 있는 것을 볼 수 있을 것이다. 뒤로 가기 아이콘을 누르면 이전 음악으로, 앞으로 가기 아이콘을 누르면 다음 음악으로 넘어가는데 이는 연결리스트를 활용한 예제 중 하나이다. (정확히 말하면 double linked list를 활용한 것이다)

또한 브라우저의 뒤로가기, 앞으로가기 버튼도 마찬가지이다. 방문한 페이지 목록은 연결 리스트로 연결되어 서로의 앞 뒤 페이지로 넘어갈 수 있다. (이것도 역시 double linked list)

블록체인은 이전 블록이 다음 블록으로 체인처럼 연결되는 구조로 되어 있어, 이 역시 연결리스트 방식으로 연결되어 있다고 볼 수 있다.

Double Linked List

연결 리스트에는 단일 연결 리스트(Singly-Linked List), 이중 연결 리스트(Doubly-Linked List) 등이 있다. 말 그대로 단일 연결 리스트는 head에서 tail까지 한 방향으로 연결된 연결 리스트를 말하며 여태까지 설명한 연결 리스트이다. 반면 이중 연결 리스트는 각 노드가 previous와 next를 가졌기 때문에 양 방향으로 탐색이 가능한 연결 리스트를 말한다.

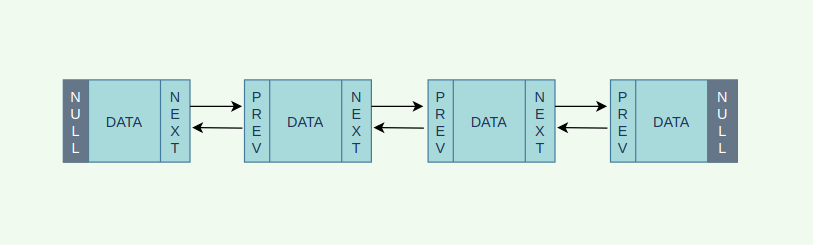
이중 연결 리스트는 각각의 노드가 다음 노드의 정보뿐 아니라 앞의 노드 정보도 가지고 있어 양방향 탐색이 가능하다. 대신 단일 연결 리스트보다 메모리를 더 잡아먹는다는 단점이 있다.

Linked List 구현을 위한 의사코드

// node를 class로 구현한다
class Node { 
  constructor(value) {
    this.value = value;
    this.next = null;
  }
}

class LinkedList {
  constructor() {
    this.head = null;
    this.tail = null;
    this._size = 0;
  }
  // 주어진 값을 연결 리스트의 끝에 추가하는 메소드
  addToTail(value) {
    // node 클래스를 기반으로 value를 속성으로 갖는 새 인스턴스를 생성한다
    
    // 만약 첫 노드라면
    // head는 이 노드이고
    // tail도 이 노드이다.
    
    // 아니면
    // 현 tail의 next에 새 노드를 추가하고
    // 새 노드가 새로운 tail이 된다.
    
    // size가 1 증가한다.
  }
  
  // 주어진 값을 찾아서 연결을 해제(삭제)하는 메소드
  remove(value) {
    // 만약
  	// head의 value가 value와 같다면
    // 기존 head의 다음 노드를 새 head로 재할당한다.
    
    // 아니면
    // 이전 노드를 담을 변수를 선언한다.
    // 현재 노드를 담을 변수를 선언한다.
    // while 반복문으로 현재 노드의 value가 value와 같을 때까지
    	// 이전 노드는 현재 노드로 이동하고
    	// 현재 노드는 다음 노드로 이동한다.
    // 반복문이 끝나면 이전 노드의 next에는 현재 노트의 next를 재할당한다.
    
    // size가 1 감소한다.
  }

  // 주어진 인덱스의 노드를 찾아서 반환하고, 없다면 undefined를 반환하는 메소드 
  getNodeAt(index) {
    // 현재 노드를 담을 변수를 선언한다.
    // 카운트를 담을 변수를 선언한다.
    // while 반복문으로 카운트가 인덱스와 같을 때까지
    	// 만약
	// 현재 노드가 null이라면
    	// undefined를 리턴한다.
    
    	// 아니면
    	// 현재 노드는 다음 노드로 이동한다
    	// 카운트가 1 증가한다.
    // 반복문이 끝나면 현재 노드를 리턴한다.
  }

  // 연결리스트에 주어진 값을 가지는 노드의 존재 여부를 반환하는 메소드
  contains(value) {
    // 현재 노드를 담을 변수를 선언한다
    // while 반복문으로 현재 노드의 value가 value와 같을 때까지
    	// 현재 노드는 다음 노드로 이동한다
    	
    	// 만약
    	// 현재 노드가 null 이라면
    	// false를 리턴한다.
    
    // 반복문이 끝나면 true를 리턴한다.
  }

  // 주어진 값의 인덱스를, 없을 경우 -1을 반환하는 메소드
  indexOf(value) {
    // 현재 노드를 담을 변수를 선언한다.
    // 카운트를 담을 변수를 선언한다.
    // while 반복문으로 현재 노드의 value가 value와 같을 때까지
    	// 현재 노드는 다음 노드로 이동한다
    	// 카운트가 1 증가한다.
    
    	// 만약
	// 현재 노드가 null이라면
    	// -1를 리턴한다.
    
    // 반복문이 끝나면 카운트를 리턴한다.
  }

  size() {
    // size를 리턴한다.
  }
}