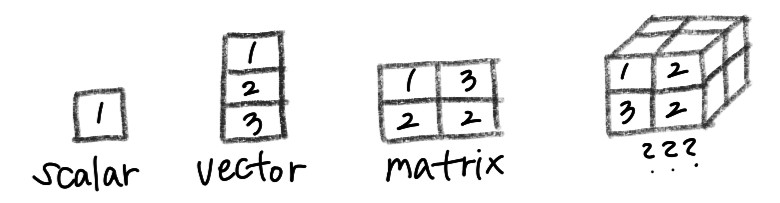Tensor란

neural network에 들어가기 앞서, 기본적인 개념으로 Tensor를 알고 넘어가야한다. 이는 수학적인 개념으로 데이터의 배열이라고 보면 된다. 우리가 흔히 아는 차원의 개념의 데이터는

• 0차원 : scalar(스칼라)
• 1차원 : vector(벡터)
• 2차원 : matrix(행렬)

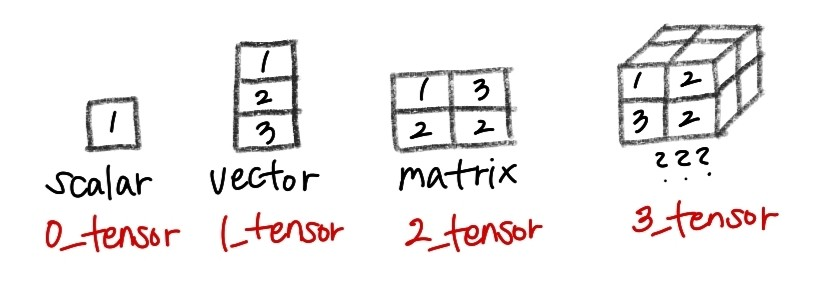
이다. 맞다.... 3차원부터는 뭐라고 설명해야할지 잘 감이 잡히질않는데 사실 이 모든게 바로 Tensor인 것이다. scalar부터 차례로 Rank(차원의 수)가 0,1,2,3인 Tensor인 것이다.

Tensor 사용 이유

사진, 음성, 텍스트 파일 모두 결론적으로 수학적인 계산을 할 수 있게 수치화하여 모델에 입력되게 된다.
이때 입력되는 형식을 Tensor라고 보면 편하다.

ex)

• 모델에 값 하나하나를 scalar로 입력하게 되면, 100개의 사진(해상도 100*100)을 입력한다고 쳤을때, 1,000,000개를 동시에 입력해야함
• Tensor형태로 입력하게 되면, 100개의 100*100 행렬을 입력하면 됨

같은 양을 의미하는 데이터를 더 효율적으로 입력이 가능하고, GPU 메모리에 자료형을 올려서 병렬연산이 가능하기 때문에 더더욱 해당 데이터를 사용해야하는 것이다. 이제 model에서의 데이터형식 tensor에 대해 어느정도 이해를 했으니 NN에 대해 알아보자.

Neural Network(NN)

NN(ANN)은 인간의 신경망 구조에 영감을 받아 만들어진 computing system이다. Deep Neural Network에 대해 정의하기 전에 Perceptron에 대한 개념이 필요하다.

퍼셉트론(perceptron)?

퍼셉트론은 쉽게 인공신경망 모형의 한 종류이다. Perception(인지하는 능력)+ Neuron(뉴런, 신경세포) 를 조합한 단어로 인지한 것을 뉴런처럼 동작하는 인공신경망이라는 뜻을 가진다.

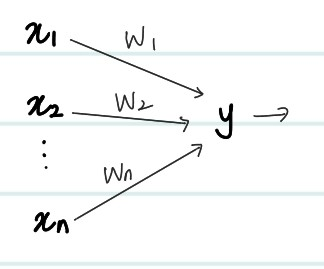
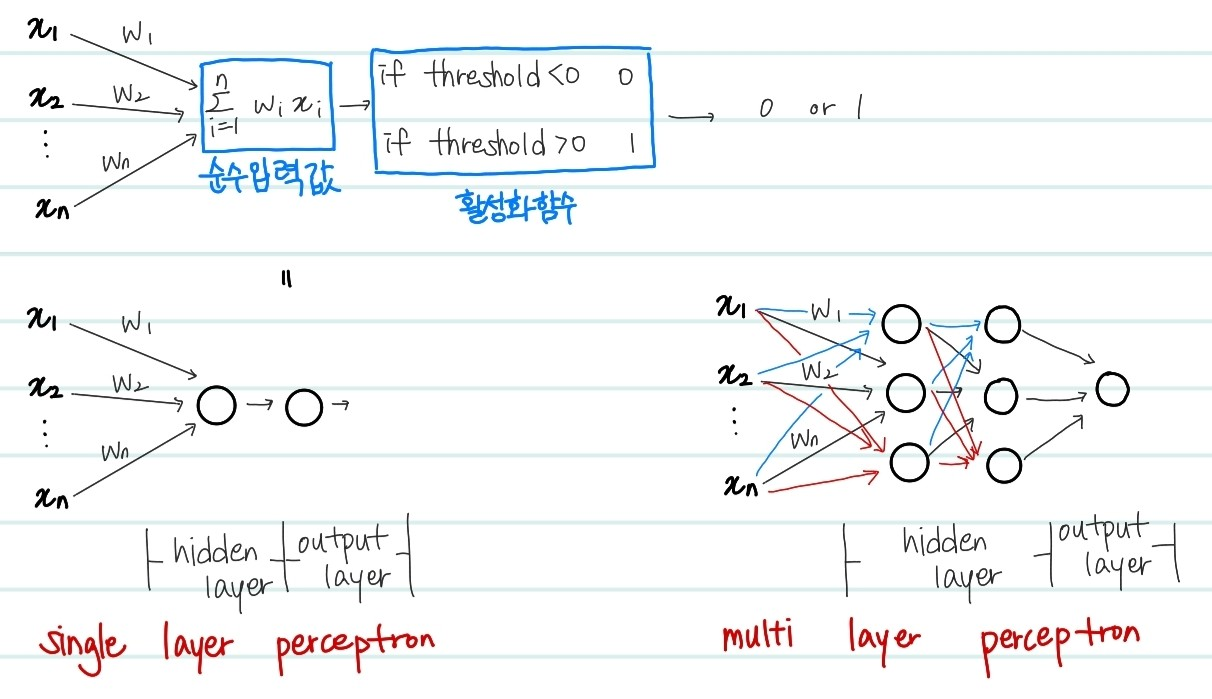
위는 퍼셉트론의 구조에 대한 그림이다. 퍼셉트론은 다양한 입력을 받아서 어떠한 신호 결과값을 출력한다.

각각의 입력에는 출력에 대해 해당 입력이 행사한 영향력을 나타내는 지표로 가중치인 weight가 부여되어있다. 즉 여러개의 고려사항을 input으로 설정한뒤, 각 고려사항에 대한 weight parameter를 모델이 학습해나가는 과정이라는 것을 알 수 있다. 그 학습하는 기준은 바로, 모델이 예측하게 된 predicted_y값과 실제 값인 true_y값의 차이 등의 loss에서 구하는 것이다.

Single-Layer Perceptron

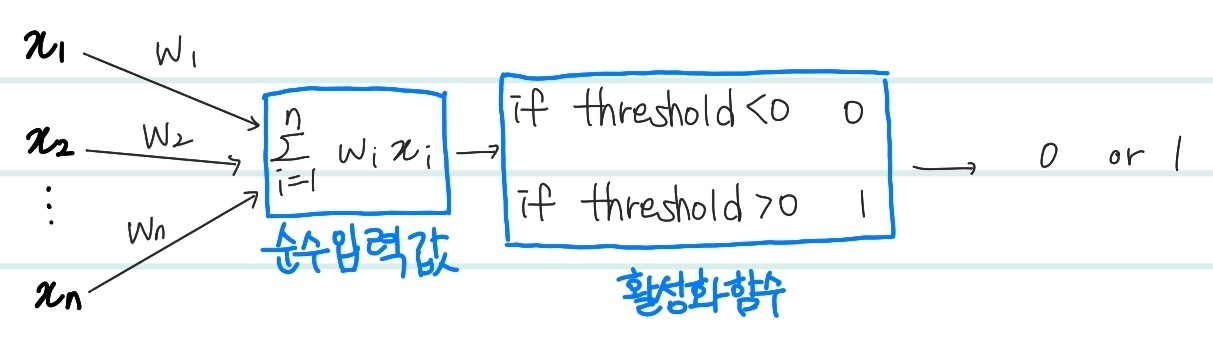
위의 perceptron에 대한 구조에서 조금 더 자세하게 그린 구조도이다. 특성값 $x_0$~$x_n$과 가중치 $w_0$~$w_n$의 곱한후 다 더하여 만든 값을 순입력 함수 라고 한다. 그리고 이 값을 threshold 기준으로 작으면 0 크면 1로 결과를 나오게하는 함수를 활성화함수(activation function)이라고 한다. 활성화함수는 현재 필자가 임의로 작성한 함수로, 다양한 종류의 활성화 함수가 존재한다. (Relu,tanh,Gelu 등) 위는 은닉층이 1개이며 그 은닉층에서의 노드 수도 한개인 경우이지만, 해당 노드가 여러개가 될 수 있고 은닉층 자체도 여러개가 될 수 있다. 이를 Multi-layer Perceptron이라고 한다.

Multi-Layer Perceptron

multi layer perceptron은 비선형 분류를 가능하게 해준다. 이는 간단하게 논리 게이트인 AND, OR, NAND, XOR 게이트를 예시로 알 수 있다. single layer perceptron 은 선형으로 분류되지 않는 데이터에 대해서는 분류가 불가능해 XOR 게이트를 구현할 수 없다. 아래의 그림을 살펴보자.

input $x_1$ , $x_2$ 을 그래프로 나타내면 위와 같다.

파란색: input값이 서로 다른 값 → 1
빨간색: input값이 같은 값 → 0

위의 두 색의 점은 직선으로 구분할 수 없다.따라서 layer를 추가함으로써, 여러 activation function을 거치며 비선형성을 만들어내 위의 XOR게이트 와 같은 비선형적인 문제를 해결하는 것이다. 이때, activation function의 역할이 굉장히 중요하다 아래의 경우를 비교해보자

Activation function의 중요성

Linear score function : $f=Wx$
2-Layer Neural Network : $f=W_2\,max(0,W_1x)$

위의 예시에서는 max(0,z)가 activation function이다. 만약에 activation function이 존재하지않다면 2-Layer Neural Network는 $f=W_2W_1x$가 될 것이다. 이는, $W_1,W_2$가 하나의 가중치 $W$로 봐도 되는 것이다. 즉 비선형성을 잃게 된다. 따라서 비선형성을 유지하기 위해서 activatoin function을 사용해야하는 것이다.

Activation function의 종류

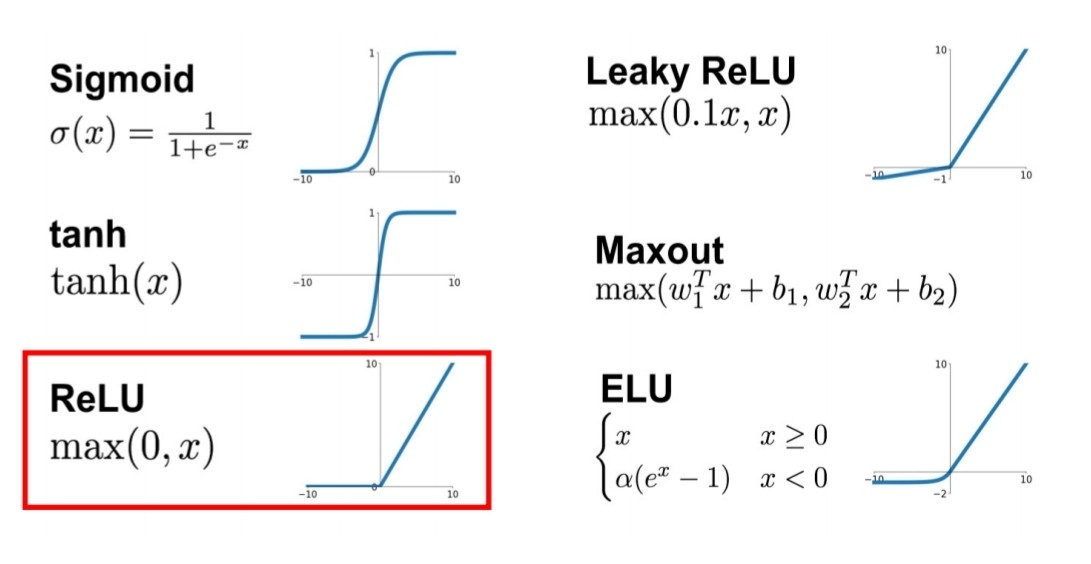위의 사진에서 보이는 다양한 종류의 activation function이 존재한다. 그 중에서도 0이하의 값은 0으로 output이 설정되고, 0이상의 값은 그 값을 그대로 return 하는 ReLU 활성화 함수를 많이 사용한다. 또한, sigmoid 함수는 출력값을 0에서 1사이의 확률값으로 출력하기 위해서 사용한다. 다양한 상황에 맞춰서 적합한 activation function을 사용한다.