Backpropagtion?

back propagtion은 쉽게 Neural Network의 가중치를 학습시킬 때 사용되는 알고리즘이다. 모델이 마지막 output layer에서 예측한 predicted value와 실제 값인 target value의 차이가 얼마인지 구한다.그 후, 그 오차 값을 뒤로 전파해 신경망의 각 노드에 있는 가중치를 갱신하는 알고리즘이다.

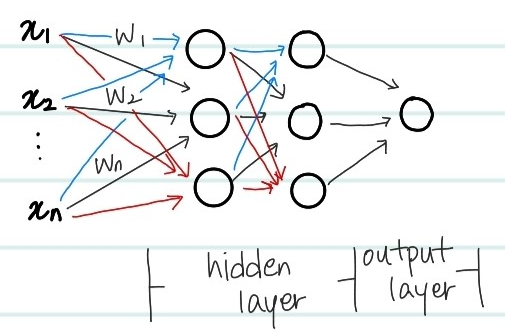
위 사진은 이전 포스트에서 등장했던 multi layer perceptron이다. back propagtion은 위의 값 중, w값을 업데이트하는 알고리즘인 것이다. 여기서 Neural Network의 궁극적인 목표는 Model의 output이 실제 true value와 유사하게 되게끔 노드의 가중치를 update하는 것임을 잊어서는 안된다. 따라서, 초기의 할당된 가중치에 따른 모델의 예측값과 실제값의 차이를 계산하고 이를 활용해서 모델 내 가중치를 수정하는 것이라고 이해하면 편하다.

---

Chain Rule

어려워보이지만 굉장히 간단한 개념 Chain Rule 바로 미분의 연쇄법칙이다. 수식은 아래와 같다.

$f,g$모두 미분이 가능하고,
$F=f(g(x))$ 로 정의된 합성함수면 $F$는 미분이 가능하다.
이때, $F'(x)=f'(g(x))\cdot g'(x)$ 이다.

이 합성함수 미분을 사용하는 이유는, 기울기 자체는 변화량이라는 뜻도 가진다. 즉, 위의 경우

• $x$의 변화에 의해 $g$함수가 얼마나 변하는지,
• $g$의 변화에 의해 $f$함수가 얼마나 변하는지,
• $f$의 변화에 의해 $F$함수가 얼마나 변하는지를 알 수 있다.

즉, 각각의 함수에 의해서 최종적으로 $F$가 얼마나 변하는지 그 기여도를 알 수 있다. 이를 가중치에 대입해보면, 각각의 feature에 대한 weight가 모델의 output에 얼마나 기여하는지를 알 수 있고, 그 output이 실제 값과 차이를 보일 때, weight를 update해 더 정밀한 output을 모델이 낼 수 있도록 하는 것이다.

Chain Rule with many variables

변수가 여러개인 경우도 생각해볼 수 있다. 예를들어,

$z=f(x,y)$이고, ( $x=h(s,t)$, $y=g(s,t)$ )

에 대해서, $f,h,g$함수 모두 미분이 가능하다면, $z$를 $s$, $t$ 로 미분 하였을 때를 아래와 같이 표현할 수 있다.

$\frac {\partial z} {\partial s}=\frac {\partial z}{\partial x}\frac {\partial x}{\partial s}+\frac {\partial z}{\partial y}\frac {\partial y}{\partial s}$
$\frac {\partial z} {\partial t}=\frac {\partial z}{\partial x}\frac {\partial x}{\partial t}+\frac {\partial z}{\partial y}\frac {\partial y}{\partial t}$

s,t의 변화에 의해 z가 변화했을 때 수식으로 표현이 가능하고, 편미분을 적용하기 때문에, s와 z의 관계에선 t에 대해선 고려하지 않아도 된다.

여기까지의 Chain Rule에 대한 설명에 대해 이해를 했다면 Back propagation에 대해 이해할 수 있다.

---

Feed Fowarding

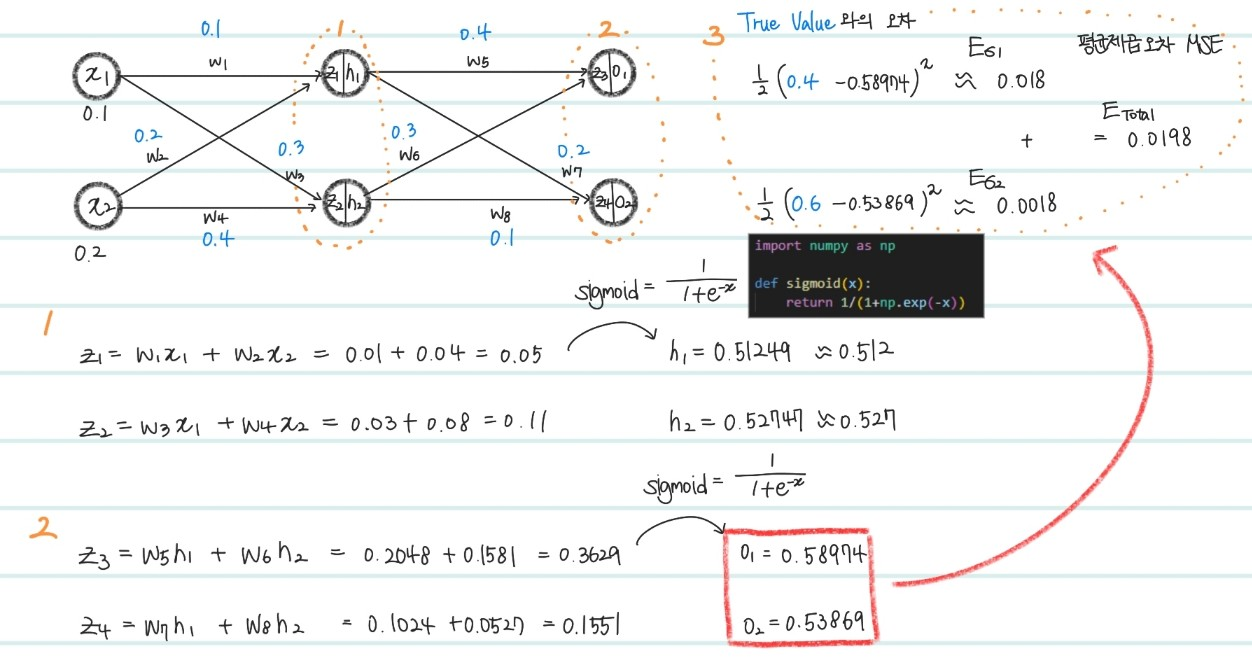
위는 Back Propagation이 있기전의 Feed Forwarding의 과정이다. 먼저, 검정,파랑색으로 적혀있는 수들은 최초에 임의의값으로 초기화됨을 의미한다.

1. 각각 weight와 input을 곱하여 hidden layer의 노드에 해당하는 값들을 더한 뒤, sigmoid함수(activation)를 취한다.
2. output layer상에서도 마찬가지로 hidden layer를 지나 발생한 $h_1$, $h_2$ 값을 output layer의 input으로 입력한뒤, sigmoid 함수를 거쳐 최종 output value를 산출한다.
3. True value와 최종 output value간의 MSE(평균 제곱 오차)를 사용한다.
   📌 MSE : $\frac 1 n\sum_{i=1}^n(y_i-t_i)^2$

모든 case에 대해 평균 제곱 오차를 구하니, 0.0198이 나왔다. 이렇게 input 단 부터 output 단 까지의 계산을 마친 뒤, 오차를 구하는 과정을 feed forward 라고한다.

---

Back Propagation

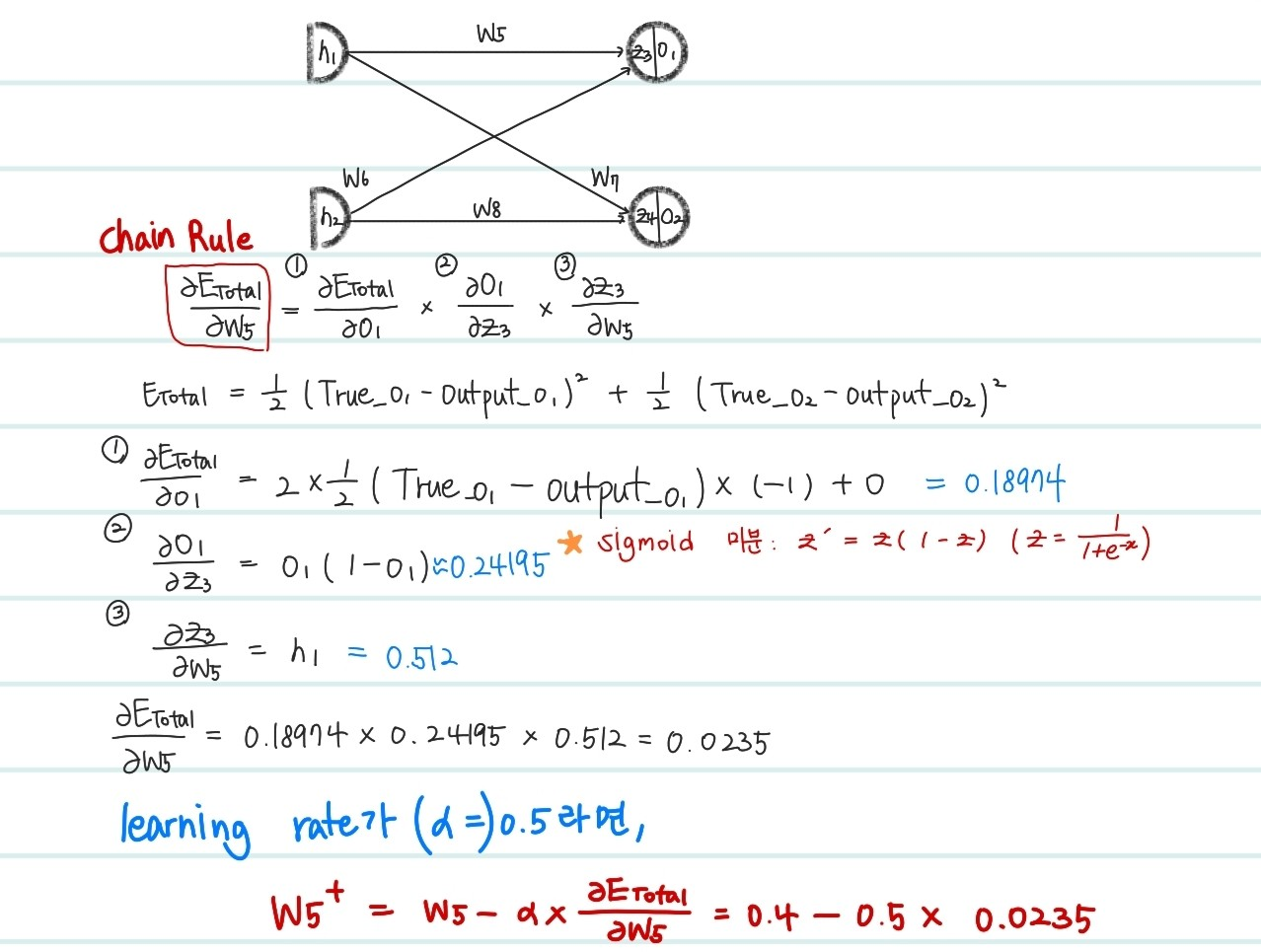
Feed Forwarding을 통해서 출력값을 얻었다면, Back Propagation은 가중치를 업데이트하기 위한 과정이다. 참고로 가중치는 loss에 대한 가중치의 미분값에 따라 결정된다. 미분값이 양의 값이 나온다면 가중치를 감소시키고, 음의 값이 나오면 증가 시키기 위해서 수식은 $w=w-\alpha \frac {\partial loss} {\partial w}$ 가 된다. 즉 위처럼 모든 weight에 대해서 Chain Rule을 이용해 미분값을 구한 뒤, learning rate에 맞게끔 가중치를 수정해주는 과정이 Back Propagation이다. 너무 많은 가중치를 수정해야해서, 편의상 $w_5$ 하나만 예시로 작성했다.

위의 과정으로, 각 neuron의 weight값이 loss값에 영향을 준 정도를 계산가능하다. 또한, gradient descent 알고리즘을 활용해서 predict값과 true값의 차이인 loss를 최소화하는 방향으로 neural network의 weight를 수정한다. gradient descent 및 optimization 과정에 대해선 다음 post에서 설명하도록 하겠다.

---

Reference

https://evan-moon.github.io/2018/07/19/deep-learning-backpropagation/