DQN<14> Priority experience replay

김동한·2024년 6월 13일

DRL

목록 보기

14/14

Priority Experience Replay(PER)란

TD(Temporal Difference) error가 큰 것에 우선수위를 부여해, memory에서 batch sample을 추출할때, 더 자주 학습이 이루어질 수 있도록 하는 방법이다.

기본적인 DQN:
memory에서 batch size만큼의 sample을 뽑을 때, 모든 sample에 대해 균등한 확률로 추출한다. 그 후, 추출한 sample에 대한 loss를 줄이는 방향으로 network를 수정한다.

이때, 이미 network가 추출한 sample에 대해서 잘 학습된 상황이라면 다시 굳이 이 sample에 맞게 학습 시킬 필요성은 없다.

PER을 적용한 DQN:
TD error를 통해 각 sample에 대한 우선순위를 둬, error가 큰 case에 맞게 network을 수정할 확률을 높여주는 것이다.

이를 위해서 두가지 방법이 제시되었다

더 의미있는 경험을 저장하자.
2. 경험은 일단 다 저장하고, 의미있는 경험을 추출하자.

replay memory에는 위의 두 가지 방법이 가능하다. prioritized experience replay(PER)는 저장된 경험 중 더 의미있는 경험을 추출하는 것에 초점을 두었다.

Greedy prioritization & Stochastic sampling

Greedy prioritization

TD erorr을 기준으로 가장 높은 순으로 추출해 모델을 학습하는 방법
중요도를 판단해 TD error가 높은 순으로 추출이 가능하게 한다면 성능 향상이 있을 것 같지만, 문제가 발생할 수 있다.

전체 memory에 저장된 sample중 TD error가 높은 sample만 계속 추출되게 된다. 처음에 TD error가 낮게 나온 sample에 대해서는 아예 선택될 기회가 주어지지 않게된다.

결국 소수의 경험에 대해서만 학습한 model이 되어 overfitting돼 일반적인 case에 대한 문제 해결을 못하게된다.

Stochastic sampling

TD erorr을 기준으로 가장 높은 순으로 뽑힐 확률을 크게 하여 추출한 뒤, 모델을 학습하는 방법
중요도를 판단해 TD error가 높은 순으로 추출될 확률을 높게 한다면, 앞서서 TD error가 낮았던 sample이 아예 추출되지 않는 상황을 해결할 수 있게 된다.

한 sample이 뽑히게 될 확률

$P(i)=\frac{p_i^a}{\sum_{k}p_k^a}$

$p_i$ 는 i번째 sample에 대한 priority값이다. $a$ 는 priority가 얼마나 적용되는지 나타낼때 사용하는 hyper parameter이다. $a$ =0 일 때 모든 priority 값에 관련없이 uniform하게 추출하는 uniform sampling과 동일해진다.

$p_i$ 에 대한 정의

propotional prioritization

$p_i=|\delta|+\epsilon$

$\delta$ 는 TD error, $\epsilon$ 은 매우 작은 양수로, $\epsilon$ 은 $p_i$ 가 0 이 되어 확률 계산시 분모가 0이 되는 것을 방지해준다.

rank based prioritization

$p_i=\frac{1}{rank(i)}$

memroy 내에 있는 sample 의 TD error 크기( |δ| )의 순서에 따라 priority를 부여하는 방법이다.

sampling방법에 의한 bias 해결 (importance sampling)

Bias 문제

우선순위가 높을수록 높은 확률로 sampling하기 때문에, 아무래도 우선순위가 높은 sample에 맞게 model이 편향되는 문제가 발생할 수 있다. 이를 해결하기 위해서 학습이 진행될수록 더 uniform하게 sample을 추출할 수 있도록 importance sampling을 진행한다.

importance sampling

대부분 Gaussian 혹은, uniform distribution을 통해 sample을 생성한다. sample을 생성하고 싶은 확률밀도함수에 대해서는 알고 있지만, sample 자체에 대한 생성이 어려울 때, Gaussian, uniform distribution과 확률밀도함수에 대한 관계식을 통해 변환하면 된다.

Uniform distribution

X\text{\textasciitilde}U[0,1] \text{}

확률밀도함수와 랜덤변수 Y에 대한 관계식

Y=g(X)

균등 분포로부터 추출한 sample $x^{(i)}$ 에 대한 변환식

y^{(i)}=g(x^{(i)})

하지만, 복잡한 확률밀도함수에 대해서는 이와 같이 적용하기 힘들다.

따라서 sample 추출 후, expectation을 계산하는 경우, 확률밀도함수보다 sample을 생성하기 쉬운 다른 확률분포함수를 이용해서 추정할 수 있는것이 바로 importance sampling이다.

PER의 경우, priority의 값을 이용해 만든 $P(i)$ 에 대한 expectation을 importance sampling을 통해 uniform 분포를 사용해서 계산하는 방법이다 수식은 아래와 같다.

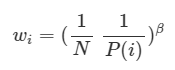
model 학습시 importance sampling weight $w_i$ 를 곱한다. epoch이 진행될수록 $\beta$ 를 1에 가깝게 키워준다. 따라서, uniform distribution에서 sample을 추출하는 것과 동일하게 만들어 주는 것이다. 이해를 돕기 위해 그림을 그려보았다.

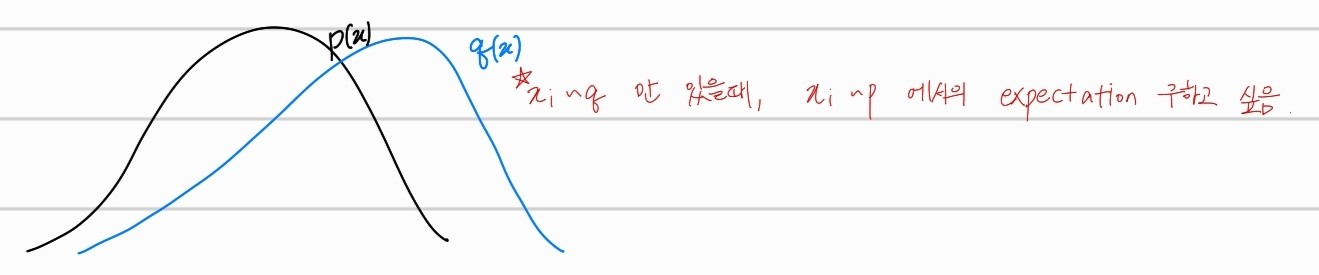
q(x)분포를 p(x)에 맞추어 보는 것이다. q(x)에 대한 sampling값만 존재할때, p(x) 분포에 대한 sampling을 하기 위해 importance sampling을 하는 것이다.

수식의 노란색으로 칠한 부분 xq(x)는 q분포에서의 sample값을 의미한다. 즉 importance sampling weight을 곱하면 q에 대한 sampling값만 존재한 상태에서 p 분포에 대한 sampling값을 얻을 수 있는 것이다.

q(x)는 priority 를 통해서 구했던 $P(i)$ 분포이고, p(x)는 기존의 sampling 분포인 uniform distribution이다.

정리

모델 학습 초기에는 priority를 생각해 우선수위가 높은 값들을 우선적으로 학습하다가, priority가 높은 값들에 대해서 overfitting될 수 있기 때문에, bias를 해결하기 위해 importance sampling weight를 곱하여 학습의 마무리 단계에서는 uniform분포에서의 추출이 가능하게 하는 것이 PER이다.

Forgetful Priority Experience Replay

< $s_t,a_t,r_t,e_t$ >

$\delta$ ( TD error )

( $\delta\times e_t$ ) $^2$ → 시간이 지난 TD error는 가중치 감소

김동한

(●'◡'●)

이전 포스트