Dueling DQN

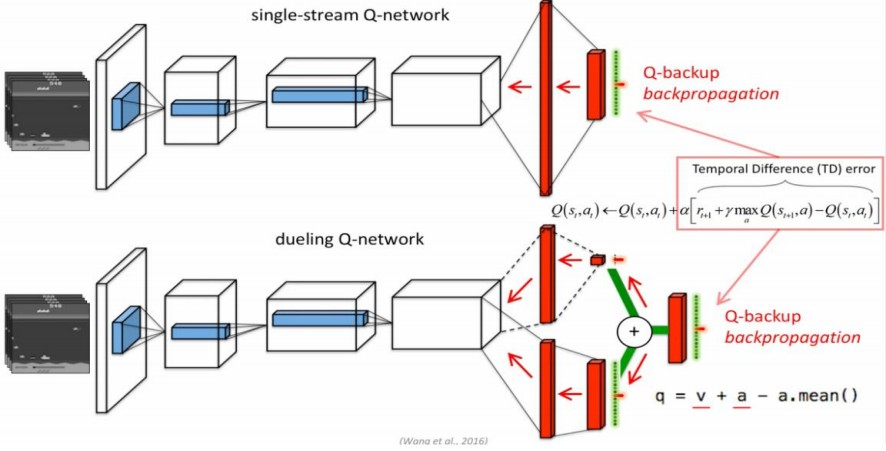
기존 DQN은 CNN을 이용해 Q-network를 구성한다. 기존의 신경망 구조 보다 더 좋은 policy evaluation 즉, 강화학습에 더 특화된 신경망 구조로 성능을 향상시키는 것이다. 어떤 방식으로 성능 향상을 이루어내는지 확인해보자.

---

기존의 DQN은 action만 반영해 network를 update한다. Dueling DQN은 state value도 반영해 network를 update하는 방법이다.

state value : 현 state에서 가능한 모든 action의 action value 값의 평균
( $V_\pi(s,a)=E_{a\text{\textasciitilde}\pi}[Q_\pi(s,a)]$ ) 이다.

state에 연관된 action 모두에 영향을 줄 수 있다. 자세히 들여다보자. Dueling DQN을 위해선 advantage의 개념이 추가된다.

$A_\pi(s,a)=Q_\pi(s,a)-V_\pi(s)$

Advantage function은 Q-function에서 state value를 빼 해당 action a의 중요성에 대한 지표이다.

  advantage값이 큰 action은 해당 action value가 state value (policy $\pi$ 에서 현재 state s 에서 가능한 모든 action에 대한 action value의 평균) 보다 크다는 것을 의미한다.
  action a가 다른 action value보다 더 큰 return값을 가진다고 해석할 수 있다. 현 상태에서 가능한 모든 action의 advantage에 대한 평균은 0이다.

$E_{a\text{\textasciitilde}\pi}[A_\pi(s,a)]= E[Q_\pi(s,a)]-E[V_\pi(s)]=V_\pi(s)-V_\pi(s)=0$

• value function V : 특정 state s에 대한 value
• Q-function : 특정 state s에서 action a를 선택할 시 얻는 value
• advantage function : 특정 state s에서 선택할 수 있는 모든 action에 대한 각 상대적인 value

policy $\pi$ 가 제일 큰 Q값만을 선택하는 policy라면, $a*=argmax_aQ(s,a)$ 일때

$Q(s,a*)=V(s)$ 이다. $A(s,a*)=0$ 이다. 왜냐하면, action value와 state value가 같아지기 때문이다. (return제일 큰 action만 선택해서 평균 내도 action value와 동일함)

$Q(s,a;\theta,\alpha,\beta)=V(s;\theta,\beta)+A(s,a;\theta,\alpha)$

$\theta:$ parameter of convolutional layers

$\alpha,\beta:$ parameters of two streams(state,advantage) of fully-connected layers.

위의 수식을 통해 max Q값을 가지는 action을 선택하게끔 policy를 update하게 된다.

---

하지만, 위의 수식은 Q 값에 대해 V(state value)가 영향을 많이 미친지, A(advantage)가 영향을 많이 미친지 알 수 없다. 같은 Q값에 대해서 수많은 case가 존재하는 것이다. 이를 Q로부터의 V와 A를 unidentifiable하다고 한다. 즉 식별을 해낼 수, 도출해낼 수 없는 것이다. 여기서 advantage function의 특징을 활용해 제약조건을 추가한다.

advantage function : 특정 state s에서 선택할 수 있는 모든 action에 대한 각 상대적인 value

Q value 즉, action value가 가장 큰 action이면 advantage value 또한, 가장 큰 값임을 확인 할 수 있다. 해당 조건을 활용해 수식을 수정한다.

$Q(s,a;\theta,\alpha,\beta)=V(s;\theta,\beta)+A(s,a;\theta,\alpha)-max_{a'\in|action_{space}|}A(s,a;\theta,\alpha)$

위의 수식에서 max Q값을 return하는 action a*을 선택하게 되면,

$Q(s,a*;\theta,\alpha,\beta)=V(s;\theta,\beta)+A(s,a*;\theta,\alpha)-max_{a'\in|action_{space}|}A(s,a;\theta,\alpha)$ 이 되고,

$A(s,a*;\theta,\alpha)-max_{a'\in|action_{space}|}A(s,a;\theta,\alpha)=0$ 이기 때문에,

$Q(s,a*;\theta,\alpha,\beta)=V(s;\theta,\beta)$ 이 된다.

즉, $V(s;\theta,\beta)$ 은 value function의 estimate를 제공하고, 다른 stream은 advantage function의 estimate를 생성하게 된다. stability를 위해서 실제로 적용되는 Dueling DQN은 average를 사용한다.

$Q(s,a;\theta,\alpha,\beta)=V(s;\theta,\beta)+( A(s,a;\theta,\alpha)-\frac{1}{|action_{space}|} A(s,a;\theta,\alpha))$