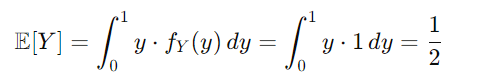NN<9> GAN에 대한 수식 증명

김동한·2024년 8월 16일

Nerual Network

목록 보기

10/10

GAN이란?

GAN(Generative Adversarial Networks)은 새로운 데이터를 생성하는 머신러닝 프레임워크의 한 종류이다. 위조 데이터를 생성하는 Generator network와 데이터의 위조여부를 판단하는 Discriminator network로 이루어져있다. 각 네트워크는 서로 반대되는 Task를 가지고 있다. 서로 더 잘 속이기 위해, 더 잘 구별하기 위해 학습을 진행하여 최종적으로, Generator가 진짜같은 데이터를 생성해내는 것을 목표로한다. 이미지 데이터를 생성하는 것을 기준으로 GAN에 대해 알아보자!

Generator, Discriminator의 수학적 역할(Distribution)

우리가 눈으로 보는 image는 사실 하나의 행렬 및 분포라고 볼 수 있다. 기본적으로, image의 한 pixel마다 0~255의 값을 가지고 있고 여러 pixel들로 이루어진 한개의 image는 특정 분포를 이룬다고 할 수 있다. GAN은 바로 이 개념에서부터 시작한다. 바로, Image는 여러 feature들의 distribution으로 이루어져있다는 것이다.

이전의 위조데이터를 생성하는 Generator는 바꿔말하면, 실제 데이터와 유사한 distribution을 갖는 가짜 데이터를 생성하는 임무를 수행하게 되는 것이다. Noise로 이루어진 분포를 입력으로 받아 실제 데이터와 유사한 distribution을 생성해내는 것이 바로 Generator의 역할이다.

그렇다면, Discriminator도 수학적으로 설명이 가능해진다. Generator가 생성한 위조 distribution을 보고, 실제로 존재하는 이미지인지, 생성된 이미지인지를 판별해내는 것이 Discriminator의 역할이다.

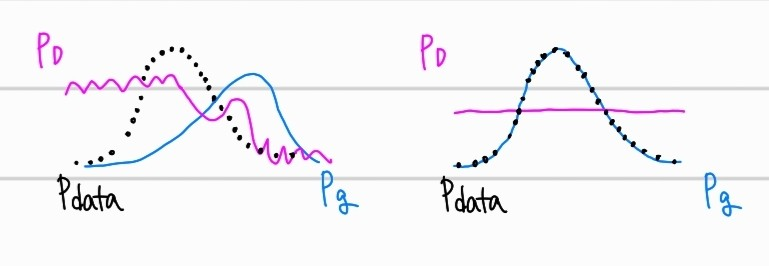
위의 그림과 같이 표현 가능하다. $P_{data}$ 는 실제 이미지의 분포, $P_g$ 는 생성된 가짜 이미지의 분포, $P_D$ 는 discriminator가 예측하게 되는 확률분포를 의미한다. 좌측의 그래프와 같이 학습 초기에는, 가짜 이미지에 대한 판단이 쉽지만, 우측 그래프와 같이 최종적으로 GAN 모델이 학습된 상황에서는, Discriminator가 원본과 가짜를 구별하지 못해 $\frac 1 2$ 의 예측 확률을 보여주게 된다.

Loss function

GAN은 독특한 손실함수를 가진다. 서로 적대적인 임무를 위해 학습하는 네트워크이기 때문에, min max game을 통해 성능 향상을 이룬다. 손실함수는 아래와 같다.

\min_G \max_D V(D, G) = \mathbb{E}_{x \sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]

각각 G(Generator)는 최소화를 위해서 학습하고, D(Discriminator)는 최대화를 위해서 학습한다. 여기서 어디를 최대, 최소화 하나면? 바로 log안의 값을 최대,최소화 하려고 학습을 진행한다. 먼저, 우변에 있는 두개의 항에 대해서 의미를 파악해보자

실제 데이터를 실제 데이터로 판별할 확률

\mathbb{E}_{x \sim p_{data}(x)}[\log D(x)]

D (Discriminator)는 input에 대해서, 실제 데이터라고 판단하면, 1의 값을 그리고 가짜 데이터라고 판단하면, 0의 값을 output으로 가지는 함수다. 이때 첫번째 항은, 실제 데이터에 대해서 실제 데이터라고 예측할 확률에 log를 취한 평균이다. Discriminator가 실제 데이터에 대해서 잘 예측할 수록 더 높은 값을 반환하게 된다. 즉, 실제 데이터에 대한 예측성능을 나타내는 지표이다.

가짜 데이터를 가짜 데이터로 판별할 확률

\mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]

두번째 항은, 가짜 데이터에 대해서 가짜 데이터라고 예측할 확률에 log를 취한 평균이다. 먼저, G(Generator)는 noise 분포에 해당하는 z에서 어떠한 이미지 분포를 생성해 낸다. 이는 $G(z)$ 에 해당한다. 또한, $1-D(G(z))$ 는 생성해 낸 가짜 이미지에 대해서, 가짜라고 판별한 확률이다. 왜냐하면, D는 input 데이터에 대해서 얼마나 진짜 같은 확률을 가지는 지 output으로 나타내기 때문이다.

이제, 각 항에 대해서 의미를 알게 되었으니, minimize하는 것과 maximize하는 것에 대해서 살펴보자

Maximize Discriminator

Discriminator는 실제 데이터도 실제 데이터로 잘 예측하고, 가짜 데이터도 가짜 데이터로 잘 예측해야한다. 이는 각각 첫번재 항과 두번째 항에서의 값을 의미한다.

실제 데이터에 대한 예측 성능이 높다 → $D(x)$ 값이 높다 ( $x$ 는 실제 데이터 분포)
가짜 데이터에 대한 예측 성능이 높다 → $D(G(z))$ 값이 작다 ( $G(z)$ 는 가짜로 생성한 데이터 분포)

따라서, 두 $log$ 값이 커질 수록 Discriminator는 좋은 방향으로 학습되는 것이다.

Minimize Generator

Generator는 D가 가짜 데이터에 대해서 1(실제 데이터)로 예측하게끔 학습하는 것이 목표다. 따라서, 이는 두번째 항의 $D(G(z))$ 를 크게 만드는 것이 목표라는 것을 알 수 있다. 최종적으로, $\log(1 - D(G(z)))$ 에 해당하는 부분이 최소화 되는 것이다. ( $1-D(G(z))$ 가 작아지니까)

이제 마지막으로, Discriminator가 최대값을 가질 때, Generator가 만든 distribution이 실제 distribution과 일치하게 된다는 것을 증명해보자. 이부분은 꽤 어려운 수학이 포함되어있을 수 있다. ~~그리고, 손글씨라서 악필양해를 바란다.~~

Global Optimality

Discriminator의 Optimal point (max point)

위의 전제가 성립한다는 것을 증명할 것이다. 먼저, 손실함수부터 접근해보자. 평균을 확률분포가 주어진 상태기 때문에 아래와 같이 정리할 수 있다.

그리고, 노이즈 분포 Z에서 생성한 데이터분포에서의 평균은, 노이즈 분포 Z의 평균과 동일하다. 물론 확률분포는, $p_z(z)$ 에서 $p_g(x)$ 가 된다. 이는 $x=G(z)$ 과정에서 매핑되어 연결된다는 것을 알 수 있다.

정리해서, Generator 자체가 애초에, 노이즈를 받아 데이터 도메인으로 변환하는 함수이기 때문에, $x=G(z)$ 로 매핑이 가능하고, z 도메인에서의 기대값 계산은 사실상 x 데이터 도메인에서의 기대값 계산과 동일하다는 것을 알 수 있다. 간단한 예시로 생각해보자.

예시 문제 상황) X는 [0,1]에서 균일하게 분포하는 확률변수다. 확률밀도함수는 따라서 $f_X(x)=1$ 이다. 여기서, 새로운 확률변수 Y를 Y=X로 정의해보자. Y는 X에서 어떤 변환된 변수이다.

X 의 평균은 위와 같이 계산된다.

Y의 평균은 위와 같이 계산된다. 따로, 확률 밀도함수가 변하지 않았기 때문에 $f_Y(y)=f_X(x)$ 로 평균은 같은 $\frac 1 2$ 이다. GAN에서도 마찬가지이다. 물론 확률 밀도함수를 $p_z(z)$ 에서 $p_g(x)$ 로 변환해야 하지만, 평균은 동일하다는 것이다.

최종적으로 아래와 같이 수식이 정리된다.

이는 아래와 같은 log 꼴로 생성되고 최종적으로 최초의 전제가 성립함을 알 수 있다.

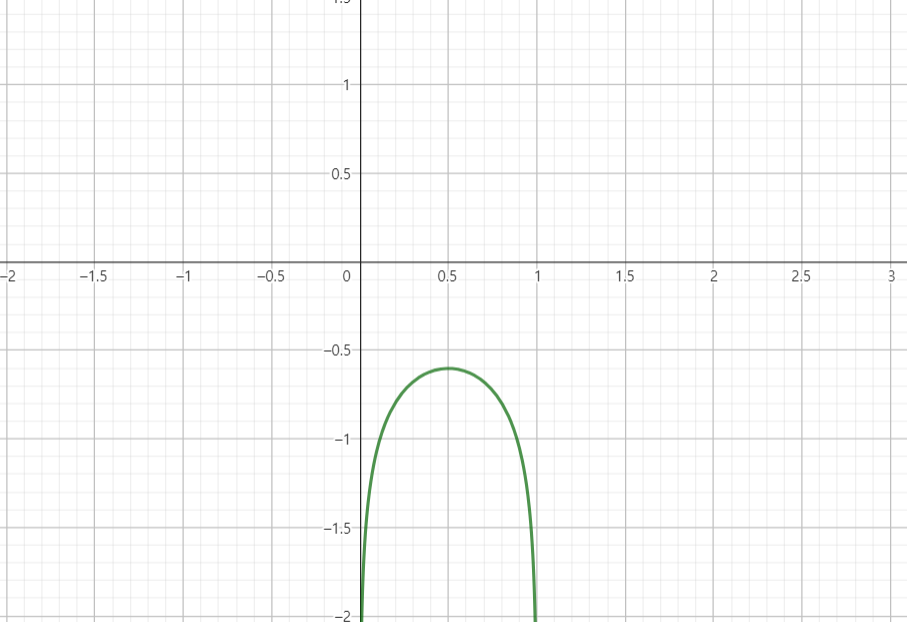
참고용으로 log(x)+log(1-x) 그래프는 이와 같이 생겼다. 최대 점이 되는 point가 해당 전제의 point라는 것을 알 수 있다. 아니면 그냥 미분하고 극점을 찾아도 상관은 없다.

D의 Optimal point일때 $p_g=p_{data}$ 이다.

최종적으로, 우리의 목표인 Generator는 max인 Discriminator를 가정하였을 때, $p_g=p_data$ 일때 최소값을 가지며, 이는 $-log4$ 라는 것을 알 수 있다. 마찬가지로 증명을 해보자.
먼저 C라는 함수를 maximize된 Discriminator일때의 loss function으로 정의하자.

C(G)=\max_DV(G,D)

먼저 loss수식에서 Discriminator를 바로 최대일때의 point로 치환하는 것이 가능하다.

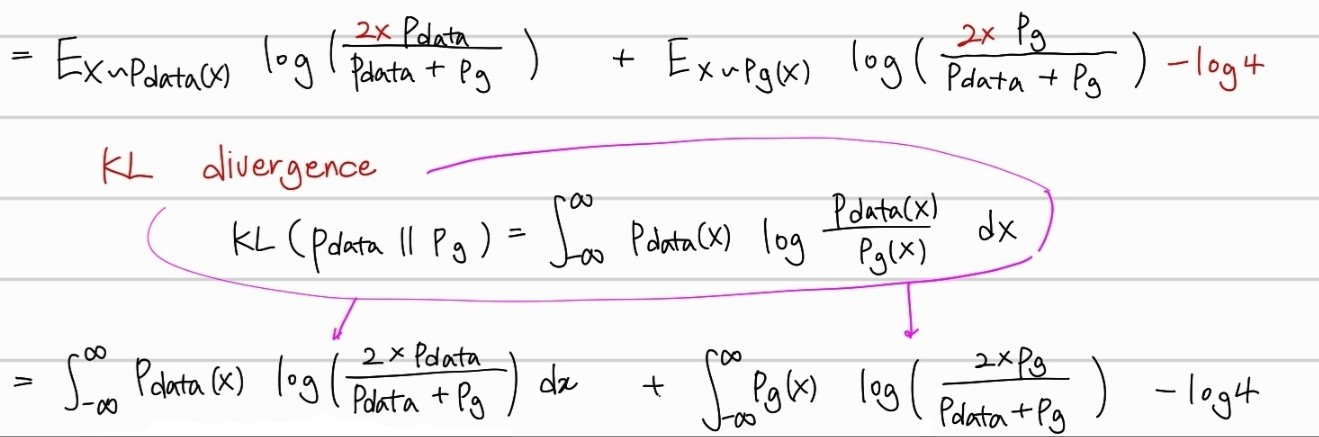
그 이후, KL Divergence를 적용한 후에, JS divergence를 적용하면,

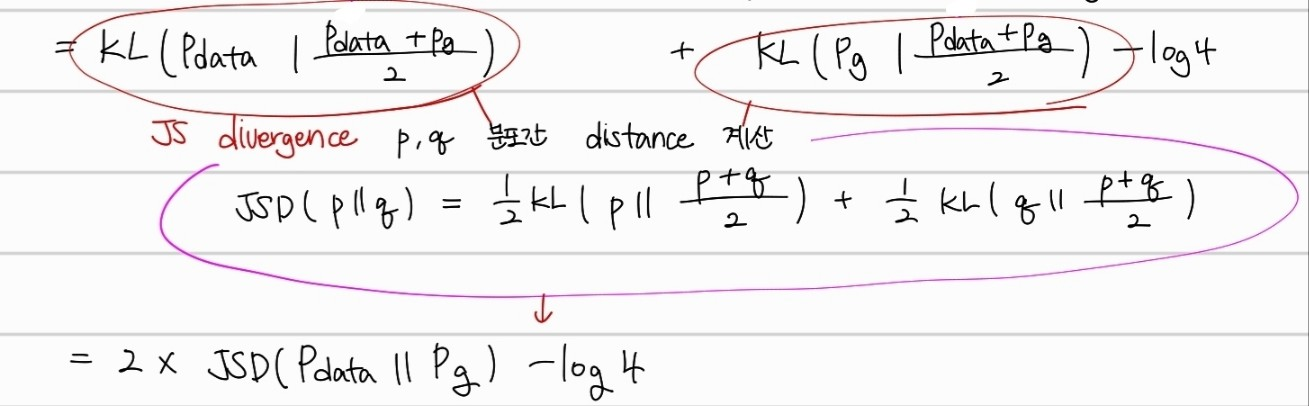
위와 같이 최종 수식이 도달된다. JSD는 두 확률분포의 distance를 측정하는 함수라고 생각하면 편하다. 두 확률분포가 가까울 수록 0을 output으로 가진다. 최종적으로 $P_{data}$ 와 $P_g$ 가 동일한 분포를 가질 때, $-\log 4$ 라는 최솟값을 가지는 것을 확인할 수 있었다.