PCA(Principle Component Analysis)

김동한·2024년 9월 28일

Math in ML/DL

목록 보기

5/5

PCA

PCA란 고차원 데이터를 작은 차원으로 축소해 데이터의 주된 패턴을 파악하는 데 사용하는 차원 축소 기법이다. 쉽게 생각해서 데이터셋에 존재하는 변수의 수를 줄이는 것이다. 변수의 수를 줄이고 간결하게 표현하는 이유는 뭘까?

차원의 저주

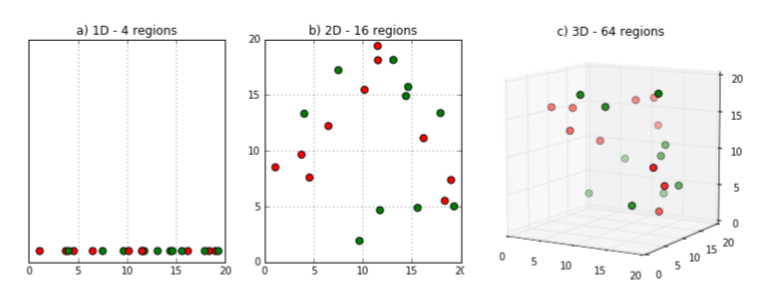
차원의 저주는 데이터의 차원이 높아질 수록 알고리즘 실행이 까다로워진다는 것을 의미한다. 차원(변수)가 증가하게 되면 공간의 부피가 너무 빨리 증가하기 때문에 사용 가능한 데이터가 적어진다는 것이다.

변수의 수가 실제 데이터의 양을 고려했을때, 너무 많으면 위와 같이 데이터 간 거리가 점점 멀어진다. 정보가 없는 불필요한 공간을 많이 학습한 모델의 성능이 떨어지는 원리이다.

PCA 주 목적

차원 축소 :

데이터의 복잡성을 줄여서 시각화가 쉽고 계산량을 줄이고 차원의저주를 해결하는 도움을 준다.

특성 추출 :

데이터의 중요한 패턴을 파악하고, 주 성분이라고 불리는 새로운 특성으로 표현해 노이즈나 상관관계가 높은 데이터를 제거해야한다. 최대한 서로 관계가 적은 독립적인 주요한 변수들로 구성할 수 있께끔 해야한다.

데이터 압축 :

데이터의 정보를 가능한 많이 유지하면서, 더 작은 크기의 데이터로 변환할 수 있어야 한다.

이의 핵심 원리는 데이터의 분산을 최대화하는 주성분을 찾는 것이다. 데이터 분포에서의 분산은 데이터가 얼마나 특정한 방향으로 퍼져있는지를 나타낸다. 분산이 크면, 데이터의 주요정보나 패턴이 포함된 것을 의미한다. (분산이 크면 분포의 폭이 넓어진다고 보면됨)

주성분의 수는 PCA의 하이퍼 파라미터로 설정되고, 목표로 하는 차원의 수를 의미하게 된다. 주성분 값에 맞게끔 차원의 수를 줄이는 것으로, 최종적으로 계산 효율성 증가, 데이터 시각화에서의 이점, 노이즈 제거와 과적합 방지가 가능해진다.

PCA 직관적인 해석

먼저, PCA는 앞서 말한것과 같이 차원을 축소하는 것이다.

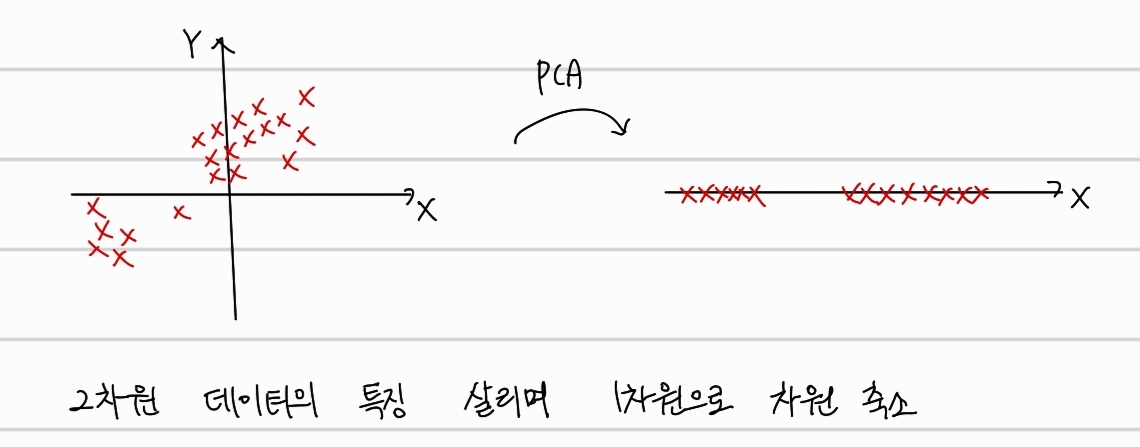
간단한 예시로 위와같이 2차원의 데이터를 1차원으로 축소하는 과정에서 최대한 분포의 특징을 살리면서 축소하는 것을 PCA라고 한다. PCA는 아래의 과정으로 진행된다.

Step1.

각 축에 대한 평균값을 구하고, 평균이 원점이 될 수 있게 shift한다.

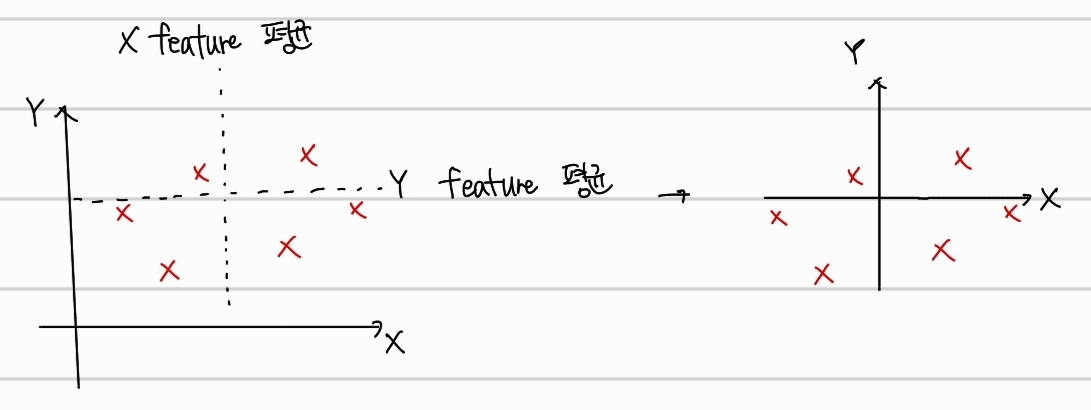
Step2.

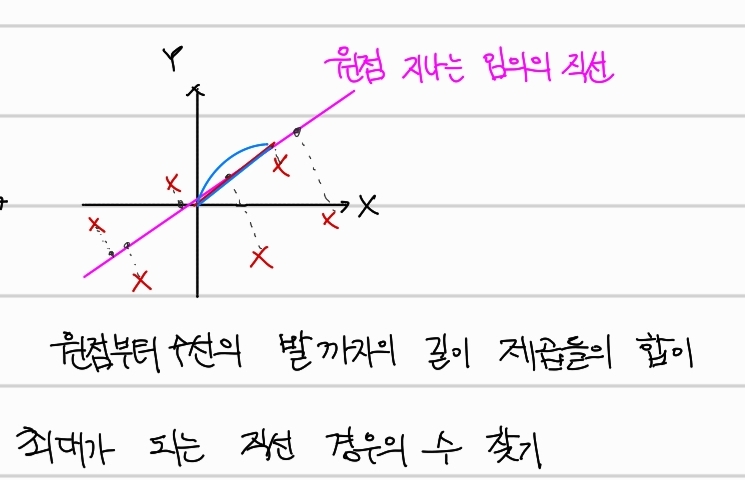원점을 지나는 임의의 직선을 그린다. 그 후, 각 데이터에서 그 직선까지의 수선의 발을 내리고, 원점부터 수선의 발까지의 길이를 구한다. 여기서 구한 길이의 제곱들의 합이 최대가 되는 직선을 찾는다.

Step3.

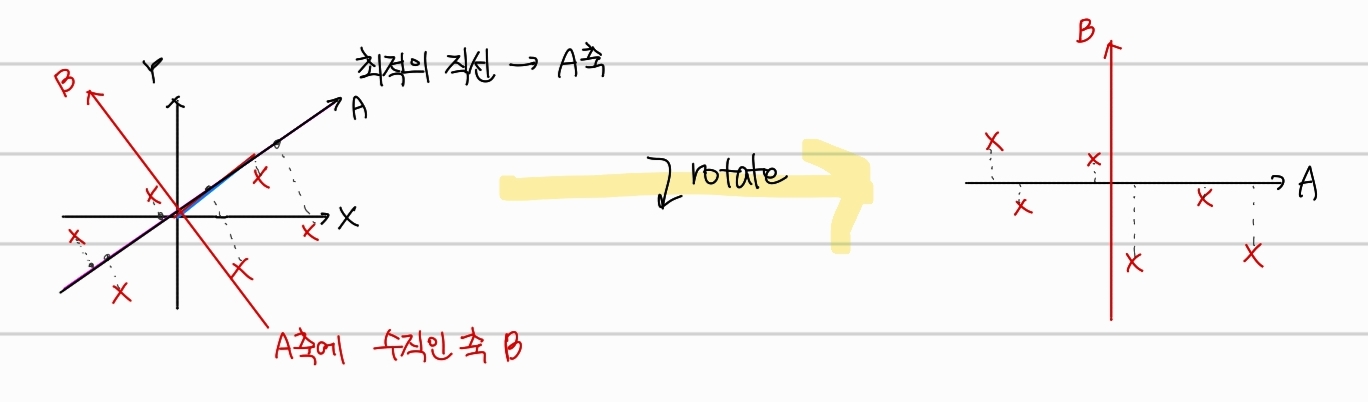
찾은 최적의 직선의 방향을 가리키는 vector를 바로 eigenvector라고 하고 이때 x축 길이와 y축 길이의 비율을 loading score라고 한다.

Step4.

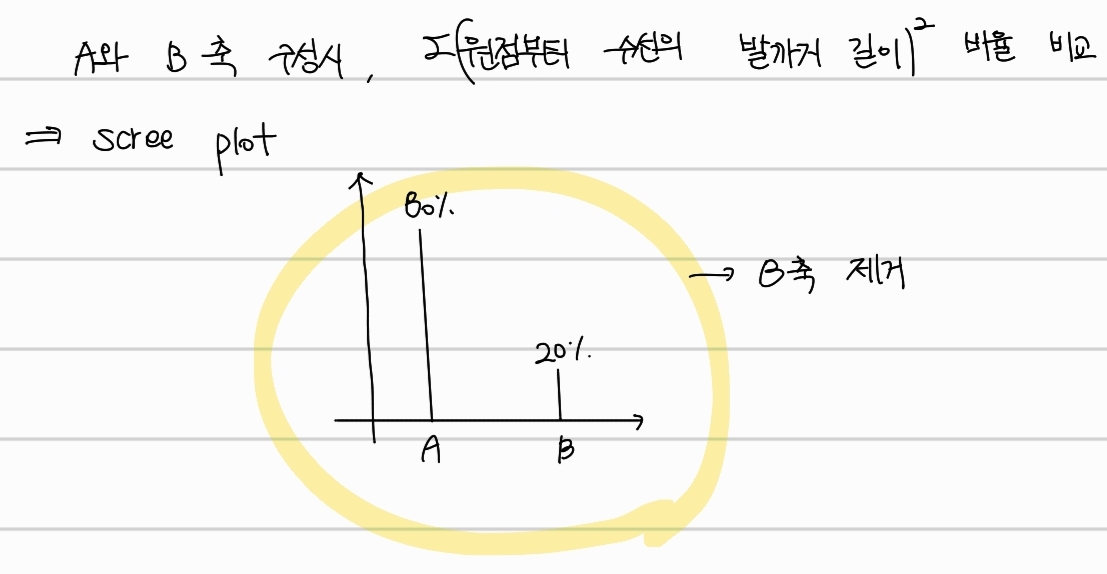마지막으로, 해당 축과 수직한 축을 구해 새로운 축들을 x,y축이 되도록 회전시키면 각 축이 얼마나 잘 표현하고 있는지 나타내주는 scree plot을 그릴 수 있다. 이는 A와 B축을 구성할 때 원점부터 수선의발 까지의 길이의 제곱합 간 비율로 구할 수 있다. 위를 통해 B축을 제거하면 어느정도 특성을 지킨 채 차원감소를할 수 있다는 것을 알 수 있다.

PCA 수학적인 해석

먼저 covariance와 eigenvector 등 기본 배경에 대해서 다뤄보자.

Variance

제일 먼저, variance는 편차 제곱의 평균이다.

(X-m)^2

위와 같은 편차의 제곱을 풀어서 작성하면,

X^2-2Xm+m^2

이 된다. 이에 대해 평균을 구하면,

E(X^2)-2{E(X)}^2+{E(X)}^2 \newline = E(X^2)-E(X)^2

이 바로 variance다. variance는 데이터의 퍼진 정도를 나타낸다. 더 많이 퍼질 수록 더 큰 값을 가진다.

Covariance

covariance는 2차원 이상의 고차원 데이터들 간의 variance이다.

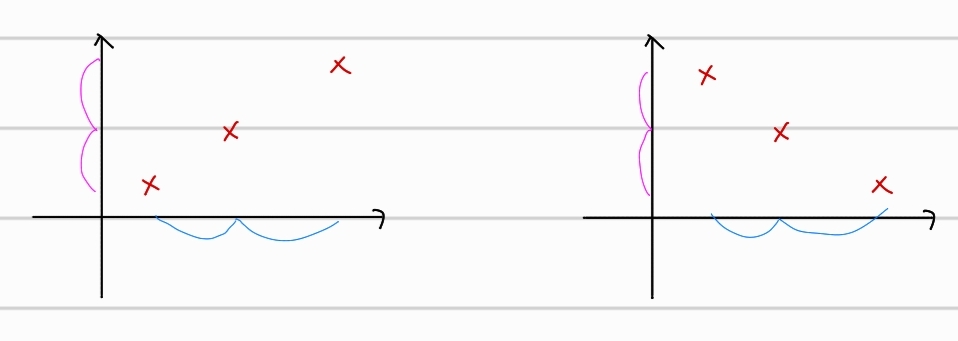
위의 두 분포는 x축 기준에서의 variance와 y축 기준에서의 variance가 동일하다. 따라서, 두 축에 대한 각 분포의 variance를 마냥 더하면, 서로 다른 분포임에도, 같은 covariance를 가질 수 도있다. 따라서 다음과 같이 covariance를 구한다.

Cov(X,Y)=\frac 1 n \sum_{i=1}^n(X_i-\mu_X)(Y_i-\mu_Y)

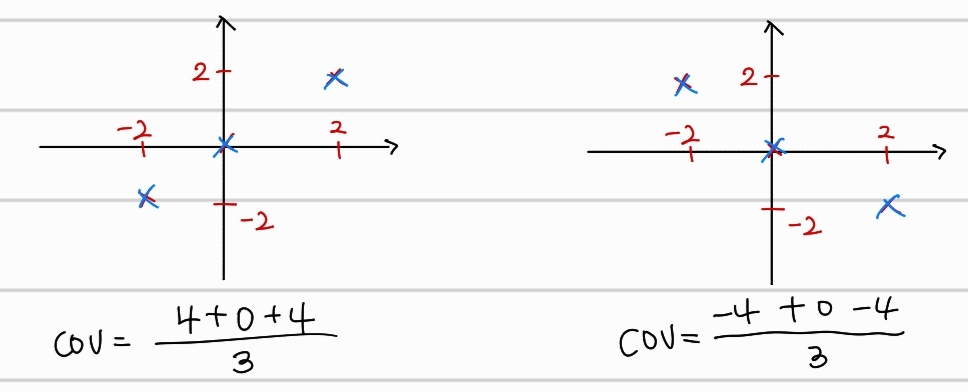결론적으로 서로 다른 분포에 대해서는 다른 covariance를 구할 수 있다. 여기서 x축과 y축의 평균이 모두 0이어야 한다.

Covariance matrix

이전에 구한 covariance를 통해 covariance matrix 행렬을 만들 수 있다. 2차원 데이터에서의 covariance matrix는 아래와 같다.

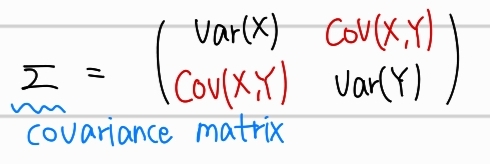
이 행렬은 주 대각선을 축으로 대칭인 symmetric한 형태이다

shearing

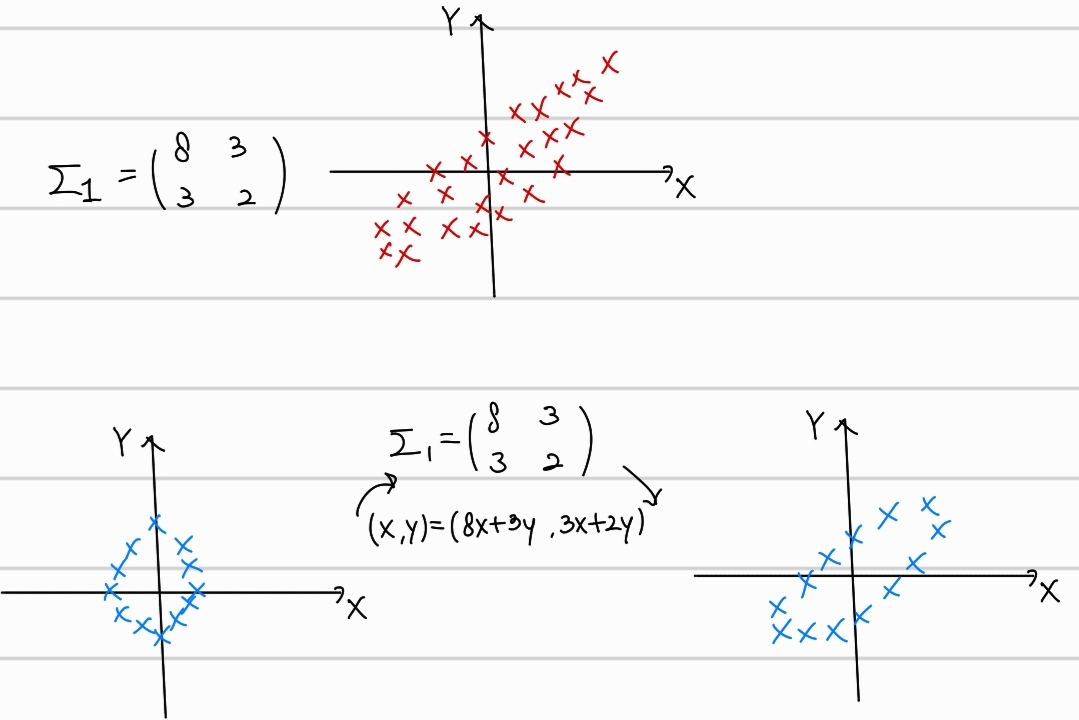
위의 그림을 보면, covariance matrix로 선형변환을 진행했을 때, covariance matrix의 특성에 맞게, 데이터의 분포가 변형되었다. 이를 shearing이라고 한다.

Eigenvector, Eigenvalue

eigenvector는 행렬 A에 의한 선형변환이 이루어졌을때, 변환의 전후 벡터가 가리키는 방향이 일정한 벡터를 의미한다.

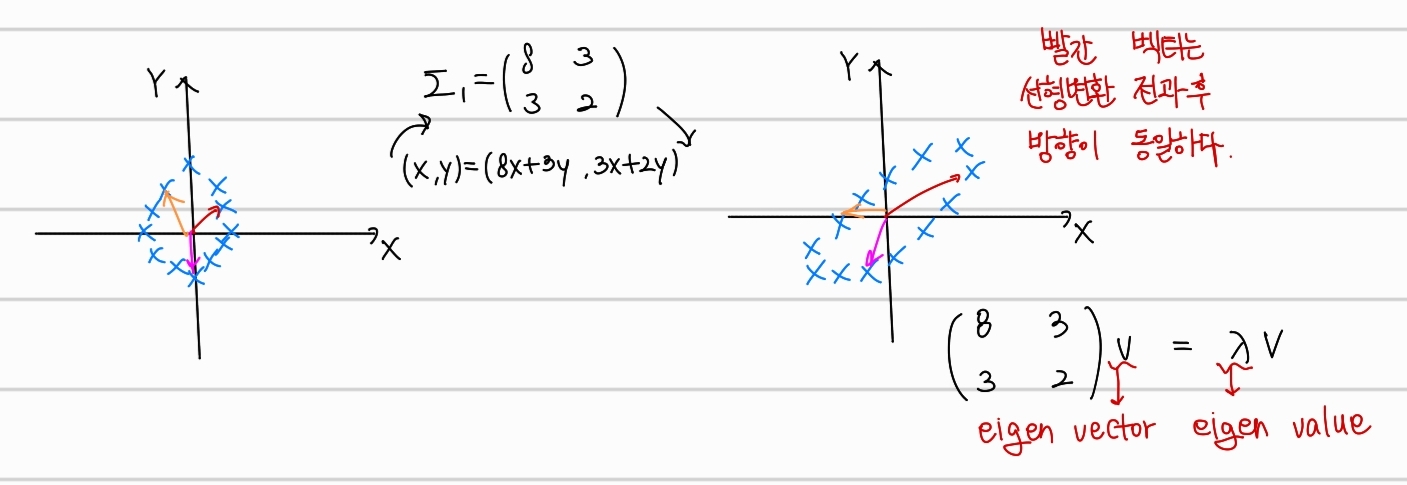
예를들어 이전 shearing의 결과를 벡터와함께 그렸다고 가정하였을 때, 위와 같은 결과가 나왔을때 빨간 vector가 바로 eigenvector이다. 수식은 우측 하단에 작성한것처럼 매우 단순하다. eigenvector를 만족하는 길이 비율의 값인 $\lambda$ 가 바로 eigenvalue이다.