최소 제곱법 (최소자승법)

predict값과 target값의 차이(잔차)의 제곱합을 최소화하는 매개변수 W와 b를 추정하는 방법이다. 쉽게 생각하면, 주어진 데이터를 좌표위에 점을 찍고난 후 그 점과 내가 그을 직선사이의 거리가 최소화되는 직선을 구하는 방법이다.

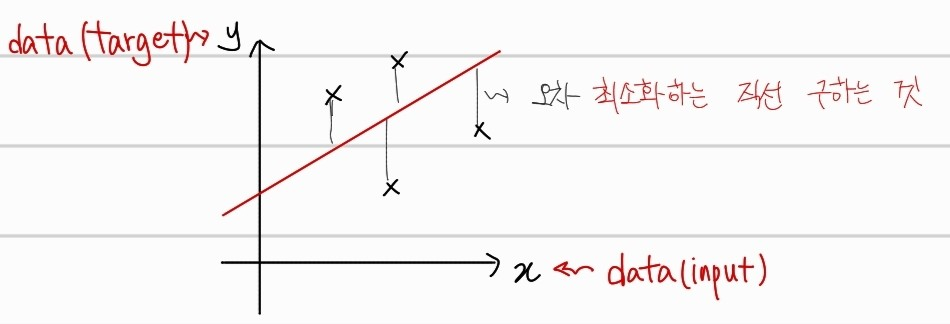
위와 같이 빨간 직선으로 선형식을 예측한 후, 실제 값인 (X) 포인트들과의 거리를 최소화 할 수 있도록, 직선의 기울기를 회전하거나, 위아래로 평행 이동하는 것이다. 손실함수는 아래와 같다. 이를 행렬로 변환하여, 가중치(선형계수)에 해당하는 W와 b를 구해보자.

Loss 최소화하는 W와 b

먼저 위의 그래프에서의 직선과, target 점을 수식으로 나타내보자.

graph 수식은 간단하게 직선의 방정식을 나타낸다. 여기서, 실제 data input ($x_i$) 에 대한 예측값은 $\hat y_i$ 로 나타냈다. 그냥 data input x에서의 직선의 방정식 위에서의 점을 의미한다. 또한, target인 y값과의 오차를 제곱하여 모두 더한 것을 최소 제곱합이라고 한다. 이를 미분하는 과정을 통해서, 극값을 구해서 $E$를 최소화하는 변수에 해당하는 $W$ 와 $b$의 값을 구할 것이다.

---

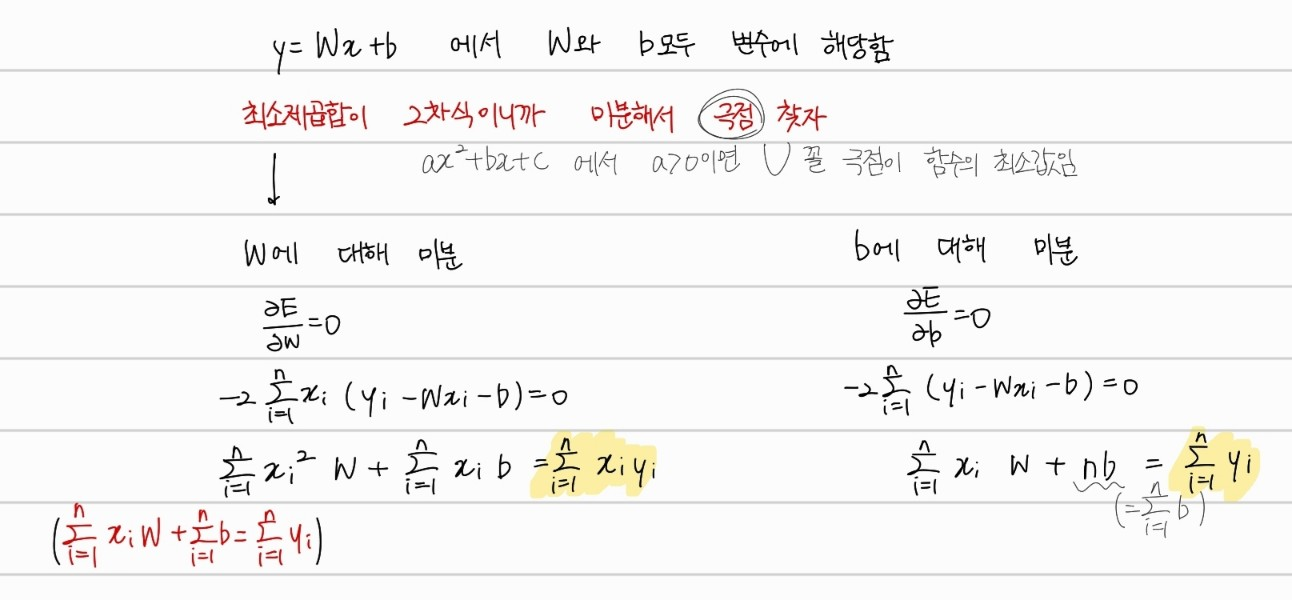먼저 변수에 해당하는 $W$와 $b$에 대해서 $E$를 미분해보자. 그러면 위의 과정과 같이 노란색으로 하이라이트한 수식 두개가 연립방정식으로 세워진다. 물론, 위의 수식을 그대로 풀이해도 상관없지만, 행렬로 나타내서 더 쉽게 표현을 해보자.

---

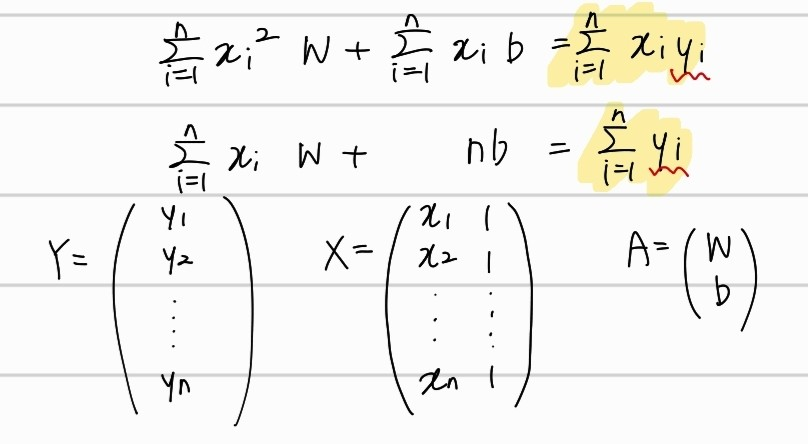위와 같이, 행렬 $Y$, $X$, $A$ 로 위의 연립방정식으로 표현해보자. 그 이후 $A$에 대해서 정리하면, Error를 최소화하는 $W$와$b$로 이루어진 행렬 $A$를 구할 수 있다. 먼저 좌변부터 행렬로 표현해보자.

좌변은 위와 같이 행렬로 표현할 수 있다. 마찬가지로 우변도 행렬로 표현하면

이처럼 표현 가능하다. 마지막으로, A에 대해서 위의 수식을 모두 정리하면,

선형회귀 과정에서 오류를 최소화하는 계수 조합 A 행렬에 대한 수식을 표현 가능하다.

간단한 코드

넘파이로 weight를 표현하면 아래와 같이 표현 가능하다. 마지막으로 증명된 수식을 그대로 numpy로 표현한 것 뿐이다. linalg.inv는 역행렬을 구하는 메서드이다.

self.weights = np.array(np.linalg.inv(X.T@X)@X.T@y)

Reference

https://ko.wikipedia.org/wiki/%EC%B5%9C%EC%86%8C%EC%A0%9C%EA%B3%B1%EB%B2%95
https://subprofessor.tistory.com/104