후위표기법
우리가 일상생활에서 흔히 사용하는 숫자 사이에 연산자를 넣는 식을 중위표기법이라고 한다. ex) 와 같은 경우가 있다. 후위표기법은 컴퓨터가 연산을 하기 쉽게 수식을 표현하는 것으로 연산자가 피연산자의 뒤에 위치한다. 앞선 예시를 후위표기법으로 표현하면, ex) 가 된다. 후위표기법으로 변환하는 규칙은 다음과 같다.
규칙
- 피연산자인 숫자는 그대로 출력한다.
- Stack이 비어있으면 push한다.
- Stack의 top 연산자의 우선순위 < 지금 연산자 우선순위 → push
- Stack의 top 연산자의 우선순위 >= 지금 연산자 우선순위 → 3번이나 2번 조건 될때까지 pop하기
- 중위표기식의 끝까지 도달했으면 Stack empty 될때까지 pop
- 여는 괄호는 Stack에 조건없이 push
- 여는 괄호 다음의 연산자는 Stack에 push
- 닫는 괄호 나오면 여는 괄호 나올때까 모두 pop, 괄호는 버림
그림으로 이해하는 것이 더 쉽다.
그림
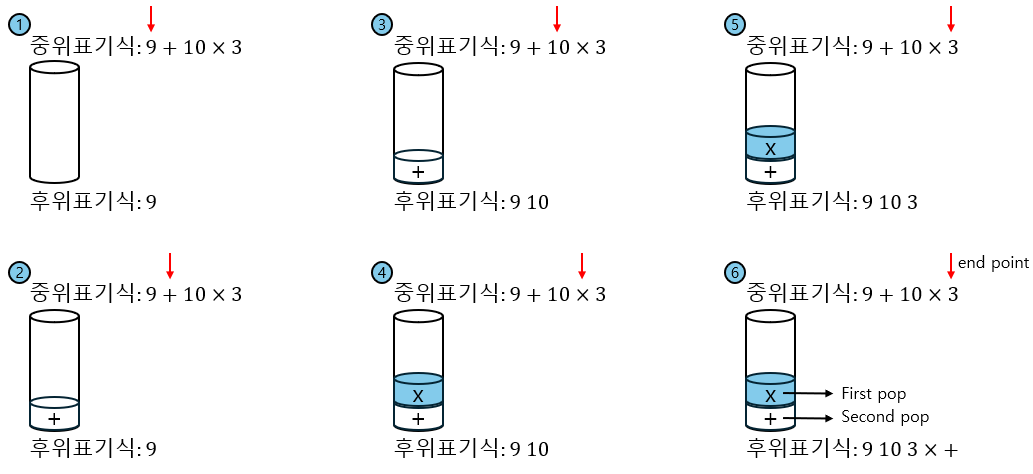
를 후위표기식으로 나타내면 가 된다.
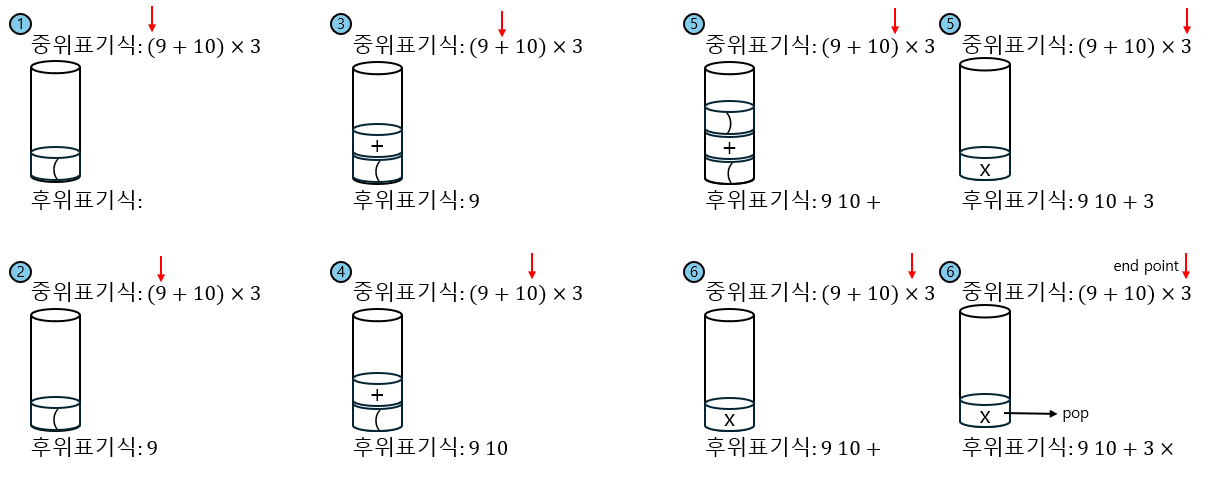
괄호가 있는 경우 '('는 무조건 stack에 push하고 ')' 이 현재 연산자일때, stack의 '('까지의 모든 연산자를 pop하는 과정으로 위의 후위표기식과 다르게 괄호안의 연산을 먼저 하는 것을 알 수 있다.
Stack을 활용한 후위표기법으로 변환
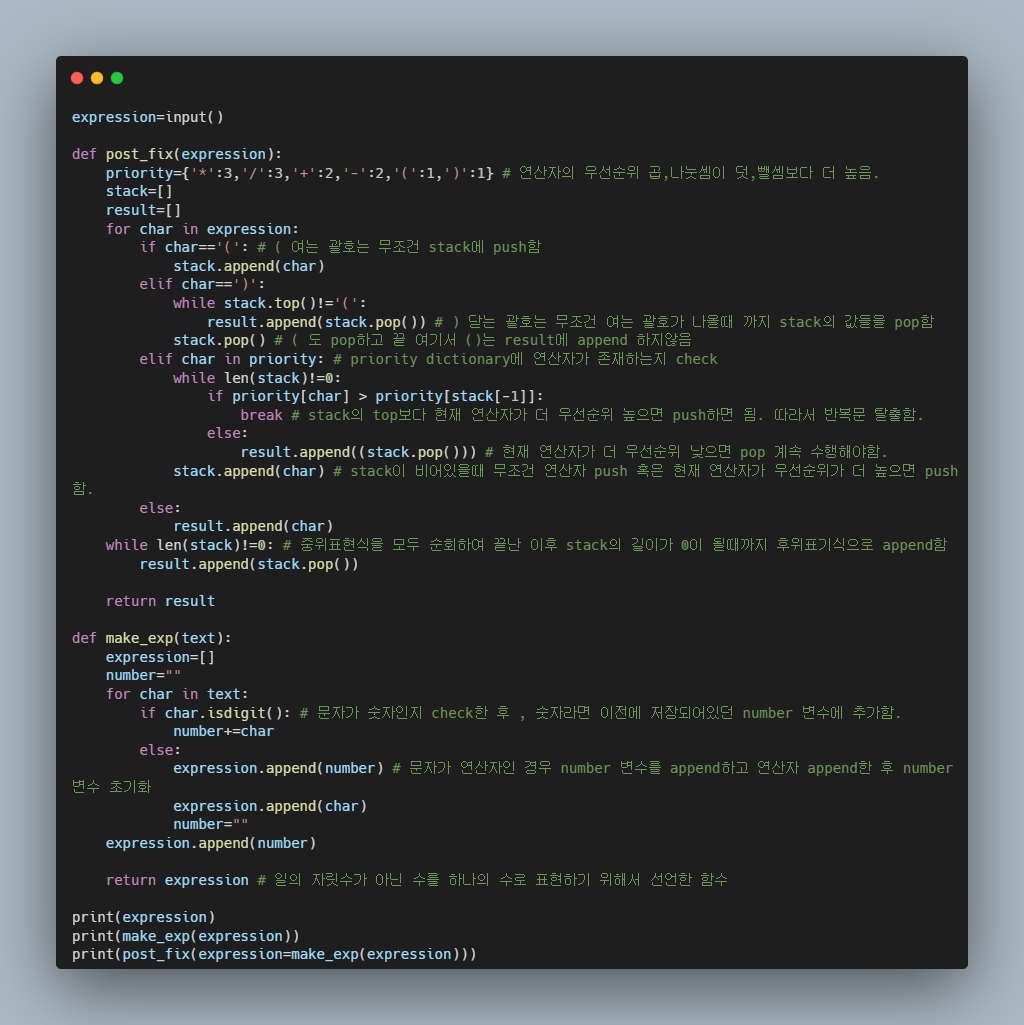

후위 표기법 계산법
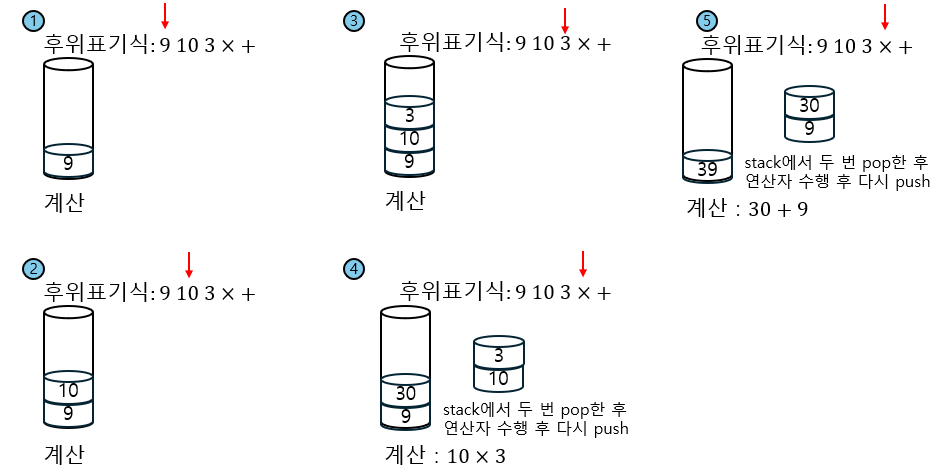
후위표기법으로 변환한 식에서 차례로 숫자는 stack에 push하고 인덱스가 연산자를 가리킬때 stack에서 두번 pop을 진행해 연산을 수행한 후 다시 stack에 push해준다. 이 방법으로 후위표기식의 끝까지 진행했을때 stack에 남아있는 값이 바로 연산의 결과이다.
Stack을 활용한 사칙연산 구현
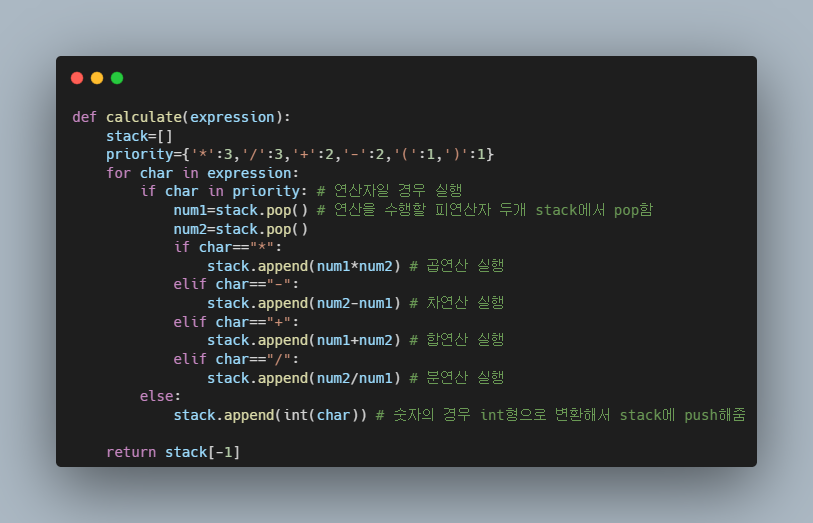
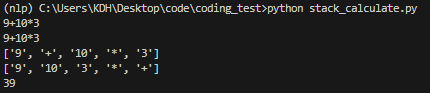
Reference
https://velog.io/@dev_sony503/Python-%EA%B3%84%EC%82%B0%EA%B8%B0-%ED%9B%84%EC%9C%84-%ED%91%9C%EA%B8%B0%EB%B2%95-Stack
https://todaycode.tistory.com/73

