
문제

입력

출력

예시 입출력

풀이
거스름돈을 계산하는 유사한 문제를 풀었던 기억이 있다. 그 문제는 동전의 값어치가 문제에서 주어졌었는데, 이 문제는 동전의 값어치를 입력받기 때문에, 동전간 배수관계를 확인할 수 없다.
따라서, DP로 해당 문제를 접근했다. DP는 큰 문제를 작은 문제로 소분하고, 점화식으로 표현하는 것이 중요하다. 주어진 예시로 수식을 세워보자.
우리가 계산해야하는 값은 총 10원이다. 1원, 2원, 5원으로 10원을 이루는 모든 경우의 수를 계산해야한다. 10원보다 더 작은 수를 합해서 10원을 구성하는 것이 가능하다. ex) 5원의 경우의 수 + 5원의 경우의 수 = 10원의 경우의 수
따라서, 0원부터 10원까지를 이루는데 가능한 경우의 수를 하나씩 구해보자. 예시에선 3가지 동전의 종류가 주어지는데, 1원부터 경우의 수를 계산해보자.
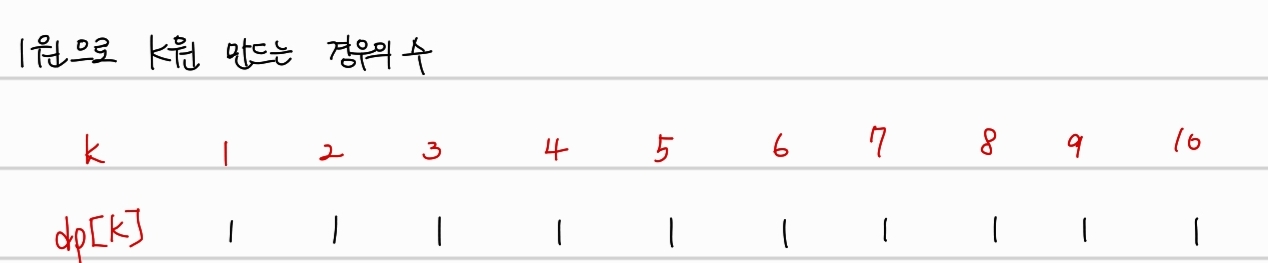
1원으로 k원을 만드는 경우는 모두 다 1가지이다. 전부 1로만 이루어진 경우의 수만 존재한다.
다음으로, 1원과 2원으로 만드는 경우의 수를 계산해보자.
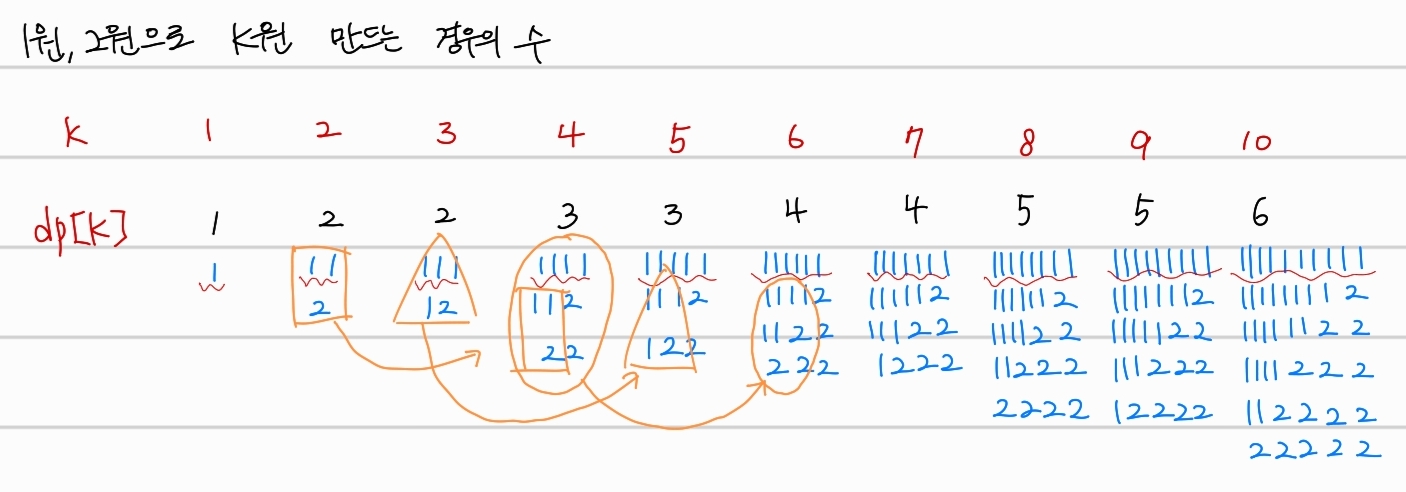
1원과 2원으로 구성하는 경우, 특이한 규칙이 발생한다.
-
모든 경우의 수에 1원으로만 이루어진 경우의 수가 추가 되어있다. (최상단 경우)
-
2원이상부터 "k-2원" 값을 이루는 경우의 수가 추가되는 것을 확인할 수 있다.
- k=2를 이루는 경우
k가 0일때의 경우의 수가 추가됨
- k=3를 이루는 경우
k가 1일때의 경우의 수가 추가됨
- k=4를 이루는 경우
k가 2일때의 경우의 수가 추가됨
...
즉 현재 입력된 coin의 값어치인 a원만큼 빼두고, k-a 원을 이루는 경우의 수를 구하면 된다.
최종적으로, 현재 입력된 coin에서 1원부터 목표 K원까지 각각을 이루는 경우의 수를 구해보면,

위와 같이, 두가지 case를 합한 경우가 된다.

점화식은 위처럼 세울 수 있다.
여기서, 특이 case가 몇가지 있다.
- k가 0일때 (dp[0]=??)
0원을 이루는 경우의 수는 동전 그 어느것도 선택하지 않는 것이기 때문에 딱 1가지 존재한다.
- k-a가 0보다 작아질때
k를 이루는 경우, 우리는 동전을 합하기만 한다. 빼진 않기 때문에, 위의 경우, K는 당연히 입력한 coin 부터 update를 하게 된다. 그 이전의 경우는 차이가 없기 때문이다.
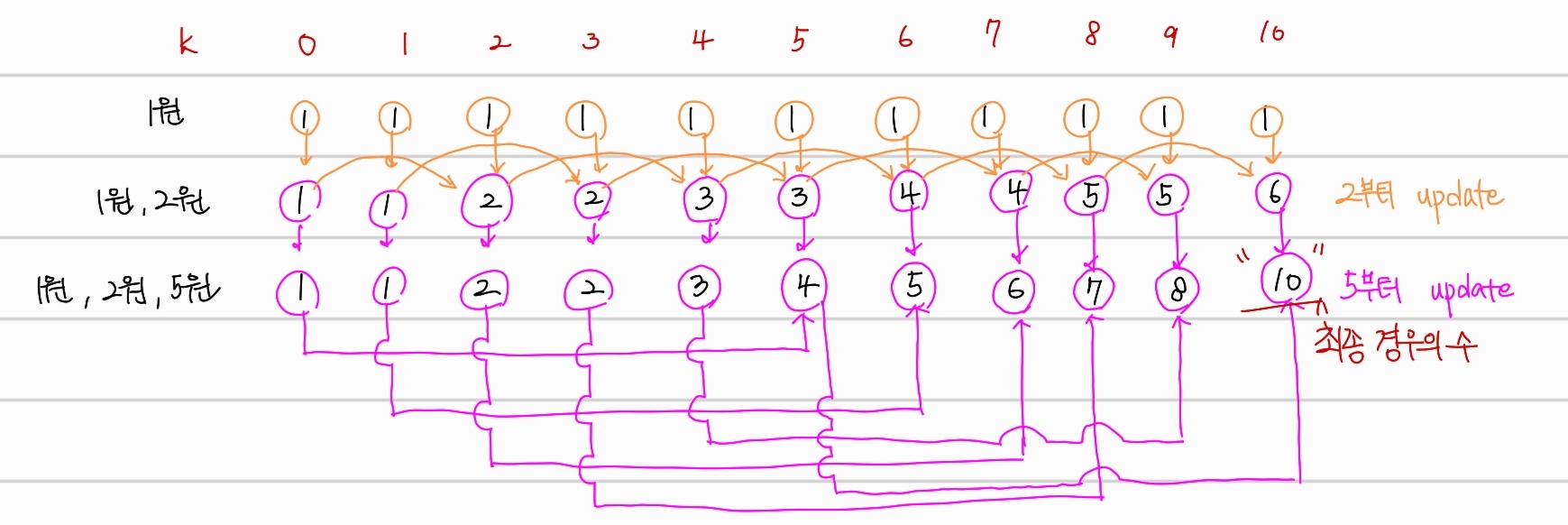
예시의 경우 위의 연산을 거치며 최종적으로 10가지 경우의 수가 존재하게 된다. 확인해보면, 새로 입력된 coin은 해당 coin부터 k까지만 값을 update하는 것을 알 수 있다. 1원,2원,5원 모두 입력되었을때, 5원의 경우 k가 0,1,2,3,4원은 update가 없음을 알 수 있다.
코드
# 동전 1
n,k=map(int,input().split())
DP=[0]*10001
DP[0]=1
for _ in range(n):
coin=int(input())
for j in range(coin,k+1):
DP[j]+=DP[j-coin]
print(DP[k])
